Шта су дигитални потписи и како функционишу?

Дигитални потписи слични су електронским верзијама ваших рукописа. Омогућују људима да провере аутентичност и интегритет података, као и спречавање потписника у могућности да одбаци (негира) своје учешће.

Ова својства довела су до усвајања дигиталног потписа у широком спектру апликација, укључујући многе наше безбедносне протоколе, сигурну е-пошту и у управљању дигиталним правима.

У овом чланку ћемо говорити шта су дигитални потписи, где се користе, као и техничке детаље два најпопуларнија алгоритма, РСА и ДСА.

Шта су дигитални потписи?

Као што је горе наведено, дигитални потписи дају нам три врло важна својства. То су аутентификација, интегритет и непотврђивање.

Аутентикација је поступак провере да ли је појединац који пошаље поруку заиста онај за кога кажу да је, а не преварант.

Тхе интегритет података или поруке односи се на то да ли је стигао у истом стању као када је послан. Ако је порука измењена или измењена, она више не задржава свој интегритет.

Ако су подаци или порука не може се одбити, то значи да се њен аутор не може оспорити да су били прави ствараоци документа. Ова некретнина одузима вјероватну порицање или стари изговор “Извини, мој пријатељ је користио мој рачун”.

Све док приватни кључ појединца није угрожен, дигитални потписи могу све ове три особине давати подацима.

Можда се питате зашто су нам ова имања потребна у првом реду. Идемо корак уназад и размислимо о томе како радимо ствари у сусрету лицем у лице.

Рецимо да дугујете свом пријатељу Микеу 100 УСД. Добра си особа, па му драго кад му вратиш новац кад добијеш новац.

Најбољи начин да то учините био би само дати Микеу новчаницу од 100 УСД. Познавали сте га годинама и знате како изгледа, тако би и било лако је потврдити његов идентитет и на тај начин потврдити да новац дајете правој особи.

Ако сте заиста анални, чак бисте могли да проверите његову личну карту и натерате га да потписује руком писани рачун за вас. Потпис на примитку дао би му интегритет и учинио га не поновљивим.

Шта ако ако не извршите трансакцију лицем у лице, добијете позив од некога ко каже да је то Мике и да бисте морали да пошаљете 100 УСД на број рачуна 12345678.

„Али не звучиш као Мике“, кажеш.

“Прехлађена сам. Пошаљите га сада, треба ми новац. “

Хоћете ли послати новац? Вероватно не.

Нема шансе да се зна да ли је заиста Мике или тачан број рачуна. Колико знате, то би могао бити преварант који покушава да вам украде. Уместо да новац одмах пребаците, било би најбоље да сачекате док не угледате Микеа како бисте му новац могли дати лично.

Баш као у горњем сценарију, често наилазимо на ситуације у којима то морамо верификовати идентитет странке или интегритет података у он-лине свету. Због тога су дигитални потписи постали механизам који може пружити ове особине и олакшати сигурне мрежне трансакције.

Без њих можда не знамо са ким разговарамо, не бисмо могли да будемо сигурни да ли су подаци били фалсификовани или не, и особа би могла да негира да су одговорни..

Употреба дигиталног потписа

Ова својства дигиталног потписа чине их корисним у широкој употреби. Они се често користе сами или заједно са енкрипцијом у различитим безбедносним протоколима, као што су:

• ИПсец
• ССХ
• ТЛС

Они се такође често користе у управљање дигиталним правима, ин блоцкцхаин технологија, ин управљање уговорима апликација, као део дистрибуција софтвера, а у финансије.

Историја дигиталног потписа

Идеју о дигиталном потпису први су пласирали познати криптографи Вхитфиелд Диффие и Мартин Хеллман у свом раду из 1976. године Нови правци у криптографији. 1978. Роналд Ривест, Ади Схамир и Лен Адлеман су у јавност погледали алгоритам РСА, који се може користити за производњу несигурних дигиталних потписа.

Прошла је још једна деценија да се дигитални потписи појаве у широкој апликацији: издању ИБМ-овог Лотус Нотес 1.0. Од тада па надаље, дигитални потписи су почели да се шире како би се појавиле нове технике и појачале потребе за интернетском аутентификацијом и провером интегритета..

Кратки увод у криптографију са јавним кључем

Пре него што ускочимо у дигитални потпис, најбоље је покрити неке од важних аспеката криптографије јавног кључа, који чине основу за рад дигиталног потписа.

Ако сте релативно нови у криптографији, систем који ћете највише упознати је шифрирање кључа симетричног кључа. То само значи да се исти шифар (који је сличан лозинци, али има неке разлике) користи и за шифровање и за дешифровање података.

Шифрирање по јавном кључу била је револуција, јер је укључивала користећи одвојене кључеве за процес шифровања и дешифровања, што доводи до низа различитих криптографских апликација. Ова два кључа формирала су пар кључева, који се састоји од јавног и приватног кључа. Јавни кључ се очигледно може јавно делити, док приватни кључ мора бити тајан да би систем био безбедан.

Две најчешће употребе криптографије с јавним кључем су шифрирање и дигитални потпис.

Шифровање

Једна од револуционарних карактеристика криптографије јавног кључа била је та омогућава странкама које се никада нису среле да поверљиво шаљу поруке једна другој. Пошиљалац тражи јавни кључ жељеног примаоца (они се могу наћи на серверима јавних кључева, на личним веб локацијама или једноставно тако што ће појединац затражити), а затим шифрује поруку овим кључем, пре него што га пошаље примаоцу..

Прималац је једина особа којој може приступити порука – под претпоставком да приватни кључ није угрожен – дешифрујући је својим приватним кључем. Иако се за шифрирање поруке користио јавни кључ, он се може дешифровати само приватним кључем. Ако прималац жели да одговори, они ће пронаћи јавни кључ оригиналног пошиљаоца, а затим поновити поступак.

Погледајте такође: Објашњени су уобичајени типови шифрирања

Како функционишу дигитални потписи?

Као што смо рекли, дигитални потписи користе се за аутентификацију, да се види да ли су подаци били неовлаштени и да би се омогућило непотврђивање. Постоји низ различитих механизама који се могу користити за дигитални потпис, и сваки од њих има мале варијације у начину структурирања.

Опћенито, ови алгоритми морају бити састављени од три под алгоритма:

• Алгоритам генерирања кључева – Овај алгоритам генерише случајни пар кључева за корисника. Бројеви укључени у пар кључева морају се придржавати одређених параметара да би се сматрали сигурним. Два најважнија аспекта су та да су бројеви довољно случајни и одговарајуће величине.
• Алгоритам за потписивање података – Једном када корисник има своје кључеве, постоје одређени начини на који ће се начин применити на податке у процесу потписа.
• Алгоритам за верификацију потписа – Исто тако, верификација потписа следи унапред одређени поступак.

Да би систем дигиталног потписа био ефикасан, он мора бити структуриран на такав начин да:

• Подаци потписани приватним кључем су потврђено одговарајућим јавним кључем истог појединца.
• Било би у суштини немогуће (користећи тренутну технологију и технике) кривотворити важећи потпис без познавања приватног кључа појединца.

Неке од најчешћих схема дигиталног потписа укључују РСА, ДСА, ЕцДСА и ЕдДСА.

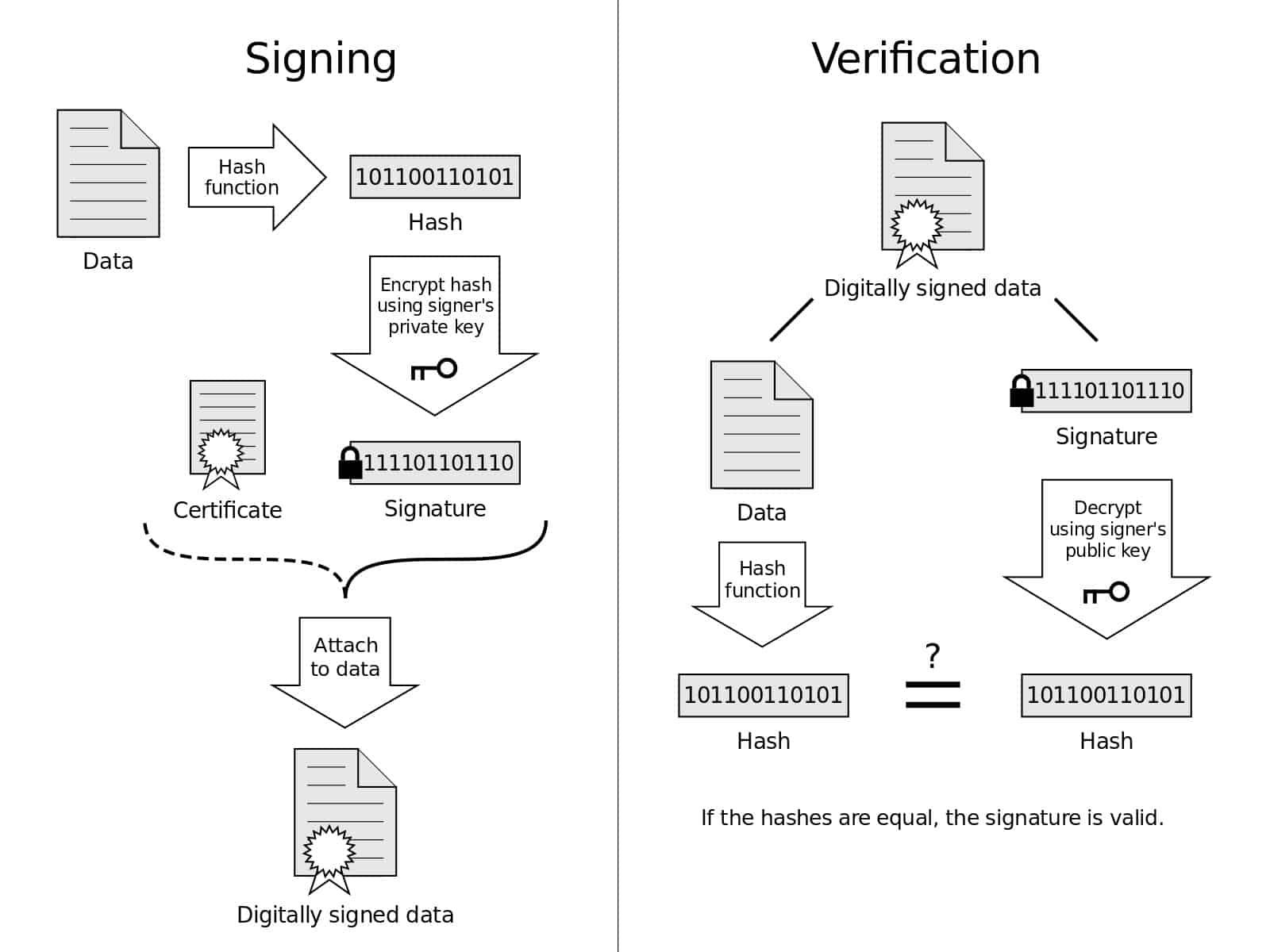
Ова слика даје визуелни приказ процеса потписивања и верификације. Дијаграм дигиталног потписа од стране Ацдк под лиценцом под ЦЦ0

РСА

РСА је први алгоритам дигиталног потписа, али се такође може користити за шифровање јавним кључем. У овом ћемо чланку прескочити аспект шифрирања, али више о томе можете сазнати у нашем свеобухватном чланку који покрива шта је РСА и како функционише..

РСА кључна генерација

У сигурним имплементацијама РСА, парови кључева ће се обично успоставити аутоматски у следећем процесу:

Приме генерација

Бирају се два појединачна главна броја, п и к. Тачна величина ових примера варираће овисно о величини кључа. Ових дана се за адекватну сигурност генерално препоручује најмање 2048-битни РСА тастери, па говоримо о два главна броја који се множе да би се створио 2048-битни број.

2048 бита је величина у систему бинарних бројева. Ако би број ове величине био претворен у познатији децимални систем, то би био отприлике овако дугачак:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Примери у РСА морају бити изабрани насумично и морају имати сличне дужине.

У нашем примеру користићемо много мање бројеве да бисмо ствари лакше разумели. Имајте на уму да би коришћење тастера ове величине учинило да дигитални потписи буду лажни. Због тога се тако велике вредности користе у пракси.

Рецимо то:

п = 13

к = 17

Први корак би био да се израчуна модул н користећи следећу формулу:

н = пк

н = 13 к 17

н = 221

Вредност н је такође дужина кључа.

Цармицхаелова тотиентна функција

Сада када имамо вредност за н, следећи корак је употреба Цармицхаелове тотиентне функције:

λ(н) = лцм (п – 1, к – 1)

Неколико је ствари које морате да схватите:

• λ(н) значи Цармицхаелов тотиент за вредност од н
• лцм представља најнижи заједнички множитељ. Ово је најнижи заједнички број који су обоје п-1 и к-1 могу да се поделе

Укључимо наше податке у једначину:

λ(221) = лцм (13 – 1, 17 – 1)

λ(221) = лцм (12, 16)

Ако сте добри у менталној математици, можда сте то схватили 48 је најнижи заједнички мултипликатор оба 12 и 16. То је зато што је 48 најмањи број у који се могу уклопити оба ова броја (12 к 4 = 48, 16 к 3 = 48). Стога:

λ(221) = 48

Долазим са јавним кључем

У РСА-у, јавни кључ се састоји од вредности н (што смо већ израчунали као 221) и е. Будући да се јавни кључ слободно дели, вредност за е не мора да буде тајна У ствари се у пракси често поставља на 65.537, јер би већи број успорио процес шифровања. У нашем примеру, поставићемо е до 5, само да би био мали и једноставан број за рад.

Стога се јавни кључ за овај пример састоји од 221 и 5. У следећим одељцима објавићемо специфичности примене јавног кључа.

Откривање приватног кључа

Баш као што је наш јавни кључ састављен од два броја, тако је и наш приватни кључ. Приватни кључеви се састоје од д и е. Већ знамо вредност е (5), и ми можемо да користимо следећу формулу за проналажење д:

д = 1 /е мод λ(н)

Напоменути да мод само симболише модул операцију, што би обично значило да ћете морати да пронађете остатак када леву страну поделите на десну. Као пример:

17 мод 3 = 2

То је зато што се 3 уклапају у 17 укупно 5 пута, а остатак је 2.

Наш пример је мало другачији. Тхе “1 /е мод“Чини се да се сегмент једначине може рећи да поделите 1 би е, али заправо није. Збуњујуће је, али ово је начин репрезентације модуларни инверзни. Једначина нам заправо говори да израчунамо модуларни инверзни е и λ(н).

Модуларни инверзни се обично добија употребом проширеног Еуклидовог алгоритма, али то нећемо обухватити у овом чланку. Уместо тога, само ћемо користити интернетски калкулатор да бисмо олакшали ствари.

Сада када смо то извукли напоље, унесемо наше вредности у формулу:

д = 1/5 мод 48

Да пронађем д, све што морамо да урадимо је да унесемо нашу вредност е (5) у мрежни калкулатор где пише цијели број, онда је наша вредност за λ(н), која је 48, где пише модуло.

То нам даје резултат 29 према он-лине калкулатору. Стога ће наш приватни кључ бити састављен од:

е = 5

д = 29.

Сада када смо генерисали оба наша кључа, следеће питање је: „Шта да радимо са њима?“ Па, могли бисмо их користити за шифровање и дешифровање порука путем криптографије јавног кључа, али овај чланак говори о дигиталном потпису, тако да фокусираћемо се на то.

Дигитално потписивање података са РСА

Рецимо да неко жели да пошаље поруку свом пријатељу, али жели да буде сигуран да пријатељ може да провери аутентичност и интегритет поруке. То би могли учинити користећи дигитални потпис РСА за потпис поруке.

Први корак је покрените читаву поруку преко хасх функције. Ово су једносмерне функције које увек дају исти излаз за дани улаз. Сигурне хасх функције у основи је немогуће преокренути, што значи да се излаз не може користити за утврђивање улаза. Такође је немогуће да две одвојене поруке имају исти излаз.

Више о функцијама хасх-а можете сазнати у менију Шта је хешинг? Одељак нашег чланка, Шифрирање, хеширање, сољење – у чему је разлика?

Рецимо да желимо да дигитално потпишемо поруку „Вруће је данас“Тако да наш прималац може знати да ли је порука аутентична или не и да ли је у њој неовлаштено варана. Па бисмо трчали „Вруће је данас“Кроз хасх функцију.

Разумевање хасх функција

Ових дана најчешће се користи заштићени хасх функција СХА-256. Када нашу поруку пребацимо преко интернетског калкулатора СХА-256, она даје резултат као што је овај:

ефбцф22б4цд04д49даа87цфбда7д2313цц665ц35бц9е18954аф16ц104а731952

Ово ствара неколико проблема за наш пример. Први је да то није децимални број као онај на који је већина људи навикла. Можда сте приметили да у овом броју постоје слова и да се само појављују ф. То нам даје појма да је уствари хексадецимални број.

Тхе хексадецимални систем се ослања на базу 16, а не на базу 10, попут система бројева који иначе користимо. То значи да се уместо бројања у множини од 10 броји у множини 16, а првих 6 слова нашег абецеде користе се за израду тих додатних бројева. Број попут овог може се претворити у наш свакодневни децимални систем, али то је ван оквира овог чланка.

Друго питање које имамо је да је то заиста велики број. Ако би се претворио у децимални износ био би још дужи. Будући да смо у овом водичу циљани на једноставност, покретање израчуна с тако великим бројем би учинило превише збуњујућим да би се добили основни концепти преко.

Са идејом да покажемо како РСА дигитални потписи делују на једноставан начин за разумевање, нећемо користити тако велику хасх вредност у следећем примеру. Уместо тога, претвараћемо се да је хеш вредност „Вруће је данас“Је једноставно 10.

Такође ћемо се морати претварати да ће, попут било којег правог хасх-а, сваки пут када ставимо свој унос „Данас је вруће“ преко хасх функције, увек враћати вредност 10. Да бисмо били у складу с начином на који хаш функције нормално раде, мораћемо да се претварамо да је невероватно да било који други улаз даје исту вредност. Слично томе, морамо се претварати да такође није изводљиво сазнати наш изворни унос из ове вредности. Ова својства су оно што чини хешеве изузетно корисним.

Како се приватни кључ пошиљаоца користи за дигитално потписивање хасх вредности

Наш пошиљалац је уписао њихову поруку, а затим је ставио кроз хасх функцију, за коју претварамо да је вратила вредност 10. Једном када пошиљалац има хасх поруке, он може креирати дигитални потпис применом приватног кључа на хасх вредност са следећом формулом:

м (ц) = цд мод н

Ово је заправо формула за дешифровање података који су шифровани јавним кључем примаоца, али се такође користе за дигитално потписивање докумената.

Када је у питању дигитални потпис:

• Вредност м (ц) биће потпис.
• Вредност ц је хасх поруке (10).
• Вредност д је део приватног кључа пошиљаоца, који смо добили раније (29).
• Тхе мод функција је иста преостала операција коју смо претходно покрили.
• Вредност н је други део приватног кључа пошиљаоца, који смо израчунали на почетку (221).

Па, ставимо то све у нашу формулу:

м (ц) = 1029 мод 221

    м (ц) = 100.000.000.000.000.000.000.000.000 мод 221

Покренимо ово помоћу следећег модула калкулатора (објаснили смо како ове операције раде под Откривање јавног кључа одељак). Да би правилно функционисало, морамо да поставимо своје улоге као:

• Број а тип – децималан
• Број а вредност – 100000000000000000000000000000
• Број б тип – децималан
• Број б вредност – 221
• Једнаџба израчунавања (ово је само код који календару говори која операција треба да обавља. Овај и други кодови могу се наћи на веб страници повезаној изнад уноса) – мод (а, б)

Ако сте ствари исправно урадили, требало би изгледати овако:

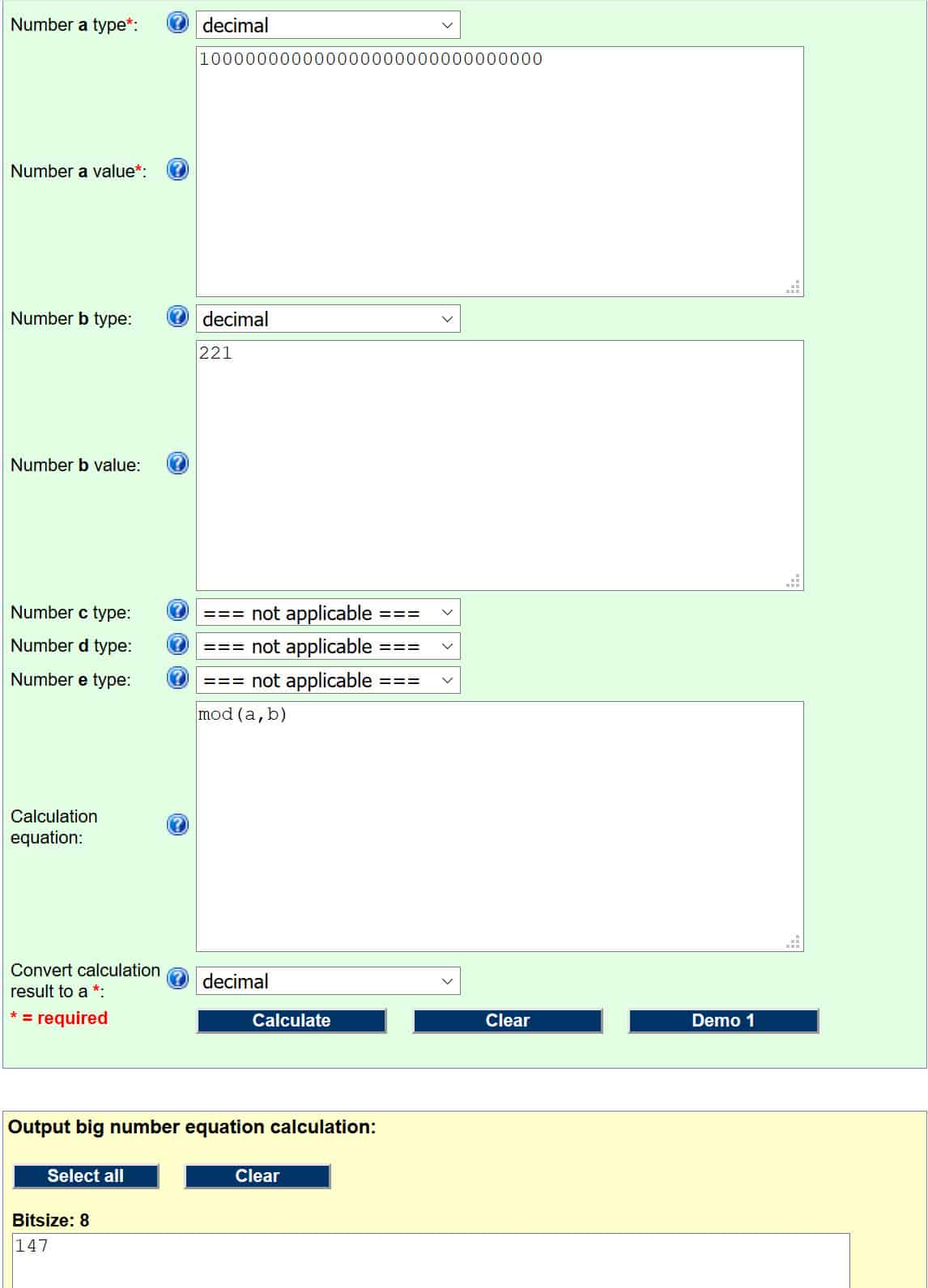
Број у жутом пољу је наш одговор, тако да је дигитални потпис за хасх поруке 147.

Да би доказао аутентичност и интегритет поруке, заједно са пружањем неодбацивања, наш пошиљалац ће поруку пренети „Вруће је данас“Поред дигиталног потписа компаније 147 жељеном примаоцу. Сјетите се само да смо користили малу вриједност за хасх да бисмо поједноставили ствари, умјесто правог хасх-а поруке.

Верификација дигиталних потписа

Дигитални потписи су корисни само ако можемо проверити да ли су легитимни. Све док приватни кључ пошиљаоца није угрожен, прималац може тестирати да ли је порука аутентична и задржава ли свој интегритет применом следеће формуле на дигитални потпис:

    центиметар) = ме мод н

У преокрету процеса потписивања, ово је заправо формула која се користи за шифровање података у РСА. Када користимо ову формулу за верификацију потписа:

• Вредност центиметар) ће бити хасх вредност пошиљаоца у тренутку када су га потписали (због структуре алгоритма РСА јавног кључа, применом пошиљаочевог јавног кључа кроз ову формулу поништиће се операција потписивања коју смо управо извели, оставивши нас са својим оригиналним хасх претварачем ).
• Вредност м је дигитални потпис (147).
• Вредност е је део јавног кључа пошиљаоца, који смо раније сазнали (5).
• Тхе мод функција је иста преостала операција коју смо претходно покрили.
• Вредност н је други део јавног кључа пошиљаоца, који смо израчунали на почетку (221).

Хајде да све то бацимо у формулу:

    центиметар) = 1475 мод 221

    центиметар) = 68.641.485.507 мод 221

Користимо исти модулски калкулатор као и претходно и задржите све исто, осим:

• Број а вредност – 68,641,485,507

Ако сте исправно унели ствари, требало би да добијете резултат:

центиметар) = 10

Сада, када је прималац израчунао вредност хасх-а из дигиталног потписа, њихов следећи корак је израчунавање хасх вредности поруке коју је примио, “Вруће је данас“. Ако се сећате раније, ми заправо нисмо користили прави СХА-256 хасх поруке, јер би број био превелик и направио пример превише компликованим.

Уместо тога, претварали смо се да нам је хасх функција заправо дала мали број, 10, за наш допринос. Пошто хасх функције увек дају исти резултат за дати унос, када наш прималац постави „Вруће је данас„Кроз нашу имагинарну хасх функцију, они би такође добили вредност 10.

Процес верификације потписа има две вредности. Прва вредност је хасх какав је био када га је пошиљалац дигитално потписао својим приватним кључем. Горе смо израчунали ово користећи јавни кључ пошиљаоца.

Друга вредност је хасх поруке коју је прималац примио. То се израчунава коришћењем исте хасх функције коју је пошиљалац користио да би ставио оригиналну поруку. Ове две вредности се затим упоређују, а ако су вредности исте, онда можемо претпоставити да је порука аутентична, да задржава свој интегритет и да се не може поновити. Наравно, ово претпоставља да приватни кључ пошиљатеља није угрожен.

Пошто је наш пример вратио вредност од 10 за хасх када га је потписао пошиљалац, као и вредност од 10 као хасх поруке која је примљена, можемо претпоставити да је порука, “Вруће је данас” долази од особе која тврди да га је послала и да није измењена од када је послата.

Ако прималац жели да одговори тако да њихов дописник може да потврди њихову поруку на исти начин, цео се поступак понавља, осим што се приватни и јавни кључеви примаоца користе за процесе потписивања и верификације..

Сва ова математика можда вас је збацила са целокупном идејом дигиталног потписа. Не брините, јер имплементације РСА аутоматизују овај процес, тако да не морате крчити ниједан број.

РСА прос & контра

РСА је један од најчешће подржаних и имплементираних алгоритама дигиталног потписа, иако постоји помак ка новијим, ефикаснијим и најсигурнијим алгоритмима као што су ЕЦДСА и ЕдДСА.

У поређењу са ДСА-ом (о коме ћемо говорити у следећем одељку), РСА је бржи у верификацији потписа, али спорији у генерисању. Пошто се потписи обично креирају и верификују више пута, РСА се углавном преферира над ДСА.

ДСА

Сигурност алгоритма дигиталног потписа темељи се на два математичка концепта, дискретном проблему логаритма и неким својствима модуларне експоненције. За неке групе је немогуће израчунати њихове дискретне логаритме тренутним техникама и технологијом.

ДСА генерација кључева

Да бисте генерисали ДСА кључеве, први корак је одабир параметара које група корисника у истом систему може користити за генерисање пара кључева.

Генерирање параметара

• Избор а хасх функција – СХА-256 је најчешћа опција за испуњавање савремених безбедносних захтева.
• Постављање на дужину кључева, Л и Н – Ових дана, Л требало би да буде најмање 2.048 бита Н требало би да буде најмање 256 бита.
• Одлучите се за премијеру, к, то је исте дужине као Н.
• Одаберите премијеру, п, где п-1 је вишеструко од к.
• Изаберите број, г, користећи следећу формулу (где х је произвољни број између 1 и п-1):

г = х(п – 1) /к мод п

Обично су ове вредности веома велике, како би се алгоритам учинио сигурним. Да сачувамо наш пример да није превише тешко израчунати или објаснити, користићемо много мање бројеве који заправо не би били сигурни. Рецимо то:

    к = 5

    п = 11

Да пронађем г, убацујемо наше бројеве у формулу. Користићемо 3 као наша вредност х:

г = 3 (11-1) / 5 мод 11

г = 32 мод 11

г = 9 мод 11

Користићемо исти калкулатор модула као и на Како се приватни кључ пошиљаоца користи за дигитално потписивање хасх вредности одељак. Параметри ће бити исти, осим:

• Број а вредност – 9
• Број б вредност – 11

Ако сте све исправно унели, то ће вам дати резултат г од 9.

Генерирање корисничких кључева

Потом поједини корисници узимају ове параметре и користе их за формирање свог кључног пара:

• Приватни кључ (Икс) је број између 0 и к, коју смо поставили на 5. За наш пример ми ћемо изабрати 2 бити Икс, наш приватни кључ.
• Јавни кључ (и) израчунава се следећом формулом:

    и = гИкс мод п

Стога:

и = 92 мод 11

и = 81 мод 11

Још једном ћемо користити исти калкулатор модула. Параметри ће бити исти, осим:

• Број а вредност – 81
• Број б вредност – 11

Ако сте исправно унели ствари, требало је да добијете резултат и = 4. Јавни кључ је, дакле 4.

Сада када смо генерисали све наше вредности, дозволимо вам да кратко сачекамо. Параметри за систем су:

• п = 11
• к = 5
• г = 9

Наш кључни пар чине:

• Приватни кључ, Икс = 2
• Јавни кључ, и = 4

Дигитално потписивање података помоћу ДСА

Пошиљаоци могу да користе свој ДСА приватни кључ за дигитално потписивање података, што омогућава свом примаоцу да провери је ли порука веродостојна и задржава ли свој интегритет. Такође спречава пошиљаоца да може да одбаци поруку.

Процес потписа почиње генерирањем случајне вриједности к, која је између 1 и к. За овај пример, само бирајмо 3 као наш „случајни“ број, к.

Затим следимо следећу формулу да креирамо појединачни кључ (р) за поруку:

р = (гк мод п) мод к

Убацимо у наше бројеве:

р = (93 мод 11) мод 5

р = (729 мод 11) мод 5

Поново користимо наш модулски калкулатор, улази 729 и 11, што нам даје резултат 3. Стога:

р = 3 мод 5

А онда поново поновимо модул операцију са новим вредностима које ће нам дати:

р = 3

Наша вредност за р користи се као кључ за поруку.

Смислимо други део дигиталног потписа, с, са следећом формулом:

с = к-1(Х(м) + кр) мод к

Тхе к-1 не представља узимање негативне моћи к, али уместо да израчунамо модуларни инверзни, баш као и код нас Откривање потпоглавља приватног кључа у ранијем делу чланка где смо говорили о РСА.

Х(м) је вредност хасх-а за поруку коју пошиљалац потписује. Обично би то била дуга хасх вредност која је изведена из поруке, баш као и у Разумевање хасх вредности пододјељак горе, који смо покривали када смо говорили о РСА алгоритму.

За овај пример, ствари ћемо поједноставити. Баш као у одељку РСА, то ћемо рећи и наша порука, м, је „Вруће је данас“ и да је хасх поруке Х(м), је 10.

Дакле, унесите све наше вредности у формулу:

с = 3-1 (10 + 2 к 3) (мод 5)

с = 3-1 (10 + 6) (мод 5)

с = 3-1 (16) (мод 5)

Сада ћемо узети модуларни обратни облик 3 за наредбу од 5 (јер 5 је наша вредност к), користећи исти модуларни инверзни калкулатор од раније. Унесите 3 као цели број и 5 као модул, који ће вам дати резултат 2. Стога:

с = 2 (16) (мод 5)

с = 32 (мод 5)

Вратимо се нашем калкулатору за нормалан рад модула, задржавајући исте параметре као и раније, осим:

• Број а вредност – 32
• Број б вредност – 5

Ако сте то исправно урадили, добиће вредност за с од 2. Дигитални потпис се састоји од р и с (3 и 2, респективно). Пошиљаоци преносе дигитални потпис примаоцу заједно с њиховом поруком, “Вруће је данас“. Они ће такође делити вредности п, к, г и и са примаоцем.

Верификација дигиталних потписа

Када прималац прими дигитални потпис поред поруке, може да провери интегритет и аутентичност поруке са следећим сетом израчуна.

Први корак је проналазак хасх-а поруке коју су добили. Прималац ово ради покретањем целокупне поруке преко хасх функције. Да би ствари биле једноставне и доследне, рецимо да је хасх поруке, Х(м) је 10.

Примаоцу су такође послате следеће вредности које користе у поступку верификације:

• Дигитални потпис (р, с) – 3, 2
• п – 1
• к – 5
• г – 9
• и – 4

Први израчун је пронаћи в:

в = с-1 мод к

Опет с-1 представља узимање модуларног обрнутог. Унесите наше вредности:

в = 2-1 мод 5

Користићемо модуларни инверзни калкулатор од раније. Унесите 2 као цели број и 5 као модул, који ће вам дати резултат 3 за в. Следећи корак је проналажење у1 са следећом формулом:

у1 = Х(м) Икс в мод к

Убацимо у наше вредности:

у1 = 10 к 3 мод 5

у1 = 30 мод 5

Вратите се уобичајеном калкулатору модула задржавајући исте параметре као и раније, осим:

• Број а вредност – 30
• Број б вредност – 5

То нам даје резултат 0 фор у1.

Следећу формулу користимо у2:

у2 = р Икс в мод к

Унесите наше бројеве:

у2 = 3 к 3 мод 5

у2 = 9 мод 5

Затим се враћамо уобичајеном калкулатору модула користећи исте параметре као и раније, осим:

• Број а вредност – 9
• Број б вредност – 5

Ако ово исправно унесете, добиће резултат за у2 од 4.

Сада када имамо своје вредности за у1 и у2, можемо наћи в, са следећом формулом:

в = (гу1иу2 мод п) мод к

Убацимо у наше бројеве:

в = (90 к 44 мод 11) мод 5

в = (1 к 256 мод 11) мод 5

в = (256 мод 11) мод 5

Вратимо се нашем уобичајеном калкулатору модула користећи исте параметре као и раније, осим:

• Број а вредност – 256
• Број б вредност – 11

То нам даје резултат 3. Стога:

в = 3 мод 5

Тада користимо нормалан калкулатор модула један крајњи пут, опет са истим параметрима, осим:

• Број а вредност – 256
• Број б вредност – 11

То нам даје резултат за в од 3.

Ако је порука веродостојна и није мењана, тада в ће бити једнак р:

    в = 3

    р = 3

    3 = 3

Стога је поруку послао власник приватног кључа, а порука није измењена од потписивања.

ДСА про & контра

Сигурност ДСА се ослања на то да ли користи адекватан број. Додатно п, к и г придржавајући се исправних параметара, вредност к такође мора бити случајна. То не би требало да буде предвидљива вредност или вредност која се користи више пута. Ако ови услови нису испуњени, нападач може да врати кључ.

И поред ове могућности, ДСА се обично сматра сигурним ако је правилно имплементиран и користи адекватне вредности. Иако је релативно сигуран, ДСА нема тенденцију да се имплементира много у поређењу са РСА или другим методама дигиталног потписа. У поређењу са РСА, он може генерисати кључеве брже и брже је генерисати дигиталне потписе, али спорије при верификацији.

Верзија 7.0 ОпенССХ је подразумевано престала да подржава ДСА кључеве, што изгледа да је знак да се свет креће мимо ДСА-е и према другим алгоритмима.

ЕЦДСА & ЕдДСА

РСА и ДСА нису једини алгоритми за дигитални потпис, нити су најприкладнији за све ситуације. Постоји низ других, као што су ЕЦДСА и ЕдДСА, који имају својства која их чине повољним у одређеним околностима.

Нажалост, они се ослањају на још сложенију математику, као што су елиптична кривина и криптографија Едвардсове криве. Данас их нећемо детаљно покривати због ове додатне сложености, али говорићемо о неким њиховим потенцијалним позитивним и негативним стварима.

ЕЦДСА

Алгоритам дигиталног потписа Еллиптиц Цурве је варијација ДСА која укључује криптографију елиптичне криве. Пружа сличан ниво безбедности као РСА, али са много мањим кључем. То га чини ефикаснијим од РСА или ДСА у већини аспеката перформанси.

ЕдДСА

Ово је још једна ДСА алтернатива, осим што се заснива на Твистед Едвардс кривуљама. Релативно је нов што се тиче алгоритама, што има и своје предности и недостатке. Са позитивне стране, користи новије технике које повећавају његов рад.

Нажалост, новији алгоритми нису били изложени толико помно испитивању, па су многи опрезни кад одлучују да ли ће их применити или не..

Упркос томе, употреба ЕдДСА пружа висок ниво перформанси, отпорност на нападе бочних канала и уклања потребу за јединственим случајним бројем у сваком потпису. У овој фази ЕдДСА изгледа обећавајуће и почиње са ширим применама, али морат ћемо сачекати и видети да ли будуће студије проналазе рупе у безбедности.

Дигитални сертификати

Свако лако може да направи пар кључева, чак и нападач. Па, оно што спречава некога да направи гомилу кључева и прави се да је председник или да се представља као било ко други?

Па, ништа не спречава некога да тврди да је то друга особа, али постоји систем који омогућава другима да утврде да ли је особа заиста она која тврди да јесте. Зове се инфраструктура јавних кључева (ПКИ), а укључује дигитални сертификати који повезују јавни кључ појединца или ентитета са њиховим правим идентитетом. Ове потврде потписују други како би се показало колико треба да му се верује.

Процес можете упоредити са коришћењем јавних бележника за верификацију докумената. Ако неко има копију извода из матичне књиге рођених, можда ћете бити скептични у погледу тога да ли је законит закон или не. Ако је исти извод из матичне књиге рођених потписао и жигосао код јавног бележника, вероватније би било да верујете да је стварна копија.

Зашто?

Будући да потпис и печат показују да је јавни субјект од поверења видео лице и његов оригинални извод из матичне књиге рођених, тада је потврдио да је копија заиста легитимна. Јавни биљежник овјерава копију извода из матичне књиге рођених и ставља свој углед иза ње својим потписом и печатом.

Повјерење које имамо код нотара прелази се у копију извода из матичне књиге рођених, омогућавајући нам да вјерујемо далеко више од оне која није оверена.

Постоје две главне врсте сертификовања, цпотврђују ауторитете (ЦА) и мрежу поверења.

Сертификациони органи

Органи за издавање сертификата су поуздане организације које врше провјере појединаца или ентитета како би провјериле да ли су легитимни власник јавног кључа. Ако чекови открију да је појединац прави власник, ауторитет за сертификат ће потврду потписати сопственим кључем, што значи да је извршио чек и верује да су појединачни и јавни кључ легитимно повезани.

Све док верујемо ауторитету сертификата и његовом процесу верификације кључа, онда можемо веровати сертификату који је он потписао, и стога јавни кључ заиста представља ту особу.

У зависности од врсте сертификата и његове примене, различити нивои могу имати различите процесе верификације, и тако или представљају виши или нижи степен поверења.

Мрежа поверења

Мрежа поверења делује под сличном премисом, осим товде нема централних тела попут ауторитета за цертификате који обављају поступак верификације и потписују цертификате.

Уместо тога, мрежа поверења ослања се на друге појединце да потпишу потврде, стављајући своју репутацију у везу између појединца и јавног кључа. Овај систем се углавном користи са ПГП-ом, где корисници лако могу да дају сопствене сертификате.

Делује овако:

Рецимо да имате два пријатеља који желе да њихови цертификати буду потписани да доказују да су легитимни власници њихових јавних кључева. Те људе добро познајете и показују вам владине исказнице, због чега сте апсолутно сигурни да су они они за које кажу да су, и самим тим су прави власници јавних кључева за које тврде..

Будући да знате да су они легитимни власници њихових јавних кључева, радо користите свој приватни кључ за потписивање њихових потврда, улажући им вашу репутацију и у суштини кажете „Да, потврдио сам идентитет тих појединаца и они су они који тврде да јесу “. Ова два пријатеља могу вам исто учинити.

Рецимо да сваки од вашег два пријатеља има још два пријатеља који желе да им се потврде потпишу. Ако ваша два пријатеља потпишу ове друге потврде, тада можете искористити поверење које имате у своје пријатеље да прихватите да су ти други људи заиста они за које кажу да су такође.

Тада пријатељи ваших пријатеља могу да потпишу потврде људи којима верују и тако даље, на крају градећи велику мрежу појединаца у које имају поверења. Једном када ови мрежари постану довољно велики и постају повезани са другим мрежама, могу се користити као средство поверења било коме другом у мрежи.

Што више потписа на сертификату, поготово ако се ради о потписима од стране особа које имају довољно поверења, што више можете да верујете нечијем дигиталном сертификату и вези између његовог јавног кључа и његовог идентитета.

Корисници ПГП-а често одржавају кључне забаве за потписивање на којима се људи окупљају ради провјере свог идентитета и потписаних дигиталних потврда. Ова дружења помажу прикупљању нових људи у мрежи.

Иако долази са неким сложеностима, предност веб система поверења је та што не постоји централно тело које се може покварити.

Да ли су дигитални потписи безбедни?

У општем смислу, дигитални потписи су сигурни уколико приватни кључ примаоца није угрожен. Ако је власник обавестио другу особу, оставио приватни кључ записан или га је украо на други начин, нападач је могуће дигитално потписати поруке као да је власник.

То може довести до нападача који се лажно представља као жртва или вара у њиховим подацима. Ово је велики безбедносни проблем, и свако ко сумња да је њихов кључ угрожен мора опозвати свој дигитални сертификат који их повезује са њиховим јавним кључем и издати нови.

Постоји неколико других упозорења када је у питању сигурност дигиталног потписа. Треба користити одговарајући алгоритам дигиталног потписа, а такође га треба правилно имплементирати. Поред тога, такође мора постојати и начин повезивања јавног кључа са његовим власником, обично путем дигиталних сертификата.

Све док су ти захтеви испуњени, следите најбоље праксе у индустрији, а затим ваш приватни кључ није угрожен дигитални потписи су одличан начин за пружање аутентичности, интегритета и непотврђивања података.

Структурирани подаци од Каи Стацховиак под лиценцом под ЦЦ0