Что такое цифровые подписи и как они работают?

Цифровые подписи похожи на электронные версии ваших рукописных подписей. Они позволяют людям проверять подлинность и целостность данных, а также предотвращение того, чтобы подписавшая сторона могла отказаться (отрицать) свое участие.

Эти свойства привели к принятию цифровых подписей в широком спектре приложений, включая многие наши протоколы безопасности, защищенную электронную почту и управление цифровыми правами..

В этой статье мы обсудим что такое цифровые подписи, где они используются, а также технические подробности двух самых популярных алгоритмов, RSA и DSA.

Что такое цифровые подписи?

Как указано выше, цифровые подписи предоставляют нам три очень важных свойства. Это аутентификация, целостность и отсутствие отказа.

Аутентификация это процесс проверки того, что тот, кто отправляет сообщение, действительно является тем, кем они себя называют, а не самозванцем.

целостность данных или сообщения относится к тому, поступило ли оно в том же состоянии, в котором оно было отправлено. Если сообщение было изменено или подделано, оно больше не сохраняет свою целостность.

Если данные или сообщение могущий быть аннулированным, расторгнутым без, это означает, что его автор не может оспаривать, что они были истинным создателем документа. Это свойство лишает правдоподобного отрицания или старого оправдания «Извините, мой друг использовал мой аккаунт».

Пока личный ключ не был скомпрометирован, цифровые подписи могут предоставлять данные всем этим трем свойствам..

Вы можете быть удивлены, почему нам нужны эти свойства в первую очередь. Давайте сделаем шаг назад и подумаем о том, как мы делаем вещи в личной встрече.

Допустим, вы должны вашему другу Майку 100 долларов. Вы хороший человек, поэтому вы счастливы заплатить ему, когда получите деньги.

Лучший способ сделать это – просто дать Майклу счет в 100 долларов. Вы знали его годами и знаете, как он выглядит, так что это будет легко подтвердить свою личность и тем самым подтвердить, что вы отдаете деньги нужному человеку.

Если бы вы были по-настоящему анальным, вы могли бы даже проверить его удостоверение личности и заставить его подписать для вас рукописную квитанцию. Подпись на квитанции придаст ей целостность и сделает ее невосприимчивой.

Что делать, если вместо выполнения транзакции лицом к лицу вам позвонил кто-то и сказал, что это Майк, и вам следует отправить 100 долларов на номер счета 12345678?.

«Но ты не похож на Майка», – говорите вы..

“Я простудился. Отправь это сейчас, мне нужны деньги.

Вы бы отправили деньги? Возможно нет.

Нет никакого способа узнать, действительно ли это Майк или правильный номер счета. Насколько вы знаете, это может быть самозванец, который пытается украсть у вас. Вместо того, чтобы переводить деньги немедленно, лучше подождать, пока вы не увидите Майка, чтобы вы могли дать ему наличные лично..

Как и в приведенном выше сценарии, мы часто сталкиваемся с ситуациями, когда нам нужно проверить личность участника или целостность данных в онлайн-мире. Вот почему цифровые подписи выросли как механизм, который может предоставить эти свойства и облегчить безопасные онлайн-транзакции.

Без них мы можем не знать, с кем мы разговариваем, не можем быть уверены, что данные были подделаны или нет, и человек может отрицать, что они несут ответственность..

Использование цифровых подписей

Эти свойства цифровых подписей делают их полезными в самых разных приложениях. Они часто используются сами по себе или в сочетании с шифрованием в ряде различных протоколов безопасности, таких как:

• IPsec
• SSH
• TLS

Они также часто используются в управление цифровыми правами, в технология блокчейна, в управление контрактами приложения, как часть распространение программного обеспечения, И в финансы.

История цифровых подписей

Идея цифровых подписей была впервые высказана известными криптографами Уитфилдом Диффи и Мартином Хеллманом в их статье 1976 года. Новые направления в криптографии. В 1978 году Рональд Ривест, Ади Шамир и Лен Адлеман представили алгоритм RSA на всеобщее обозрение, который можно использовать для создания небезопасных цифровых подписей..

Потребовалось еще десять лет, чтобы цифровые подписи появились в широко распространенном приложении: выпуске Lotus Notes 1.0 от IBM. С тех пор цифровые подписи стали более широко применяться по мере появления новых технологий и роста потребности в онлайн-аутентификации и проверках целостности..

Краткое введение в криптографию с открытым ключом

Прежде чем мы перейдем к цифровым подписям, лучше рассмотреть некоторые важные аспекты криптографии с открытым ключом., которые составляют основу работы цифровых подписей.

Если вы относительно новичок в криптографии, система, с которой вы будете наиболее знакомы, – это шифрование с симметричным ключом. Это просто означает, что один и тот же ключ (который похож на пароль, но имеет некоторые различия) используется для шифрования и дешифрования данных.

Шифрование с открытым ключом было революцией, потому что оно включало использование отдельных ключей для процесса шифрования и дешифрования, ведущий к ряду различных криптографических приложений. Эти два ключа образовали пару ключей, состоящую из открытого ключа и личного ключа. Открытый ключ, очевидно, может быть общедоступным, в то время как закрытый ключ должен храниться в секрете, чтобы система была защищена.

Двумя наиболее распространенными видами использования криптографии с открытым ключом являются шифрование и цифровые подписи..

шифрование

Одной из новаторских особенностей криптографии с открытым ключом было то, что это позволяет сторонам, которые никогда не встречались, конфиденциально отправлять сообщения друг другу. Отправитель ищет открытый ключ нужного получателя (их можно найти на серверах открытых ключей, на персональных веб-сайтах или просто попросив человека), затем шифрует сообщение этим ключом перед отправкой получателю..

Получатель – единственный человек, который может получить доступ к сообщению – при условии, что закрытый ключ не был скомпрометирован – расшифровав его с помощью своего закрытого ключа. Несмотря на то, что открытый ключ использовался для шифрования сообщения, его можно расшифровать только с помощью закрытого ключа. Если получатель желает ответить, он находит открытый ключ исходного отправителя, а затем повторите процедуру..

Смотрите также: Общие типы шифрования объяснены

Как работают цифровые подписи?

Как мы уже говорили, цифровые подписи используются для аутентификации, чтобы увидеть, были ли данные подделаны, и для обеспечения непризнания. Существует целый ряд различных механизмов, которые можно использовать для цифровых подписей, и каждый из них имеет небольшие различия в том, как они структурированы..

В целом, эти алгоритмы должны состоять из трех подалгоритмов:

• Алгоритм генерации ключей – Этот алгоритм генерирует случайную пару ключей для пользователя. Числа, включенные в пару ключей, должны соответствовать определенным параметрам, чтобы считаться безопасными. Двумя наиболее важными аспектами являются то, что числа являются достаточно случайными и имеют адекватный размер.
• Алгоритм для подписи данных – Как только у пользователя есть свои ключи, существуют особые способы их применения к данным в процессе подписи..
• Алгоритм проверки подписи – Аналогично, проверка подписи следует заранее определенному процессу.

Чтобы система цифровой подписи была эффективной, она должна быть структурирована таким образом, чтобы:

• Данные, подписанные закрытым ключом, проверено с использованием соответствующего открытого ключа того же лица.
• Должно быть практически невозможно (с использованием современных технологий и методов) подделать действительную подпись, не зная личного ключа индивидуума.

Некоторые из наиболее распространенных схем цифровой подписи включают RSA, DSA, EcDSA и EdDSA.

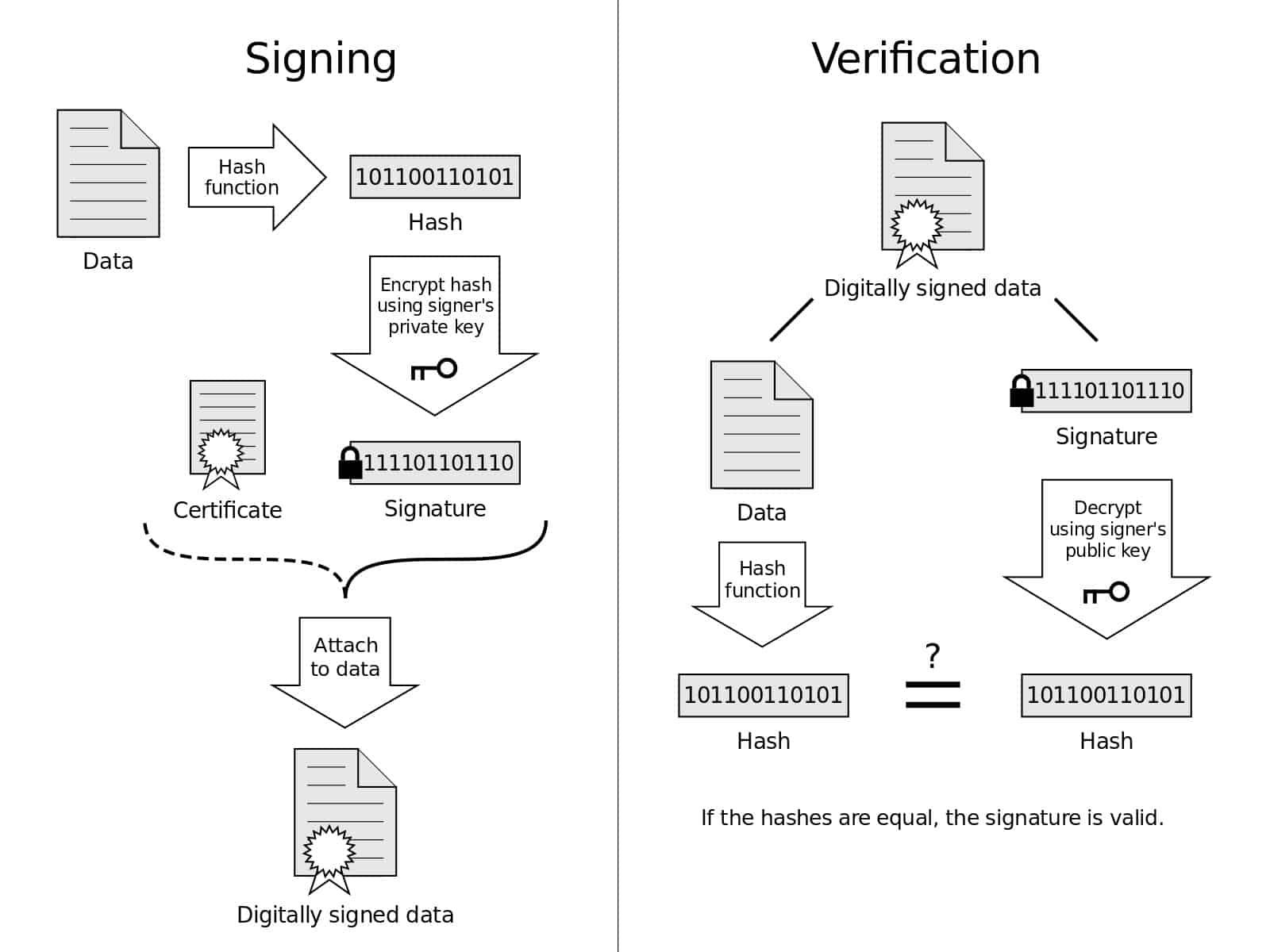
Это изображение дает визуальное представление процессов подписания и проверки. Схема цифровой подписи по лицензии Acdx под СС0

RSA

RSA был первым алгоритмом цифровой подписи, но его также можно использовать для шифрования с открытым ключом. В этой статье мы пропустим аспект шифрования, но вы можете узнать больше об этом в нашей всеобъемлющей статье, которая описывает, что такое RSA и как он работает..

Генерация ключа RSA

В безопасных реализациях RSA пары ключей обычно устанавливаются автоматически в соответствии со следующим процессом:

Премьер поколения

Выбираются два отдельных простых числа, п и Q. Точный размер этих простых чисел будет варьироваться в зависимости от размера ключа. В настоящее время для обеспечения надлежащей безопасности обычно рекомендуется использовать как минимум 2048-битные ключи RSA, поэтому мы говорим о двух простых числах, которые умножаются для получения 2048-битного числа..

2048 бит – это размер в двоичной системе счисления. Если бы число этого размера было преобразовано в нашу более знакомую десятичную систему, это было бы приблизительно так долго:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Простые числа в RSA должны выбираться случайным образом и иметь одинаковую длину.

В нашем примере мы будем использовать гораздо меньшие числа, чтобы упростить понимание. Имейте в виду, что использование ключей такого размера сделает цифровые подписи тривиальными для подделки. Вот почему такие большие значения используются на практике.

Скажем так:

п = 13

Q = 17

Первым шагом будет вычисление модуля N используя следующую формулу:

n = pq

N = 13 х 17

N = 221

Значение N также длина ключа.

Тотальная функция Кармайкла

Теперь, когда у нас есть значение для N, Следующим шагом будет использование totient-функции Кармайкла:

λ(Nзнак равно LCM (п – 1, Q – 1)

Есть несколько вещей, которые вам нужно понять:

• λ(N) означает токарт Кармайкла для значения N
• LCM представляет наименьший общий множитель. Это наименьшее общее число, которое р-1 и Q-1 можно разделить на

Давайте добавим наши цифры в уравнение:

λ(221) = LCM (13 – 1, 17 – 1)

λ(221) = LCM (12, 16)

Если вы хорошо разбираетесь в психической математике, возможно, вы поняли, что 48 самый низкий общий множитель обоих 12 и 16. Это потому, что 48 – это наименьшее число, в которое могут вписаться оба этих числа (12 x 4 = 48, 16 x 3 = 48). Следовательно:

λ(221) = 48

Подойдя с открытым ключом

В RSA открытый ключ состоит из значения N (который мы уже рассчитали как 221) и е. Поскольку открытый ключ находится в свободном доступе, значение для е не должен быть секретом. На самом деле, на практике часто устанавливается значение 65 537, поскольку большие числа замедляют процесс шифрования. В нашем примере мы установим е до 5, просто чтобы сделать его маленьким и простым числом для работы с.

Следовательно, открытый ключ для этого примера состоит из 221 и 5. Мы рассмотрим особенности применения открытого ключа в следующих разделах..

Выяснить личный ключ

Как наш открытый ключ состоит из двух чисел, так и наш закрытый ключ. Закрытые ключи состоят из d и е. Мы уже знаем значение для е (5), и мы можем использовать следующую формулу, чтобы найти d:

d = 1 /е модификация λ(N)

Обратите внимание, что модификация просто символизирует операцию по модулю, что обычно означает, что вы должны найти остаток после того, как разделите левую сторону на правую. В качестве примера:

17 мод 3 = 2

Это потому, что 3 вписывается в 17 в общей сложности 5 раз, с остатком 2.

Наш пример немного другой. «1 /е модификация”Часть уравнения может показаться, что вы делите 1 по е, но на самом деле это не так. Это сбивает с толку, но это способ представления модульная обратная. Уравнение фактически говорит нам, чтобы вычислить модульную обратную е и λ(N).

Модульное обратное обычно получается с использованием расширенного евклидова алгоритма, но мы не будем рассматривать его в этой статье. Вместо этого мы просто воспользуемся онлайн-калькулятором, чтобы упростить процесс..

Теперь, когда мы это получили, давайте введем наши значения в формулу:

d = 1/5 мод 48

Найти d, все, что нам нужно сделать, это ввести нашу ценность для е (5) в онлайн-калькулятор, где он говорит целое число, тогда наша ценность для λ(N), который 48, где это говорит по модулю.

Это дает нам результат 29 по данным онлайн калькулятора. Поэтому наш закрытый ключ будет состоять из:

е знак равно 5

d знак равно 29.

Теперь, когда мы сгенерировали оба наших ключа, следующий вопрос: «Что мы будем с ними делать?». Ну, мы могли бы использовать их для шифрования и дешифрования сообщений с помощью криптографии с открытым ключом, но эта статья о цифровых подписях, поэтому мы сосредоточимся на этом.

Цифровая подпись данных с RSA

Допустим, кто-то хочет отправить сообщение своему другу, но он хочет убедиться, что друг может проверить подлинность и целостность сообщения. Они могли бы сделать это, используя цифровую подпись RSA для подписи сообщения.

Первым шагом является запустить все сообщение через хеш-функцию. Это односторонние функции, которые всегда обеспечивают один и тот же выход для данного входа. Защищенные хеш-функции практически невозможно изменить, что означает, что выходные данные нельзя использовать для определения входных данных. Также невозможно, чтобы два отдельных сообщения имели одинаковый вывод.

Вы можете узнать больше о хэш-функциях в Что такое хеширование? Раздел нашей статьи, Шифрование, хеширование, соление – какая разница?

Допустим, мы хотим поставить цифровую подпись в сообщении «Сегодня жарко», Чтобы наш получатель мог знать, является ли сообщение подлинным или нет, и было ли оно подделано. Так что мы бы побежалиСегодня жаркоЧерез хеш-функцию.

Понимание хеш-функций

В наши дни наиболее часто используемой безопасной хэш-функцией является SHA-256. Когда мы помещаем наше сообщение через онлайн калькулятор SHA-256, оно дает нам такой результат:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Это поднимает несколько проблем для нашего примера. Во-первых, это не десятичное число, к которому привыкли большинство людей. Вы, возможно, заметили, что в этом номере есть буквы, и они доходят только до е. Это дает нам понять, что это на самом деле шестнадцатеричное число.

шестнадцатеричная система опирается на основание 16, а не основание 10, как система счисления, которую мы обычно используем. Это означает, что вместо числа, кратного 10, он считается числом, кратным 16, и первые 6 букв нашего алфавита используются для составления этих дополнительных чисел. Число, подобное этому, может быть преобразовано в нашу повседневную десятичную систему, но это выходит за рамки этой статьи..

Вторая проблема, которую мы имеем, состоит в том, что это действительно большое число. Если бы он был преобразован в десятичную, это было бы еще дольше. Поскольку мы стремимся к простоте в этом руководстве, выполнение вычислений с таким большим количеством может сделать вещи слишком запутанными, чтобы разобраться в основных понятиях..

С идеей продемонстрировать, как цифровые подписи RSA работают так, чтобы их было легко понять, мы не будем использовать такое большое значение хеш-функции в следующем примере. Вместо этого мы будем делать вид, что хэш-значение «Сегодня жаркоЭто просто 10.

Нам также придется делать вид, что, как и любой настоящий хеш, всякий раз, когда мы вводим наш вклад «Сегодня жарко» через хеш-функцию, он всегда будет возвращать значение 10. Чтобы соответствовать нормальному функционированию хэш-функций, нам нужно сделать вид, что для любого другого входного элемента невероятно малое значение. Точно так же мы должны притворяться, что также невозможно вычислить наш первоначальный вклад из этого значения. Эти свойства делают хеши очень полезными.

Как личный ключ отправителя используется для цифровой подписи хеш-значения

Наш отправитель напечатал их сообщение, а затем отправил его через хеш-функцию, которая, как мы притворяемся, вернула значение 10. После того, как отправитель получит хэш сообщения, он может создать цифровую подпись, применив свой закрытый ключ к значению хеша по следующей формуле:

м (сзнак равно сd модификация N

На самом деле это формула для расшифровки данных, которые были зашифрованы открытым ключом получателя, но она также используется для цифровой подписи документов..

Когда дело доходит до цифровых подписей:

• Значение м (с) будет подпись.
• Значение с это хеш сообщения (10).
• Значение d является частью закрытого ключа отправителя, который мы получили ранее (29).
• модификация функция та же самая операция остатка, которую мы рассмотрели ранее.
• Значение N другая часть личного ключа отправителя, которую мы рассчитали в начале (221).

Итак, давайте вложим все это в нашу формулу:

м (с) = 1029 мод 221

    м (с) = 100 000 000 000 000 000 000 000 000 000 мод 221

Давайте проведем это через следующий калькулятор по модулю (мы объяснили, как эти операции работают в Выяснение открытого ключа раздел). Для того, чтобы он работал правильно, мы должны установить наши входные данные как:

• номер тип – десятичная дробь
• номер значение – 100000000000000000000000000000
• номер б тип – десятичная дробь
• номер б значение – 221
• Вычислительное уравнение (это просто код, который сообщает калькулятору, какую операцию выполнять. Этот и другие коды можно найти на веб-странице, расположенной над разделом ввода) – мод (а, б)

Если вы все сделали правильно, это должно выглядеть так:

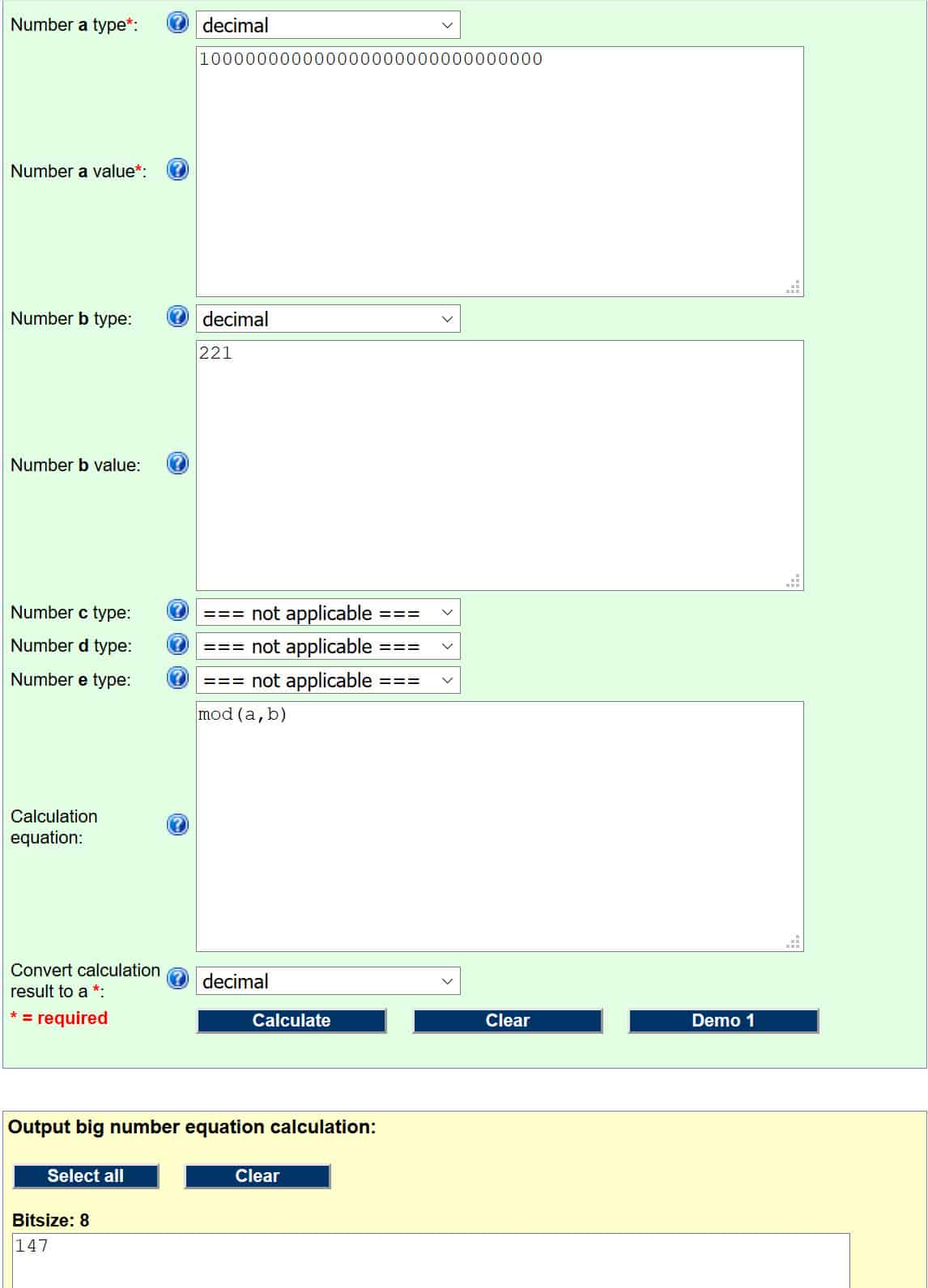
Число в желтом поле – наш ответ, поэтому цифровая подпись для хеша сообщения 147.

Чтобы доказать подлинность и целостность сообщения, наряду с предоставлением безотказности, наш отправитель должен передать сообщение «Сегодня жаркоНаряду с цифровой подписью 147 их желаемому получателю. Просто помните, что мы использовали небольшое значение для хеша, чтобы упростить вещи, вместо реального хеша сообщения.

Проверка цифровых подписей

Цифровые подписи полезны, только если мы можем проверить, являются ли они законными. Пока закрытый ключ отправителя не был скомпрометирован, получатель может проверить подлинность сообщения и его целостность, применив к цифровой подписи следующую формулу:

    см) знак равно ме модификация N

В обратном процессе подписания, это фактически формула, которая используется для шифрования данных в RSA. Когда мы используем эту формулу для проверки подписей:

• Значение см) будет хэш-значением отправителя во время его подписания (из-за структуры алгоритма открытого ключа RSA применение открытого ключа отправителя с помощью этой формулы отменит только что выполненную нами операцию подписи, в результате чего у нас останется исходный хеш-код ).
• Значение м это цифровая подпись (147).
• Значение е является частью открытого ключа отправителя, который мы получили ранее (5).
• модификация функция та же самая операция остатка, которую мы рассмотрели ранее.
• Значение N другая часть открытого ключа отправителя, которую мы рассчитали в начале (221).

Давайте бросим все это в формулу:

    см) = 1475 мод 221

    см) = 68 641 485 507 мод 221

Давайте использовать тот же калькулятор по модулю, что и раньше, и оставить все как есть, кроме:

• номер значение – 68641485507

Если вы ввели вещи правильно, вы должны получить результат:

см) = 10

Теперь, когда получатель вычислил значение хеш-функции из цифровой подписи, его следующим шагом будет вычисление значения хеш-функции полученного сообщения: «Сегодня жарко». Если вы помните из предыдущего, мы на самом деле не использовали реальный хэш сообщения SHA-256, потому что число было бы слишком большим и сделало пример слишком сложным.

Вместо этого мы притворялись, что хеш-функция фактически дает нам небольшое число, 10, для нашего вклада. Поскольку хеш-функции всегда выдают один и тот же результат для данного ввода, когда наш получатель помещает «Сегодня жарко“Через нашу мнимую хэш-функцию, они также получили бы значение 10.

Процесс проверки подписи приводит к двум значениям. Первое значение – это хеш, который был, когда отправитель подписал его цифровым ключом. Мы рассчитали это выше, используя открытый ключ отправителя..

Второе значение – это хэш сообщения, полученного получателем. Это вычисляется с использованием той же хеш-функции, которую отправитель использовал для хеширования своего исходного сообщения. Затем эти два значения сравниваются, и если значения одинаковы, то можно предположить, что сообщение является подлинным, сохраняет его целостность и что оно не подлежит исправлению. Конечно, это предполагает, что закрытый ключ отправителя не был взломан.

Поскольку наш пример вернул значение 10 для хэша, когда он был подписан отправителем, а также значение 10 как хеш сообщения, которое было получено, мы можем предположить, что сообщение «Сегодня жарко” исходит от человека, который утверждает, что отправил его, и что он не был изменен с момента его отправки.

Если получатель хочет ответить так, чтобы его корреспондент мог проверить свое сообщение таким же образом, весь процесс повторяется, за исключением того, что закрытый и открытый ключи получателя используются для процессов подписания и проверки, соответственно.

Вся эта математика, возможно, отбросила вас от самой идеи цифровых подписей. Не беспокойтесь, потому что реализации RSA автоматизируют этот процесс, так что вам не придется разбирать любые числа.

RSA профи & минусы

RSA является одним из наиболее широко поддерживаемых и реализованных алгоритмов цифровой подписи, хотя существует движение к более новым, более эффективным и безопасным алгоритмам, таким как ECDSA и EdDSA..

По сравнению с DSA (который мы рассмотрим в следующем разделе), RSA быстрее проверяет подписи, но медленнее генерирует их. Поскольку подписи обычно создаются один раз и проверяются много раз, RSA обычно предпочтительнее DSA.

DSA

Безопасность алгоритма цифровой подписи основана на двух математических концепциях, проблеме дискретного логарифма и некоторых свойствах модульного возведения в степень. Для некоторых групп невозможно вычислить их дискретные логарифмы с использованием современных методов и технологий..

Генерация ключей DSA

Для генерации ключей DSA первым шагом является выбор параметров, которые группа пользователей в одной системе может использовать для генерации пары ключей..

Генерация параметров

• Выбор хэш-функция – SHA-256 является наиболее распространенным вариантом для удовлетворения современных требований безопасности.
• Расчет на длину ключа, L и N – Эти дни, L должно быть длиной не менее 2048 бит, а N должно быть не менее 256 бит.
• Определиться с премьер, Q, это такая же длина как N.
• Выберите премьер, п, где п-1 кратно Q.
• Выберите номер, грамм, используя следующую формулу (где час произвольное число от 1 до р-1):

грамм знак равно час(п – 1) /Q модификация п

Обычно эти значения являются очень большими числами для обеспечения безопасности алгоритма. Чтобы наш пример не был слишком сложным для вычисления или объяснения, мы будем использовать гораздо меньшие числа, которые на самом деле не были бы безопасными. Скажем так:

    Q = 5

    п = 11

Найти грамм, мы вставляем наши цифры в формулу. Мы будем использовать 3 как наша ценность для час:

грамм = 3 (11-1) / 5 мод 11

грамм = 32 мод 11

грамм = 9 мод 11

Мы будем использовать тот же калькулятор по модулю, что и в Как личный ключ отправителя используется для цифровой подписи хеш-значения раздел. Параметры будут такими же, кроме:

• номер значение – 9
• номер б значение – 11

Если вы ввели все правильно, это даст вам результат для грамм из 9.

Генерация пользовательских ключей

Затем отдельные пользователи принимают эти параметры и используют их для формирования пары ключей:

• Закрытый ключ (Икс) число между 0 и Q, который мы установили на 5. Для нашего примера мы выберем 2 быть Икс, наш закрытый ключ.
• Открытый ключ (Y) рассчитывается по следующей формуле:

    Y знак равно граммИкс модификация п

Следовательно:

Y = 92 мод 11

Y = 81 мод 11

Мы будем использовать тот же калькулятор по модулю еще раз. Параметры будут такими же, кроме:

• номер значение – 81
• номер б значение – 11

Если вы ввели вещи правильно, вы должны были получить результат у = 4. Таким образом, открытый ключ 4.

Теперь, когда мы сгенерировали все наши ценности, давайте кратко подведем итоги. Параметры для системы:

• п = 11
• Q = 5
• грамм = 9

Наша ключевая пара состоит из:

• Закрытый ключ, Икс = 2
• Открытый ключ, Y = 4

Цифровая подпись данных с помощью DSA

Отправители могут использовать свой закрытый ключ DSA для цифровой подписи данных, что позволяет их получателю проверить, является ли сообщение подлинным и сохраняет ли его целостность. Это также не позволяет отправителю отказаться от сообщения..

Процесс подписи начинается с генерации случайного значения К, который между 1 и Q. Для этого примера, давайте просто выберем 3 как наше «случайное» число, К.

Затем мы следуем следующей формуле для создания индивидуального ключа (р) для сообщения:

р знак равнограммК модификация п) мод q

Давайте добавим в наши номера:

р = (93 мод 11) мод 5

р = (729 мод 11) мод 5

Мы снова используем наш калькулятор по модулю, вводя 729 и 11, что дает нам результат 3. Следовательно:

р = 3 мод 5

И затем мы повторяем операцию по модулю снова с новыми значениями, чтобы дать нам:

р = 3

Наше значение для р используется в качестве ключа для сообщения.

Мы придумали другую часть цифровой подписи, s, по следующей формуле:

s знак равно К-1(ЧАС(м) + хт) мод Q

К-1 не представляет собой принятие отрицательной силы К, но вместо того, чтобы вычислить модульное обратное, так же, как в нашем Выяснение подраздела закрытого ключа в предыдущей части статьи, где мы говорили о RSA.

ЧАС(м) – значение хеша для сообщения, которое подписывает отправитель. Обычно это будет длинное хеш-значение, полученное из сообщения, как в Понимание хеш-значений подраздел выше, который мы рассмотрели, когда мы говорили об алгоритме RSA.

В этом примере мы будем просты. Как и в разделе RSA, мы скажем, что наше сообщение, м, является “Сегодня жарко» и что хеш сообщения ЧАС(м), это 10.

Итак, давайте введем все наши значения в формулу:

s = 3-1 (10 + 2 x 3) (мод 5)

s = 3-1 (10 + 6) (мод 5)

s = 3-1 (16) (мод 5)

Теперь мы возьмем модульную обратную 3 для заказа 5 (так как 5 наша ценность для Q), используя тот же модульный обратный калькулятор из ранее. Войти 3 как целое число и 5 по модулю, который даст вам результат 2. Следовательно:

s = 2 (16) (мод 5)

s = 32 (мод 5)

Давайте вернемся к нашему калькулятору для нормальной работы по модулю, сохранив те же параметры, которые мы использовали ранее, за исключением:

• номер значение – 32
• номер б значение – 5

Если вы сделали это правильно, это даст значение для s из 2. Цифровая подпись состоит из р и s (3 и 2 соответственно). Отправители передают цифровую подпись получателю вместе со своим сообщением: «Сегодня жарко». Они также поделятся ценностями р, д, грамм и Y с их получателем.

Проверка цифровых подписей

Когда получатель получает цифровую подпись вместе с сообщением, он может проверить целостность и подлинность сообщения с помощью следующего набора вычислений..

Первый шаг – найти хеш сообщения, которое они получили. Получатель делает это, пропуская все сообщение через хеш-функцию. Для простоты и последовательности давайте скажем, что хэш сообщения, ЧАС(м) 10.

Получателю также были отправлены следующие значения, которые они используют в процессе проверки:

• Цифровая подпись (р, с) – 3, 2
• р – 1
• q – 5
• г – 9
• у – 4

Первый расчет – найти вес:

вес знак равно s-1 мод Q

Опять же, s-1 представляет взятие модульного обратного. Давайте введем наши ценности:

вес = 2-1 мод 5

Мы будем использовать модульный обратный калькулятор из ранее. Войти 2 как целое число и 5 по модулю, который даст вам результат 3 за вес. Следующий шаг – найти U1 со следующей формулой:

U1 = ЧАС(м) Икс вес модификация Q

Давайте добавим наши ценности:

U1 = 10 х 3 мод 5

U1 = 30 мод 5

Вернуться к обычному модулю калькулятора, сохранив те же параметры, которые мы использовали ранее, за исключением:

• номер значение – 30
• номер б значение – 5

Это дает нам результат 0 для U1.

Мы используем следующую формулу, чтобы придумать U2:

U2 = р Икс вес модификация Q

Давайте введем наши номера:

U2 = 3 х 3 мод 5

U2 = 9 мод 5

Затем мы возвращаемся к обычному модулю калькулятора, используя те же параметры, что и ранее, за исключением:

• номер значение – 9
• номер б значение – 5

Если вы введете это правильно, это даст вам результат для U2 из 4.

Теперь, когда у нас есть наши ценности для U1 и U2, мы можем найти v, по следующей формуле:

v = (граммu1Yu2 модификация п) мод Q

Давайте добавим в наши номера:

v = (90 х 44 мод 11) мод 5

v = (1 х 256 мод 11) мод 5

v = (256 мод 11) мод 5

Мы возвращаемся к нашему обычному модулю калькулятора, используя те же параметры, что и ранее, за исключением:

• номер значение – 256
• номер б значение – 11

Это дает нам результат 3. Следовательно:

v = 3 мод 5

Затем мы в последний раз используем обычный калькулятор по модулю, опять же с теми же параметрами, за исключением:

• номер значение – 256
• номер б значение – 11

Это дает нам результат для v из 3.

Если сообщение является подлинным и не было подделано, v будет равно r:

    v = 3

    г = 3

    3 = 3

Поэтому сообщение было отправлено владельцем закрытого ключа, и сообщение не было изменено с момента его подписания..

DSA профи & минусы

Безопасность DSA зависит от того, использует ли он адекватные номера. Кроме того р, д и грамм соблюдая правильные параметры, значение К также должен быть случайным. Это не должно быть предсказуемое значение или значение, которое используется несколько раз. Если эти требования не выполнены, злоумышленник может восстановить ключ.

Несмотря на эту возможность, DSA обычно считается безопасным, если он реализован правильно и использует адекватные значения. Несмотря на то, что DSA относительно безопасен, он, как правило, не слишком часто реализуется по сравнению с RSA или другими методами цифровой подписи. По сравнению с RSA он может генерировать ключи быстрее, а также быстрее генерировать цифровые подписи, но медленнее проверять их.

Версия 7.0 OpenSSH перестала поддерживать ключи DSA по умолчанию, что, по-видимому, является признаком того, что мир движется мимо DSA и других алгоритмов.

ECDSA & EdDSA

RSA и DSA не являются единственными алгоритмами цифровой подписи и не являются наиболее подходящими для всех ситуаций. Есть ряд других, таких как ECDSA и EdDSA, которые имеют свойства, которые делают их предпочтительными в определенных обстоятельствах.

К сожалению, они основаны на еще более сложной математике, такой как эллиптическая кривая и криптография Эдвардса. Мы не будем подробно освещать их сегодня из-за этой дополнительной сложности, но мы поговорим о некоторых их потенциальных плюсах и минусах..

ECDSA

Алгоритм цифровой подписи эллиптической кривой представляет собой разновидность DSA, которая включает в себя криптографию с эллиптической кривой. Он обеспечивает уровень безопасности, аналогичный RSA, но с гораздо меньшим ключом. Это делает его более эффективным, чем RSA или DSA, в большинстве аспектов производительности..

EdDSA

Это еще одна альтернатива DSA, за исключением того, что она основана на кривых Twisted Edwards. Это относительно новый алгоритм, который имеет свои преимущества и недостатки. С положительной стороны, он использует новые методы, которые повышают его производительность.

К сожалению, более новые алгоритмы не подвергались такому тщательному анализу, поэтому многие люди осторожны, решая, применять их или нет..

Несмотря на это, использование EdDSA обеспечивает высокий уровень производительности, устойчивость к атакам по побочным каналам и устраняет необходимость в уникальном случайном числе в каждой подписи. На данном этапе EdDSA выглядит многообещающе и начинает видеть более широкую реализацию, но нам придется подождать и посмотреть, найдут ли будущие исследования какие-либо дыры в безопасности.

Цифровые сертификаты

Любой может легко составить пару ключей, даже атакующий. Так что же мешает кому-то сделать кучу ключей и притвориться, что они президент, или выдать себя за кого-то другого??

Что ж, ничто не мешает кому-то утверждать, что он является другим человеком, но существует система, которая позволяет другим выяснить, действительно ли человек является тем, кем он себя считает. Это называется инфраструктура открытых ключей (PKI), и это включает в себя цифровые сертификаты, которые связывают открытый ключ физического или юридического лица с их подлинной личностью. Эти сертификаты подписаны другими, чтобы указать, насколько сертификат должен доверять.

Вы можете сравнить процесс с использованием нотариусов для проверки документов. Если у кого-то есть копия свидетельства о рождении, вы можете скептически относиться к тому, является ли оно законным. Если это же свидетельство о рождении было подписано и заверено печатью нотариуса, вы, скорее всего, поверите, что это настоящая копия.

Почему?

Поскольку подпись и печать показывают, что доверенный публичный субъект видел человека и его оригинальное свидетельство о рождении, то подтвердил, что копия на самом деле является законной. Нотариус заверяет копию свидетельства о рождении и ставит свою репутацию за подписью и печатью.

Доверие, которое мы имеем к нотариусу, передается в копию свидетельства о рождении, что позволяет нам доверять ему гораздо больше, чем то, которое не было заверено нотариально..

Существует два основных типа сертификации:центры сертификации (CA) и сеть доверия.

Центры сертификации

Центры сертификации доверенные организации, которые проводят проверки физических или юридических лиц, чтобы проверить, являются ли они законным владельцем открытого ключа. Если проверки показывают, что лицо является истинным владельцем, то центр сертификации подпишет сертификат своим собственным ключом, что означает, что он завершил проверку и считает, что индивидуальный и открытый ключи законно связаны.

Пока мы доверяем центру сертификации и его процессу проверки ключа, мы можем доверять сертификату, подписанному ими., и, таким образом, что открытый ключ действительно представляет этого человека.

В зависимости от типа сертификата и его применения, разные уровни могут иметь разные процессы проверки, и, таким образом, либо представляют собой более высокую или более низкую степень доверия.

Сеть доверия

Сеть доверия работает в аналогичной предпосылке, за исключениемздесь нет центральных органов как центры сертификации, которые выполняют процесс проверки и подписывают сертификаты.

Вместо этого сеть доверия полагается на то, что другие люди подписывают сертификаты, размещая свою репутацию на связи между этим лицом и открытым ключом. Эта система в основном используется с PGP, где пользователи могут легко создавать свои собственные сертификаты.

Это работает так:

Допустим, у вас есть два друга, которые хотят, чтобы их сертификаты были подписаны, чтобы доказать, что они являются законными владельцами своих открытых ключей. Вы хорошо знаете этих людей, и они показывают вам свои правительственные удостоверения личности, что дает вам абсолютную уверенность в том, что они являются теми, кем себя называют, и, таким образом, являются настоящими владельцами открытых ключей, на которые они претендуют..

Поскольку вы знаете, что они являются законными владельцами своих открытых ключей, вы с радостью используете свой закрытый ключ для подписи своих сертификатов, ставя свою репутацию на них и по сути говоря: «Да, я проверил личности этих людей, и они являются теми, кто они утверждают, что были ». Эти два друга могут сделать то же самое с вами.

Допустим, у каждого из ваших двух друзей есть еще два друга, которые хотят подписать свои сертификаты. Если ваши два друга подписывают эти другие сертификаты, то вы можете использовать доверие своих друзей, чтобы признать, что эти другие люди действительно те, кем они себя называют..

Друзья ваших друзей могут затем подписать сертификаты людей, которым они доверяют, и так далее, в конечном итоге создав большую сеть людей, которым доверяют. Как только эти сети становятся достаточно большими и становятся взаимосвязанными с другими сетями, их можно использовать как средство доверия кому-либо еще в сети.

Чем больше подписей на сертификате, особенно если это подписи от доверенных лиц, тем больше вы можете доверять чьему-то цифровому сертификату и связи между его открытым ключом и его личностью.

Пользователи PGP часто проводят вечеринки подписи ключей, где люди собираются, чтобы проверить свою личность и подписать свои цифровые сертификаты. Эти собрания помогают привлечь новых людей в сеть.

Хотя это связано с некоторыми сложностями, преимущество системы доверия состоит в том, что нет центрального органа, который может быть поврежден.

Безопасны ли цифровые подписи??

В общем смысле, цифровые подписи являются безопасными, если закрытый ключ получателя не был взломан. Если владелец сообщил другому лицу, оставил записанный закрытый ключ или украл его другим способом, то злоумышленник может подписать сообщения цифровой подписью, как если бы они были владельцем.

Это может привести к тому, что злоумышленник будет выдавать себя за жертву или подделывать ее данные. Это огромная проблема безопасности, и любой, кто подозревает, что их ключ был скомпрометирован, должен отозвать свой цифровой сертификат, который связывает их с открытым ключом, и выдать новый..

Есть несколько других предостережений, когда речь идет о безопасности цифровых подписей. Следует использовать соответствующий алгоритм цифровой подписи, и его также необходимо правильно реализовать. Наряду с этим, также должен быть способ связать открытый ключ с его владельцем, обычно через цифровые сертификаты..

Пока эти требования соблюдены, вы следуете передовым отраслевым практикам, и ваш закрытый ключ не был скомпрометирован, тогда Цифровые подписи являются отличным способом обеспечить подлинность, целостность и неприкосновенность данных.

Структурированные данные Кай Стаховяк, лицензированный под СС0