Что такое шифрование RSA и как оно работает?

Шифрование RSA – это система, которая решает то, что когда-то было одной из самых больших проблем в криптографии: Как вы можете отправить кому-то закодированное сообщение не имея возможности ранее поделиться кодом с ними?

Эта статья научит вас всему, что вам нужно знать о как было разработано шифрование RSA, как это устроено, математика за этим, для чего он используется а также некоторые из самые большие проблемы безопасности, с которыми он сталкивается. Изучение RSA даст вам некоторые базовые знания, которые помогут вам понять, сколько частей нашей онлайн-жизни защищены.

Что такое шифрование RSA?

Допустим, вы хотите рассказать своему другу секрет. Если вы рядом с ними, вы можете просто прошептать это. Если вы находитесь на противоположных сторонах страны, это явно не сработает. Вы можете записать это и отправить по почте им или использовать телефон, но каждый из этих каналов связи небезопасен и любой с достаточно сильной мотивацией может легко перехватить сообщение.

Если бы секрет был достаточно важен, вы не рискнули бы его записать в обычном порядке – шпионы или мошенник-почтальон могли бы просмотреть вашу почту. Кроме того, кто-то может прослушивать ваш телефон без вашего ведома и регистрировать каждый ваш звонок.

Одним из способов предотвращения доступа перехватчиков к содержимому сообщения является зашифровать его. Это в основном означает добавление кода к сообщению, которое превращает его в беспорядочный беспорядок. Если ваш код достаточно сложен, то единственные люди, которые смогут получить доступ к исходному сообщению, это те, кто имеет доступ к коду.

Если у вас была возможность поделиться кодом с вашим другом заранее, то любой из вас может отправить зашифрованное сообщение в любое время, зная, что вы двое – единственные, у кого есть возможность прочитать содержимое сообщения. Но что, если у вас не было возможности поделиться кодом заранее?

Это одна из фундаментальных проблем криптографии, которая решается схемы шифрования с открытым ключом (также известные как асимметричное шифрование), такие как RSA.

При шифровании RSA сообщения шифруются с помощью кода, называемого открытый ключ, которыми можно поделиться открыто. Из-за некоторых четких математических свойств алгоритма RSA, если сообщение было зашифровано открытым ключом, оно может быть расшифровано только другим ключом, известным как закрытый ключ. У каждого пользователя RSA есть пара ключей, состоящая из их открытого и закрытого ключей. Как следует из названия, закрытый ключ должен храниться в секрете.

Схемы шифрования с открытым ключом отличаются от шифрование с симметричным ключом, где и в процессе шифрования, и в дешифровании используется один и тот же закрытый ключ. Эти различия делают шифрование с открытым ключом, такое как RSA, полезным для связи в ситуациях, когда не было возможности безопасно распространять ключи заранее..

Алгоритмы с симметричным ключом имеют свои собственные приложения, такие как шифрование данных для личного использования или для случаев, когда существуют защищенные каналы, по которым закрытые ключи могут совместно использоваться..

Смотрите также: Криптография с открытым ключом

Где используется шифрование RSA?

RSA-шифрование часто используется в комбинация с другими схемами шифрования, или для цифровые подписи который может доказать подлинность и целостность сообщения. Обычно он не используется для шифрования целых сообщений или файлов, потому что он менее эффективен и требует больше ресурсов, чем шифрование с симметричным ключом..

Чтобы сделать вещи более эффективными, файл обычно шифруется с помощью алгоритма симметричного ключа, а затем симметричный ключ шифруется с помощью шифрования RSA.. В рамках этого процесса только объект, имеющий доступ к закрытому ключу RSA, сможет расшифровать симметричный ключ..

Не имея доступа к симметричному ключу, исходный файл не может быть расшифрован. Этот метод можно использовать для обеспечения безопасности сообщений и файлов, не занимая слишком много времени и не занимая слишком много вычислительных ресурсов..

Шифрование RSA может использоваться в ряде различных систем. Это может быть реализовано в OpenSSL, wolfCrypt, cryptlib и ряде других криптографических библиотек..

Являясь одной из первых широко используемых схем шифрования с открытым ключом, RSA заложила основы для большей части наших безопасных коммуникаций. это было традиционно используется в TLS и был также оригинальный алгоритм, используемый в шифровании PGP. RSA по-прежнему используется в различных веб-браузерах, электронной почте, VPN, чатах и ​​других каналах связи..

RSA также часто используется для создания безопасных соединений между VPN-клиентами и VPN-серверами. В таких протоколах, как OpenVPN, рукопожатия TLS могут использовать алгоритм RSA для обмена ключами и установления безопасного канала..

Фон шифрования RSA

Как мы упоминали в начале этой статьи, до шифрования с открытым ключом было сложно обеспечить безопасную связь, если не было возможности безопасно обменяться ключами заранее. Если бы не было возможности поделиться кодом заранее или создать безопасный канал, по которому можно было бы распространять ключи, не было бы возможности общаться без угрозы, что враги смогут перехватить и получить доступ к содержимому сообщения..

Лишь в 1970-х годах ситуация начала меняться. Первое крупное развитие в направлении того, что мы сейчас называем криптографией с открытым ключом, было опубликовано в начале десятилетия Джеймсом Эллисом. Эллис не мог найти способ реализовать свою работу, но его коллега Клиффорд Кокс расширил его, чтобы стать тем, что мы теперь знаем как RSA-шифрование.

Последняя часть головоломки – это то, что мы сейчас называем Обмен ключами Диффи-Хеллмана. Малколм Дж. Уильямсон, другой сотрудник, выяснил схему, которая позволяла двум сторонам совместно использовать ключ шифрования, даже если злоумышленники контролировали канал.

Вся эта работа была предпринята в разведывательном агентстве Великобритании, правительственном штабе связи (GCHQ), который держал открытие в секрете. Частично из-за технологических ограничений GCHQ не мог видеть использование криптографии с открытым ключом в то время, поэтому разработка стояла на полке, пылясь. Лишь в 1997 году работа была рассекречена, и первоначальные изобретатели RSA были признаны.

Спустя несколько лет подобные концепции начали развиваться в публичной сфере. Ральф Меркл создал раннюю форму криптография с открытым ключом, который повлиял на Уитфилда Диффи и Мартина Хеллмана в дизайне обмена ключами Диффи-Хеллмана.

В идеях Диффи и Хеллмана отсутствовал один важный аспект, который сделал бы их работу основой криптографии с открытым ключом. Это был односторонняя функция, которую было бы трудно инвертировать. В 1977 году, Рон Ривест, Ади Шамир и Леонард Адлеман, чьи фамилии образуют аббревиатуру RSA, после года работы над решением этой проблемы было найдено решение.

Ученые из Массачусетского технологического института совершили прорыв после Пасхальной вечеринки в 1977 году. После ночи питья Ривест отправился домой, но вместо сна он лихорадочно провел вечер, сочиняя статью, в которой его идея была оформлена для необходимой односторонней функции..

Идея была запатентована в 1983 году MIT, но только в первые дни Интернета, алгоритм RSA начал рассматривать широкое распространение как важный инструмент безопасности.

Как работает шифрование RSA?

Следующее будет немного упрощением, потому что слишком много читателей, вероятно, получили шрамы от своего учителя математики в средней школе. Чтобы математика не вышла из-под контроля, мы будем упрощение некоторых концепций и использование гораздо меньших чисел. В действительности, шифрование RSA использует простые числа, которые намного больше по величине, и есть несколько других сложностей.

Есть несколько различных концепций, которые вы должны обдумать, прежде чем мы сможем объяснить, как все это сочетается. Это включает функции люка, порождающие простые числа, общая функция Кармайкла и отдельные процессы, участвующие в вычисление открытых и закрытых ключей используется в процессах шифрования и дешифрования.

Функции люка

RSA-шифрование работает при условии, что алгоритм легко вычислить в одном направлении, но почти невозможно наоборот. Например, если вам сказали, что 701111 – это произведение двух простых чисел, вы бы смогли выяснить, что это за два числа?

Даже с калькулятором или компьютером, большинство из нас не будет знать, с чего начать, не говоря уже о том, чтобы найти ответ. Но если мы перевернем вещи, это станет намного проще. Каков результат:

907 х 773

Если бы вам было достаточно скучно, вы бы смогли вытащить свой телефон или, возможно, посчитать его в своей голове, чтобы обнаружить, что ответ – это ранее упомянутые 701111. Эти 907 и 773 являются простыми числами, которые отвечают на наш первый вопрос, который показывает нам, что некоторые уравнения можно легко вычислить одним способом, но, по-видимому, невозможно наоборот.

Еще один интересный аспект этого уравнения заключается в том, что легко вычислить одно из простых чисел, если у вас уже есть другое, а также продукт. Если вам говорят, что 701111 является результатом 907, умноженного на другое простое число, вы можете выяснить это другое простое число с помощью следующего уравнения:

701,111 ÷ 907 = 773

Поскольку связь между этими числами проста для вычисления в одном направлении, но невероятно сложна в обратном, уравнение известно как функция люка. Имейте в виду, что, хотя вышеприведенный пример трудно понять людям, компьютеры могут выполнить операцию за тривиальное время.

Из-за этого RSA использует гораздо большие числа. Размер простых чисел в реальной реализации RSA варьируется, но в 2048-битном RSA они собираются вместе для создания ключей длиной 617 цифр. Чтобы помочь вам визуализировать это, ключом будет число такого размера:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

Генерация простых чисел

Упомянутые выше функции «ловушки» образуют основу для работы схем шифрования с открытым и закрытым ключами.. Их свойства позволяют открывать открытые ключи, не подвергая опасности сообщение и не раскрывая закрытый ключ.. Они также позволяют шифровать данные одним ключом таким способом, который может быть расшифрован только другим ключом из пары..

Первым шагом шифрования сообщения с помощью RSA является генерировать ключи. Для этого нам нужно два простых числа (п и Q) которые выбраны с тестом на первичность. Тест на простоту – это алгоритм, который эффективно находит простые числа, такой как тест на простоту Рабина-Миллера.

Простые числа в RSA должны быть очень большими, а также относительно далеко друг от друга. Числа, которые являются маленькими или ближе друг к другу, намного легче взломать. Несмотря на это, в нашем примере будут использоваться меньшие числа, чтобы было легче следить и вычислять.

Допустим, тест на простоту дает нам простые числа, которые мы использовали выше, 907 и 773. Следующим шагом является обнаружение модуля (N), используя следующую формулу:

N знак равно п Икс Q

где п = 907 и Q = 773

Следовательно:

N = 907 х 773

N = 701,111

Тотальная функция Кармайкла

Как только мы N, мы используем Общая функция Кармайкла:

    λ(Nзнак равно LCM (п – 1, Q – 1)

Если прошло некоторое время с тех пор, как вы прочитали учебники по математике, вышеприведенное может показаться немного пугающим. Вы можете пропустить эту часть и просто поверить, что математика работает, в противном случае оставайтесь с нами для нескольких дополнительных вычислений. Все будет объяснено как можно более подробно, чтобы помочь вам разобраться в основах.

Для тех, кто не в курсе, λ (п) представляет кармайкл N, пока LCM означает самый низкий общий множитель, который является самым низким числом, которое оба п и Q можно разделить на. Есть несколько различных способов выяснить это, но самый простой – довериться онлайн-калькулятору, который сделает уравнение для вас. Итак, давайте поместим наши числа в уравнение:

    λ(701111знак равно LCM (907 – 1, +773 – 1)

    λ(701111знак равно LCM (906, +772)

   Используя калькулятор, связанный выше, это дает нам:

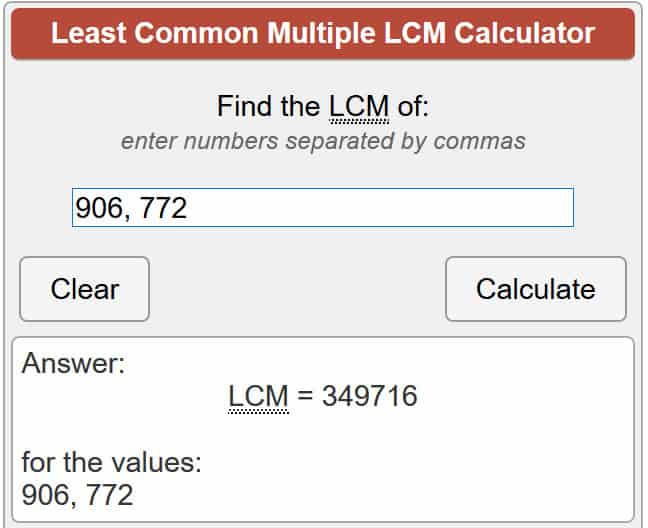
    λ(701111) = 349 716

Генерация открытого ключа

Теперь, когда у нас есть число Кармайкла наших простых чисел, это время, чтобы выяснить наш открытый ключ. Под RSA, открытые ключи состоят из простого числа е, также как и N. Число е может быть что угодно между 1 и значением для λ(N), что в нашем примере составляет 349,716.

Поскольку открытый ключ передается открыто, это не так важно для е быть случайным числом. На практике, е обычно устанавливается на 65537, потому что, когда случайным образом выбираются гораздо большие числа, шифрование становится намного менее эффективным. Для сегодняшнего примера, мы будем делать небольшие цифры, чтобы сделать вычисления эффективными. Давайте скажем:

е = 11

Наши последние зашифрованные данные называются зашифрованным текстом (с). Мы выводим это из нашего открытого текста сообщения (м), применяя открытый ключ по следующей формуле:

с знак равно ме мод n

Мы уже придумали е и мы знаем N также. Единственное, что нам нужно объяснить, это модификация. Это немного из глубины этой статьи, но это относится к по модулю операции, что по существу означает остаток, оставшийся, когда вы делите одну сторону на другую. Например:

10 модификация 3 = 1

Это потому, что 3 входит в 10 три раза с остатком 1.

Вернемся к нашему уравнению. Для простоты, давайте скажем, что сообщение (м) что мы хотим зашифровать и сохранить в тайне это просто одно число, 4. Давайте подключим все:

с знак равно ме модификация N

с = 411 модификация 701111

с = 4 194 304 модификация 701111

Опять же, чтобы сделать по модулю операции Легко, мы будем использовать онлайн калькулятор, но вы можете сами в этом разобраться. Ввод 4 194 304 в онлайн-калькулятор, он дает нам:

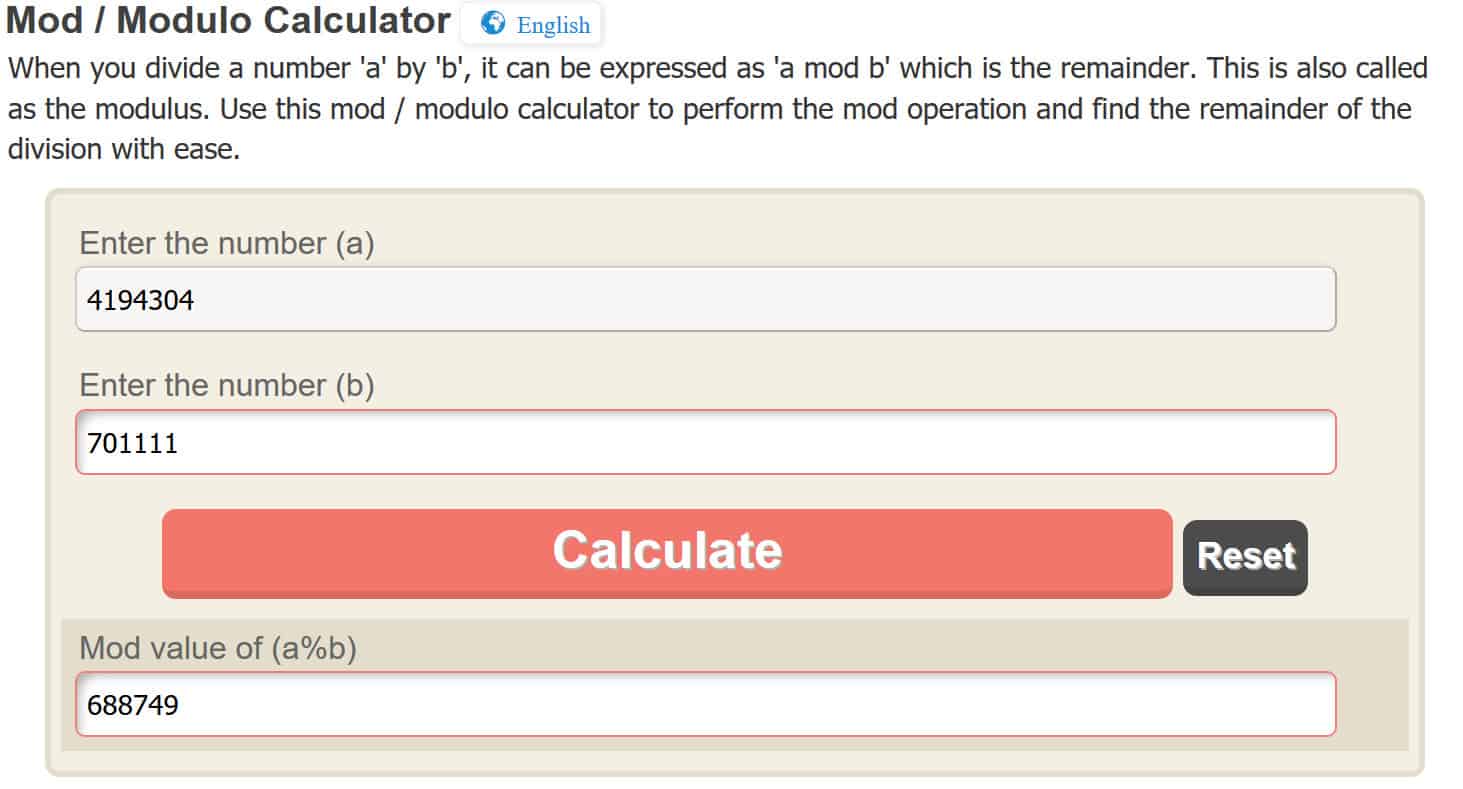
с = 688 749

Поэтому, когда мы используем RSA для шифрования нашего сообщения, 4, с нашим открытым ключом, это дает нам зашифрованный текст 688,749. Предыдущие шаги могли показаться слишком сложными, но важно повторить то, что на самом деле произошло.

У нас был сообщение 4, который мы хотели сохранить в секрете. Мы применили к нему открытый ключ, который дал нам зашифрованный результат 688 749. Теперь, когда он зашифрован, мы можем безопасно отправить номер 688,749 владельцу пары ключей. Они являются единственным человеком, который сможет расшифровать его с помощью своего закрытого ключа. Когда они расшифруют его, они увидят сообщение, которое мы действительно отправляли., 4.

Генерация закрытого ключа

В RSA-шифровании после преобразования данных или сообщений в зашифрованный текст с открытым ключом их можно расшифровать только с помощью закрытого ключа из той же пары ключей.. Закрытые ключи состоят из d и N. Мы уже знаем N, и следующее уравнение используется, чтобы найти d:

d = 1 /е мод λ(N)

в Генерация открытого ключа раздел выше, мы уже решили, что в нашем примере, е будет равно 11. Точно так же мы знаем, что λ(N) равняется 349 716 от нашей предыдущей работы под Тотальная функция Кармайкла. Все становится немного сложнее, когда мы сталкиваемся с этим разделом формулы:

1 /е модификация

Это уравнение может выглядеть так, будто оно просит вас разделить 1 на 11, но это не так. Вместо этого это просто символизирует, что нам нужно рассчитать модульная обратная из е (который в данном случае равен 11) и λ(N) (что в данном случае составляет 349 716).

По сути это означает, что вместо выполнения стандартной операции по модулю, мы будем использовать вместо. Обычно это встречается в расширенном евклидовом алгоритме, но это немного выходит за рамки этой статьи, поэтому мы будем просто обманывать и использовать вместо этого онлайн-калькулятор. Теперь, когда мы понимаем все, что происходит, давайте включим нашу информацию в формулу:

d = 1 /11 модификация 349716

Чтобы выполнить эту операцию, просто введите 11 (или любое значение, которое вы можете иметь для е если вы пытаетесь это на собственном примере), где это говорит целое число и 349 716 (или любое значение, которое вы можете иметь для λ(N) если вы пытаетесь это на собственном примере), где говорится Модульное в онлайн калькуляторе, который был связан выше. Если вы сделали это правильно, вы должны получить результат, где:

d = 254, 339

Теперь, когда у нас есть значение для d, мы можем расшифровать сообщения, которые были зашифрованы с помощью нашего открытого ключа, используя следующую формулу:

м знак равно сd мод n

Теперь мы можем вернуться к зашифрованному тексту, который мы зашифровали под Генерация закрытого ключа раздел. Когда мы зашифровали сообщение открытым ключом, это дало нам значение для с 688 749. Сверху мы знаем, что d равняется 254 339. Мы также знаем, что N равно 701111. Это дает нам:

м = 688 749254339 модификация 701111.

Как вы, возможно, заметили, попытка привести число к 254 339-й степени может быть немного больше для большинства обычных калькуляторов. Вместо этого мы будем использовать онлайн-калькулятор расшифровки RSA. Если вы хотите использовать другой метод, вы бы применили полномочия, как обычно, и выполняли бы операцию модуля так же, как мы это делали в Генерация открытого ключа раздел.

В калькуляторе, указанном выше, введите 701111, где написано Модуль питания: N, 254,399, где говорится Ключ расшифровки: D, и 688 749, где говорится Зашифрованное сообщение в числовой форме, как показано ниже:

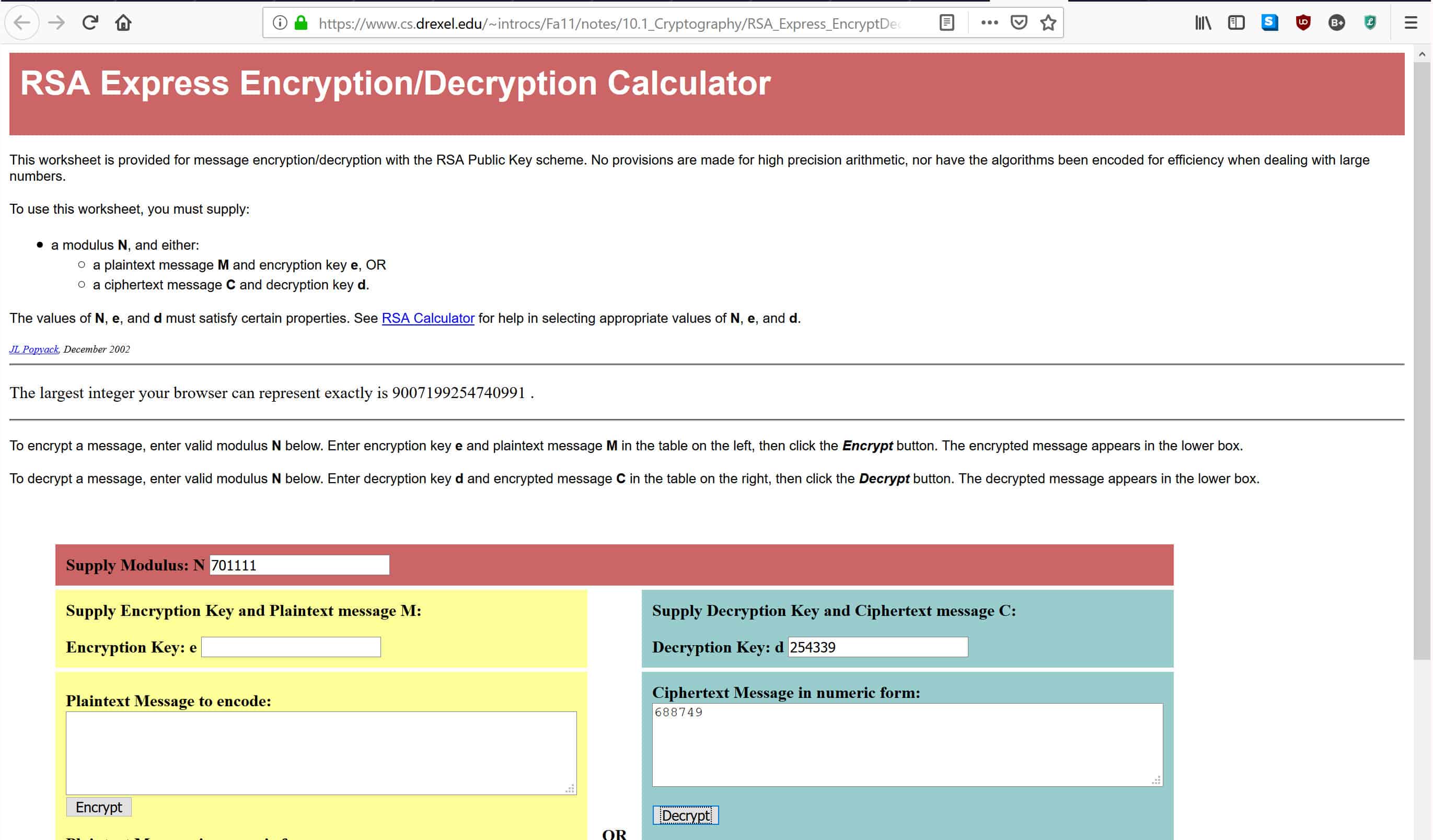
После ввода данных нажмите Расшифровать, который поместит числа через формулу расшифровки, которая была перечислена выше. Это даст вам оригинальное сообщение в поле ниже. Если вы все сделали правильно, вы должны получить ответ 4, который был исходным сообщением, которое мы зашифровали с нашим открытым ключом.

Как работает шифрование RSA на практике

Приведенные выше разделы должны дать вам разумное представление о том, как работает математика шифрования с открытым ключом. Это может немного сбивать с толку, но даже те, кто не разбирается в тонкостях уравнений, могут надеяться забрать некоторую важную информацию о процессе.

На шагах, перечисленных выше, мы показали, как два объекта могут безопасно общаться без предварительного совместного использования кода. Во-первых, каждый из них должен создать свои собственные пары ключей и поделиться открытым ключом друг с другом. Эти два объекта должны держать свои секретные ключи в секрете, чтобы их связь оставалась безопасной.

Когда у отправителя есть открытый ключ получателя, он может использовать его для шифрования данных, которые он хочет сохранить в безопасности.. Как только он был зашифрован с открытым ключом, он может быть расшифрован только с помощью закрытого ключа из той же пары ключей. Даже один и тот же открытый ключ не может быть использован для расшифровки данных. Это связано со свойствами функции люка что мы упоминали выше.

Когда получатель получает зашифрованное сообщение, он использует свой закрытый ключ для доступа к данным. Если получатель хочет вернуть связь безопасным способом, затем они могут зашифровать свое сообщение открытым ключом стороны, с которой они общаются. Опять же, после того, как он был зашифрован с открытым ключом, единственный доступ к информации – через соответствующий закрытый ключ..

Таким образом, шифрование RSA может использоваться ранее неизвестными сторонами для безопасной передачи данных между собой. Значительные части каналов связи, которые мы используем в нашей онлайн-жизни, были созданы из этого фонда.

Как более сложные сообщения шифруются с помощью RSA?

В нашем примере мы сильно упростили вещи, чтобы их было легче понять, поэтому мы зашифровали только сообщение «4». Возможность шифрования числа 4 не кажется особенно полезной, так что вы можете удивиться как вы можете зашифровать более сложный набор данных, такой как симметричный ключ (который является наиболее распространенным использованием RSA), или даже сообщение.

Некоторые люди могут быть озадачены тем, как ключ типа «n38cb29fkbjh138g7fqijnf3kaj84f8b9f…» или сообщение типа «купи мне сэндвич» можно зашифровать с помощью алгоритма, такого как RSA, который работает с числами, а не буквами. Реальность такова, что вся информация, которую обрабатывают наши компьютеры, хранится в двоичном формате (1 и 0), и мы используем такие стандарты кодирования, как ASCII или Unicode представлять их так, чтобы люди могли их понять (буквы).

Это означает, что ключи типа «n38cb29fkbjh138g7fqijnf3kaj84f8b9f…» и сообщения типа «купи мне сэндвич» уже существуют в виде чисел, который может быть легко вычислен в алгоритме RSA. Числа, которыми они представлены, намного больше и сложнее для нас, поэтому мы предпочитаем иметь дело с буквенно-цифровыми символами, а не с беспорядочными двоичными числами..

Если бы вы хотели зашифруйте более длинный сеансовый ключ или более сложное сообщение с помощью RSA, для этого потребуется гораздо большее число.

набивка

Когда RSA реализован, он использует то, что называется прокладка, чтобы помочь предотвратить ряд атак. Чтобы объяснить, как это работает, мы начнем с примера. Допустим, вы отправляли закодированное сообщение другу:

Дорогая Карен,

    Я надеюсь, что с тобой все в порядке. Мы еще обедаем завтра?

    Искренне Ваш,

    Джеймс

Допустим, вы закодировали сообщение простым способом: меняя каждую букву на ту, которая следует за ней в алфавите. Это изменит сообщение на:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm. Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

Если ваши враги перехватили это письмо, есть хитрость, которую они могут использовать, чтобы попытаться взломать код. Они могли посмотрите на формат вашего письма и попытайтесь угадать, что может быть сказано в сообщении. Они знают, что люди обычно начинают свои письма с «Привет», «Привет», «Дорогой» или ряда других соглашений..

Если они попытаются применить «Привет» или «Привет» в качестве первого слова, они увидят, что оно не будет соответствовать количеству символов. Затем они могут попробовать «Дорогой». Это подходит, но это не обязательно что-то значит. Злоумышленники просто попробуют и увидят, куда они их привели. Таким образом, они будут менять буквы «е», «f», «b» и «s» на «d», «e», «a» и «r» соответственно. Это дало бы им:

Уважаемый Ласео,

    J ipqe zpv являются xemm. Являются ли xe tujmm iawjoh djooes upnpsspx?

    Зпврт тьодеремз,

    Kanet

Это все еще выглядит довольно запутанно, поэтому злоумышленники могут попытаться взглянуть на некоторые другие соглашения, например, как мы заканчиваем наши письма. Люди часто добавляют «От» или «С наилучшими пожеланиями» в конце, но ни один из них не соответствует формату. Вместо этого злоумышленники могут попробовать «Искренне ваш» и заменить другие буквы, чтобы увидеть, где он их получает. Путем замены «z», «p», «v», «t», «j», «o», «d» и «m» на «y», «o», «u», «s», « i »,« n »,« c »и« l »соответственно, они получат:

Уважаемый Лазен,

    Я думаю, ты xell. Есть ли у меня дела??

    Искренне Ваш,

    Kanet

После этой модификации похоже, что злоумышленники начинают куда-то добираться. Они нашли слова «я», «ты» и «есть», в дополнение к словам, которые составляли их первоначальные догадки.

Видя, как слова расположены в правильном грамматическом порядке, злоумышленники могут быть уверены, что они движутся в правильном направлении. К настоящему времени они, вероятно, также поняли, что код включает в себя замену каждой буквы на букву, следующую за ней в алфавите.. Как только они осознают это, это позволяет легко перевести остальное и прочитать оригинальное сообщение..

Приведенный выше пример был простым кодом, но, как вы можете видеть,, структура сообщения может дать злоумышленникам подсказки о его содержании. Конечно, было трудно понять сообщение только из его структуры, и потребовались некоторые образованные догадки, но вы должны помнить, что компьютеры гораздо лучше справляются с этим, чем мы.. Это означает, что они могут быть использованы для определения более сложных кодов за гораздо более короткое время, основанный на подсказках, которые прибывают из структуры и других элементов.

Если структура может привести к взлому кода и раскрытию содержимого сообщения, то нам нужен какой-то способ скрыть структуру, чтобы обеспечить безопасность сообщения. Это подводит нас к набивка.

Когда сообщение дополняется, добавлены рандомизированные данные, чтобы скрыть исходные ключи форматирования, которые могут привести к повреждению зашифрованного сообщения. С RSA все немного сложнее, потому что зашифрованный ключ не имеет очевидного форматирования письма, что помогло нам понять в нашем примере выше.

Несмотря на это, злоумышленники могут использовать ряд атак для использования математических свойств кода и взлома зашифрованных данных. Из-за этой угрозы, реализации RSA используют схемы заполнения, такие как OAEP, для встраивания дополнительных данных в сообщение. Добавление этого отступа перед шифрованием сообщения делает RSA намного более безопасным.

Подписание сообщений

RSA может использоваться не только для шифрования данных. Его свойства также делают его полезной системой для подтверждение того, что сообщение было отправлено объектом, который утверждает, что отправило его, а также доказательство того, что сообщение не было изменено или подделано.

Когда кто-то хочет доказать подлинность своего сообщения, он может вычислить гашиш (функция, которая берет данные произвольного размера и превращает их в значение фиксированной длины) открытого текста, а затем подписывает их своим закрытым ключом. Oни подписать хеш, применяя ту же формулу, которая используется при расшифровке (м = сd мод n). Как только сообщение подписано, они отправляют эту цифровую подпись получателю вместе с сообщением.

Если получатель получает сообщение с цифровой подписью, он может использовать подпись для проверки подлинности подписи сообщения личным ключом лица, которое утверждает, что оно отправлено. Они также могут увидеть, было ли сообщение изменено злоумышленниками после его отправки..

Чтобы проверить цифровую подпись, получатель сначала использует ту же хеш-функцию, чтобы найти значение хеш-функции полученного сообщения. Получатель затем применяет открытый ключ отправителя к цифровой подписи, используя формулу шифрования (с = ме мод н), дать им хэш цифровой подписи.

По сравнение хеша сообщения, полученного вместе с хешем из зашифрованной цифровой подписи, получатель может сказать, является ли сообщение подлинным. Если два значения одинаковы, сообщение не было изменено с момента его подписания оригинальным отправителем. Если бы сообщение было изменено хотя бы одним символом, значение хеша было бы совершенно другим.

RSA безопасность & нападки

Как и большинство криптосистем, безопасность RSA зависит от того, как он реализован и используется. Одним из важных факторов является размер ключа. Чем больше битов в ключе (по сути, каков длина ключа), тем сложнее его взломать с помощью атак. такие как перебор и факторинг.

Поскольку алгоритмы асимметричного ключа, такие как RSA, могут быть нарушены целочисленной факторизацией, а алгоритмы симметричного ключа, такие как AES, не могут, ключи RSA должны быть намного длиннее, чтобы достичь того же уровня безопасности.

В настоящее время самый большой размер ключа, который был учтен, составляет 768 бит. Это было сделано командой ученых за два года, используя сотни машин.

Поскольку факторинг был завершен к концу 2009 года и вычислительная мощность значительно возросла с того времени, можно предположить, что попытка аналогичной интенсивности теперь может учитывать гораздо больший ключ RSA.

Несмотря на это, время и ресурсы, необходимые для такого рода атак, делают его недоступным для большинства хакеров и попадают в область национальных государств. Наилучшая длина ключа зависит от вашей индивидуальной модели угроз. Национальный институт стандартов и технологий рекомендует минимальный размер ключа 2048-бит, но 4096-битные ключи также используются в некоторых ситуациях, когда уровень угрозы выше.

Факторинг – это только один из способов, которым RSA может быть нарушена. Ряд других атак может нарушить шифрование с меньшим количеством ресурсов, но они зависят от реализации и других факторов, а не от самого RSA. Некоторые из них включают в себя:

Действительно ли простые числа случайны??

Некоторые реализации RSA используют слабые генераторы случайных чисел, чтобы придумать простые числа. Если эти числа не являются достаточно случайными, злоумышленникам будет намного проще их разложить и взломать шифрование. Эта проблема можно избежать с помощью криптографически безопасного генератора псевдослучайных чисел.

Плохая генерация ключей

Ключи RSA должны соответствовать определенным параметрам, чтобы обеспечить их безопасность. Если простые числа п и Q слишком близко друг к другу, ключ может быть легко обнаружен. Аналогично, число d который составляет часть закрытого ключа не может быть слишком маленьким. Низкое значение облегчает решение. Важно, чтобы эти цифры имели достаточную длину, чтобы сохранить ваш ключ в безопасности..

Атаки по побочным каналам

Это тип атаки, который не нарушает RSA напрямую, а использует информацию из своей реализации, чтобы дать злоумышленникам подсказки о процессе шифрования. Эти атаки могут включать в себя такие вещи, как анализируя количество энергии, которая используется, или анализ отраслевого прогноза, который использует измерения времени выполнения, чтобы обнаружить закрытый ключ.

Другой тип атаки по побочному каналу известен как временная атака. Если у злоумышленника есть возможность измерить время расшифровки на компьютере его цели для ряда различных зашифрованных сообщений, эта информация может позволить злоумышленнику определить личный ключ цели.

Большинство реализаций RSA избегают этой атаки, добавляя одноразовое значение во время процесса шифрования, что устраняет эту корреляцию. Этот процесс называется криптографическое ослепление.

Безопасно ли шифрование RSA на будущее??

Хорошей новостью является то, что RSA считается безопасным для использования, несмотря на эти возможные атаки. Предостережение в том, что это должно быть реализовано правильно и использовать ключ, который попадает в правильные параметры. Как мы только что обсудили, реализации, которые не используют заполнение, используют простые числа неадекватного размера или имеют другие уязвимости, нельзя считать безопасными.

Если вы хотите использовать шифрование RSA, убедитесь, что вы используете ключ не менее 1024 бит. Те, у кого более высокие модели угроз, должны придерживаться ключей длиной 2048 или 4096 бит, если они хотят использовать RSA с уверенностью. Если вы знаете о слабых сторонах RSA и используете его правильно, вы должны чувствовать себя в безопасности при использовании RSA для обмена ключами и других подобных задач, которые требуют шифрования с открытым ключом.

Смотрите также: Общие типы шифрования объяснены