การแลกเปลี่ยนคีย์ Diffie – Hellman คืออะไรและทำงานอย่างไร

การแลกเปลี่ยนคีย์ Diffie-Hellman คือ หนึ่งในการพัฒนาที่สำคัญที่สุดในการเข้ารหัสคีย์สาธารณะ และยังคงมีการใช้งานบ่อยครั้งในโปรโตคอลความปลอดภัยที่แตกต่างกันของวันนี้.

อนุญาตให้ทั้งสองฝ่ายที่ไม่เคยพบกันมาก่อนสามารถสร้างกุญแจที่พวกเขาสามารถใช้เพื่อรักษาความปลอดภัยการสื่อสารของพวกเขา ในบทความนี้เราจะอธิบายสิ่งที่มันใช้สำหรับวิธีการทำงานของมันทีละขั้นตอนรูปแบบที่แตกต่างกันของมันรวมทั้งข้อควรพิจารณาด้านความปลอดภัยที่จะต้องมีการบันทึกไว้เพื่อนำไปใช้อย่างปลอดภัย.

การแลกเปลี่ยนคีย์ Diffie-Hellman คืออะไร?

การแลกเปลี่ยนคีย์ Diffie-Hellman คือ วิธีการแรกที่ใช้กันอย่างแพร่หลายในการพัฒนาและแลกเปลี่ยนคีย์อย่างปลอดภัยผ่านช่องทางที่ไม่ปลอดภัย.

มันอาจดูไม่น่าตื่นเต้นหรือแปลกใหม่ในข้อตกลงข้างต้นดังนั้นขอยกตัวอย่างที่อธิบายว่าทำไมการแลกเปลี่ยนคีย์ Diffie-Hellman จึงเป็นเหตุการณ์สำคัญในโลกของการเข้ารหัสและทำไมจึงยังใช้บ่อยในปัจจุบัน.

สมมติว่าคุณเป็นสายลับลับสุดยอดและคุณต้องส่งข้อมูลสำคัญไปยังสำนักงานใหญ่ของคุณ. คุณจะป้องกันไม่ให้ศัตรูของคุณได้รับข้อความ?

ทางออกที่พบบ่อยที่สุดคือการเข้ารหัสข้อความด้วยรหัส วิธีที่ง่ายที่สุดคือการจัดเรียงรหัสและรหัสที่คุณต้องการใช้ล่วงหน้าหรือจัดทำผ่านช่องทางการสื่อสารที่ปลอดภัย.

สมมติว่าคุณเป็นสายลับที่ไม่ดีโดยเฉพาะและคุณและสำนักงานใหญ่ของคุณตัดสินใจที่จะใช้รหัสตัวเข้ารหัสที่อ่อนแอเพื่อเข้ารหัสข้อความของคุณ ในรหัสนี้ทุกคน “a” กลายเป็น “b” ทุกคน “b” กลายเป็น “c” ทุกคน “c” กลายเป็น “d” และต่อไปเรื่อย ๆ จนถึง “z” กลายเป็น “a”.

ภายใต้รหัสการเปลี่ยนแปลงนี้ข้อความ “มาทานอาหารเย็น” จะกลายเป็น “ไม่ได้เป็น hfu ejoofs” โชคดีที่ในสถานการณ์สมมุติของเราฝ่ายตรงข้ามของคุณไร้ความสามารถอย่างที่คุณเป็นและไม่สามารถถอดรหัสรหัสง่ายๆได้ซึ่งทำให้พวกเขาไม่สามารถเข้าถึงเนื้อหาของข้อความได้.

แต่จะเกิดอะไรขึ้นหากคุณไม่สามารถจัดการรหัสกับผู้รับล่วงหน้าได้?

สมมติว่าคุณต้องการสื่อสารกับสายลับจากประเทศพันธมิตรที่คุณไม่เคยพบมาก่อน คุณไม่มีช่องทางที่ปลอดภัยที่จะพูดคุยกับพวกเขา หากคุณไม่เข้ารหัสข้อความของคุณฝ่ายตรงข้ามที่สกัดกั้นข้อความนั้นจะสามารถอ่านเนื้อหาได้ หากคุณเข้ารหัสโดยไม่บอกรหัสพันธมิตรดังนั้นศัตรูจะไม่สามารถอ่านได้ แต่พันธมิตรจะไม่อ่าน.

ปัญหานี้เป็นหนึ่งใน conundrums ที่ใหญ่ที่สุดในการเข้ารหัสจนถึงปี 1970:

คุณจะแลกเปลี่ยนข้อมูลกับใครบางคนอย่างปลอดภัยได้อย่างไรหากคุณไม่มีโอกาสแบ่งปันรหัสล่วงหน้า?

การแลกเปลี่ยนคีย์ Diffie-Hellman เป็นกลไกแรกที่สาธารณชนใช้เพื่อแก้ไขปัญหานี้ อัลกอริทึมช่วยให้ผู้ที่ไม่เคยพบกันมาก่อนในการสร้างรหัสแชร์อย่างปลอดภัยแม้ผ่านช่องทางที่ไม่ปลอดภัยซึ่งฝ่ายตรงข้ามอาจเฝ้าดู.

ประวัติความเป็นมาของการแลกเปลี่ยนกุญแจ Diffie-Hellman

การแลกเปลี่ยนคีย์ Diffie-Hellman มีร่องรอยของรากกลับสู่ทศวรรษ 1970 ในขณะที่เขตข้อมูลของการเข้ารหัสได้พัฒนาอย่างมีนัยสำคัญตลอดศตวรรษที่ยี่สิบก่อนหน้าความก้าวหน้าเหล่านี้ส่วนใหญ่มุ่งเน้นไปที่พื้นที่ของการเข้ารหัสแบบสมมาตร – คีย์.

มันไม่ใช่จนกระทั่งปี 1976 ที่อัลกอริธึมกุญแจสาธารณะปรากฏในพื้นที่สาธารณะเมื่อ Whitfield Diffie และ Martin Hellman ตีพิมพ์บทความของพวกเขา, ทิศทางใหม่ในการเข้ารหัส. ความร่วมมือดังกล่าวได้อธิบายถึงกลไกที่อยู่เบื้องหลังระบบใหม่ซึ่งจะเป็นที่รู้จักในนาม การแลกเปลี่ยนคีย์ Diffie-Hellman.

งานชิ้นนี้ได้รับแรงบันดาลใจบางส่วนจากการพัฒนาก่อนหน้านี้โดย Ralph Merkle สิ่งที่เรียกว่า ปริศนาของ Merkle เกี่ยวข้องกับฝ่ายหนึ่งในการสร้างและส่งปริศนาการเข้ารหัสจำนวนหนึ่งไปยังอีกฝ่ายหนึ่ง ปริศนาเหล่านี้จะใช้ทรัพยากรการคำนวณพอสมควร.

ผู้รับจะสุ่มเลือกตัวต่อหนึ่งตัวเพื่อไขปริศนาแล้วใช้ความพยายามที่จำเป็นเพื่อทำให้เสร็จ. เมื่อไขปริศนาถูกแก้ไขแล้วตัวบ่งชี้และกุญแจเซสชันจะถูกเปิดเผยต่อผู้รับ. จากนั้นผู้รับจะส่งตัวระบุกลับไปยังผู้ส่งดั้งเดิมซึ่งช่วยให้ผู้ส่งทราบว่าปริศนาตัวใดที่ได้รับการแก้ไขแล้ว.

เนื่องจากผู้ส่งดั้งเดิมสร้างปริศนาตัวระบุทำให้พวกเขารู้ว่ากุญแจเซสชันใดที่ผู้รับค้นพบและทั้งสองฝ่ายสามารถใช้คีย์นี้เพื่อสื่อสารอย่างปลอดภัยยิ่งขึ้น หากผู้โจมตีกำลังฟังการโต้ตอบพวกเขาจะสามารถเข้าถึงปริศนาทั้งหมดรวมถึงตัวระบุที่ผู้รับส่งกลับไปยังผู้ส่งดั้งเดิม.

ตัวระบุไม่ได้บอกผู้โจมตีว่าจะใช้คีย์เซสชันใดดังนั้นวิธีที่ดีที่สุดในการถอดรหัสข้อมูลคือ แก้ปริศนาทั้งหมดเพื่อเปิดเผยคีย์เซสชั่นที่ถูกต้อง. เนื่องจากผู้โจมตีจะต้องไขปริศนาครึ่งหนึ่งโดยเฉลี่ยมันจึงยากที่พวกเขาจะค้นพบกุญแจมากกว่าที่เป็นของผู้รับ.

วิธีการนี้ให้ความปลอดภัยมากขึ้น แต่อยู่ไกลจากโซลูชันที่สมบูรณ์แบบ การแลกเปลี่ยนคีย์ Diffie-Hellman ใช้แนวคิดเหล่านี้บางอย่างและทำให้พวกเขามีความซับซ้อนมากขึ้นเพื่อสร้างวิธีการเข้ารหัสที่ปลอดภัยสำหรับการเข้ารหัสคีย์สาธารณะ.

แม้ว่ามันจะเป็นที่รู้จักกันในชื่อการแลกเปลี่ยนคีย์ Diffie-Hellman มาร์ตินเฮลแมนเสนอว่าอัลกอริธึมนั้นมีชื่อว่าการแลกเปลี่ยนคีย์ Diffie-Hellman-Merkle แทน.

มันเป็นความคิดของสาธารณชนว่า Merkle, Hellman และ Diffie เป็นคนแรกที่พัฒนารหัสลับสาธารณะจนกระทั่งปี 1997 เมื่อรัฐบาลอังกฤษได้ยกเลิกการจำแนกงานในช่วงต้นทศวรรษ 1970 โดย James Ellis, Clifford Cox และ Malcolm Williamson.

ปรากฎว่าทั้งสามคนมาพร้อมกับโครงการเข้ารหัสกุญแจสาธารณะครั้งแรกระหว่างปี 1969 และ 1973 แต่งานของพวกเขาถูกจัดประเภทเป็นเวลาสองทศวรรษ ดำเนินการภายใต้สำนักงานการสื่อสารของรัฐบาล (GCHQ) สำนักงานข่าวกรองของสหราชอาณาจักร.

การค้นพบของพวกเขาคืออัลกอริทึม RSA ดังนั้น Diffie, Hellman และ Merkle ยังคงเป็นคนแรกที่พัฒนาการแลกเปลี่ยนคีย์ Diffie-Hellman แต่ไม่ได้เป็นนักประดิษฐ์คนแรกของการเข้ารหัสคีย์สาธารณะ.

ใช้คีย์แลกเปลี่ยน Diffie-Hellman อยู่ที่ไหน?

วัตถุประสงค์หลักของการแลกเปลี่ยนคีย์ Diffie-Hellman คือการ พัฒนาความลับร่วมกันอย่างปลอดภัยที่สามารถใช้เพื่อรับคีย์ ปุ่มเหล่านี้สามารถใช้กับอัลกอริทึมแบบสมมาตรเพื่อส่งข้อมูลในลักษณะที่ได้รับการป้องกัน. อัลกอริทึมแบบสมมาตรมีแนวโน้มที่จะใช้ในการเข้ารหัสข้อมูลจำนวนมากเพราะมันมีประสิทธิภาพมากกว่าอัลกอริทึมกุญแจสาธารณะ.

ในทางเทคนิคแล้วการแลกเปลี่ยนคีย์ Diffie-Hellman สามารถใช้เพื่อสร้างคีย์สาธารณะและส่วนตัว อย่างไรก็ตามในทางปฏิบัติ RSA มีแนวโน้มที่จะใช้แทน นี่เป็นเพราะอัลกอริทึม RSA นั้นยังสามารถลงนามใบรับรองกุญแจสาธารณะในขณะที่การแลกเปลี่ยนคีย์ Diffie-Hellman ไม่ได้.

อัลกอริทึม ElGamal ซึ่งใช้อย่างหนักใน PGP นั้นขึ้นอยู่กับการแลกเปลี่ยนคีย์ Diffie-Hellman ดังนั้นโปรโตคอลใด ๆ ที่ใช้มันจะใช้งาน Diffie-Hellman ประเภทใดก็ได้.

เป็นหนึ่งในวิธีการทั่วไปในการแจกจ่ายกุญแจอย่างปลอดภัยการแลกเปลี่ยนคีย์ Diffie-Hellman คือ มีการใช้งานบ่อยในโปรโตคอลความปลอดภัยเช่น TLS, IPsec, SSH, PGP และอื่น ๆ อีกมากมาย. สิ่งนี้ทำให้เป็นส่วนสำคัญของการสื่อสารที่ปลอดภัยของเรา.

เป็นส่วนหนึ่งของโปรโตคอลเหล่านี้การแลกเปลี่ยนคีย์ Diffie-Hellman มักจะใช้เพื่อช่วยรักษาความปลอดภัยในการเชื่อมต่อของคุณไปยังเว็บไซต์เพื่อเข้าถึงคอมพิวเตอร์เครื่องอื่นจากระยะไกลและสำหรับการส่งอีเมลที่เข้ารหัส

การแลกเปลี่ยนคีย์ Diffie-Hellman ทำงานอย่างไร?

การแลกเปลี่ยนคีย์ Diffie-Hellman นั้นซับซ้อนและอาจเป็นเรื่องยากที่จะทำให้คุณรู้ว่ามันทำงานอย่างไร. มันใช้ตัวเลขขนาดใหญ่มากและคณิตศาสตร์จำนวนมาก, สิ่งที่พวกเราหลายคนยังคงกลัวจากบทเรียนมัธยมปลายที่น่าเบื่อและยาวนาน.

เพื่อให้เข้าใจง่ายขึ้น, เราจะเริ่มต้นด้วยการอธิบายการแลกเปลี่ยนคีย์ Diffie-Hellman ด้วยการเปรียบเทียบ. เมื่อคุณมีแนวคิดภาพใหญ่เกี่ยวกับวิธีการทำงานเราจะอธิบายรายละเอียดทางเทคนิคเพิ่มเติมเกี่ยวกับกระบวนการพื้นฐาน.

การเปรียบเทียบที่ดีที่สุดสำหรับโครงการ Diffie-Hellman คือการคิด คนสองคนกำลังผสมสี. มาใช้มาตรฐานการเข้ารหัสและบอกว่าชื่อของพวกเขาคืออลิซและบ๊อบ. พวกเขาทั้งสองเห็นด้วยกับสีแบบสุ่มเพื่อเริ่มต้น. สมมติว่าพวกเขาส่งข้อความถึงกันและ ตัดสินใจเกี่ยวกับสีเหลืองเป็นสีทั่วไป, เหมือนในแผนภาพด้านล่าง:

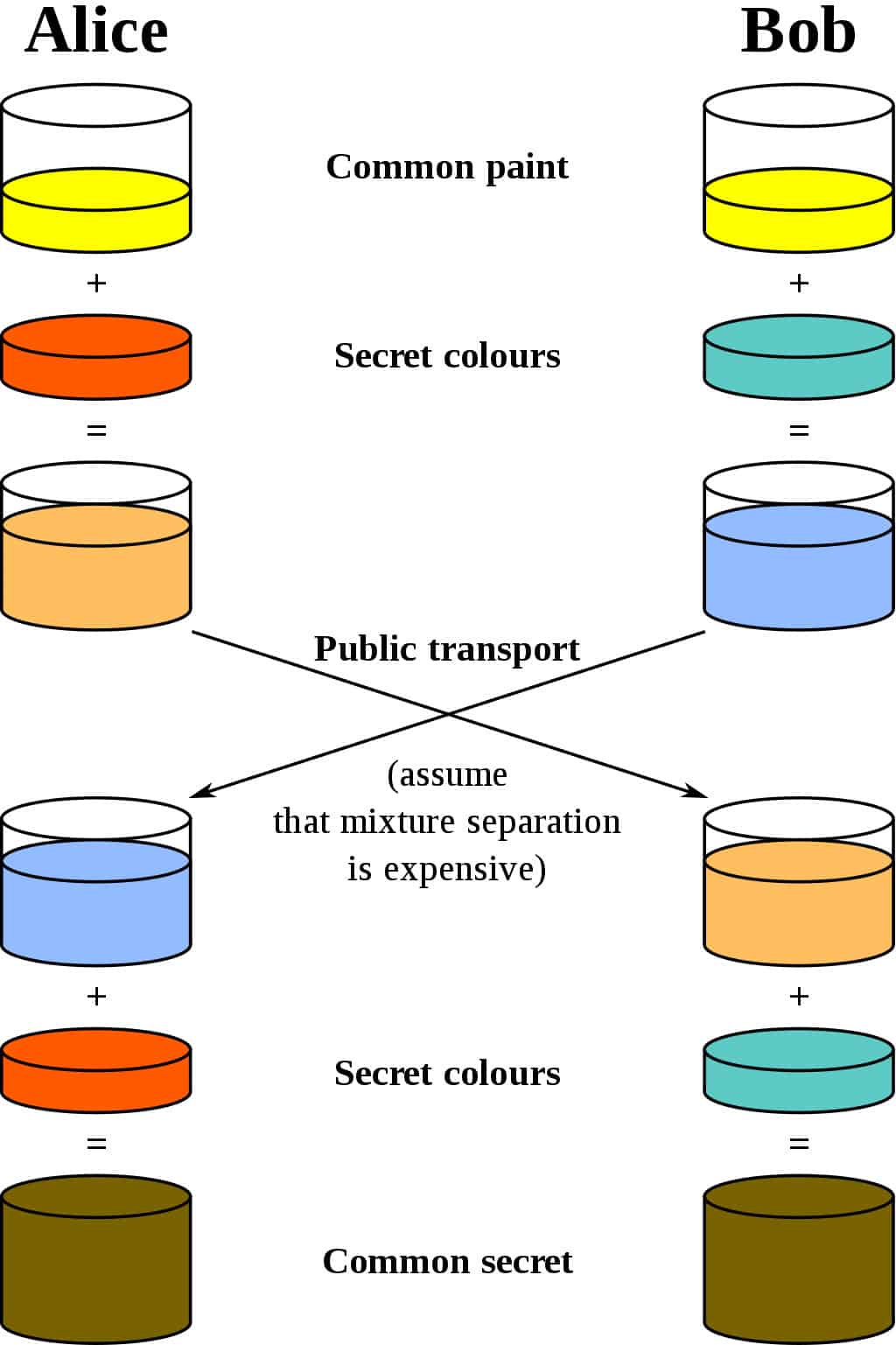
se สีลับของพวกเขาเอง พวกเขาไม่ได้บอกอีกฝ่ายว่าพวกเขาเลือก สมมติว่า Alice เลือก สีแดง, ในขณะที่บ๊อบเลือก สีน้ำเงินแกมเขียวเล็กน้อย.

ขั้นตอนต่อไปคือให้ทั้งอลิซและบ็อบผสมสีลับของพวกเขา (สีแดงสำหรับอลิซสีเขียวแกมน้ำเงินสำหรับบ๊อบ) ด้วยสีเหลืองที่พวกเขาตกลงร่วมกัน ตามแผนภาพ, อลิซลงท้ายด้วย ส้มโอ, ในขณะที่ผลลัพธ์ของ Bob คือ สีน้ำเงินเข้ม.

เมื่อพวกเขาผสมเสร็จแล้วพวกเขาก็ส่งผลให้อีกฝ่ายหนึ่ง. อลิซได้รับสีน้ำเงินที่ลึกกว่า, ในขณะที่ บ๊อบถูกส่งเป็นสีส้ม.

เมื่อพวกเขาได้รับผลผสมจากคู่ของพวกเขาพวกเขาก็เพิ่มสีลับของพวกเขาลงไป. อลิซใช้สีน้ำเงินที่ลึกกว่าและเพิ่มสีแดงที่เป็นความลับของเธอ, ในขณะที่ บ๊อบเพิ่มความลับสีเขียวแกมน้ำเงินของเขาลงในส่วนผสมสีส้มที่เขาเพิ่งได้รับ.

ผลลัพธ์? พวกเขาทั้งสองออกมาด้วยสีเดียวกัน, ซึ่งในกรณีนี้เป็นสีน้ำตาลน่าขยะแขยง มันอาจไม่ใช่สีแบบที่คุณต้องการทาสีห้องนั่งเล่นด้วย แต่มันก็เป็นสีที่ใช้ร่วมกัน สีที่ใช้ร่วมกันนี้เรียกว่า ความลับทั่วไป.

ส่วนที่สำคัญของการแลกเปลี่ยนคีย์ Diffie-Hellman คือทั้งสองฝ่ายจบลงด้วยผลลัพธ์เดียวกันโดยไม่จำเป็นต้องส่งความลับทั่วไปทั้งหมดผ่านช่องทางการสื่อสารทั้งหมด. การเลือกสีทั่วไปสีลับของตัวเองการแลกเปลี่ยนมิกซ์แล้วเพิ่มสีของตัวเองอีกครั้งทำให้ทั้งสองฝ่ายมีวิธีการที่จะมาถึงความลับทั่วไปที่เหมือนกันโดยไม่ต้องส่งสิ่งทั้งปวง.

หากผู้โจมตีกำลังฟังการแลกเปลี่ยนสิ่งที่พวกเขาสามารถเข้าถึงได้คือสีเหลืองทั่วไปที่อลิซและบ็อบเริ่มต้นด้วยเช่นเดียวกับสีผสมที่แลกเปลี่ยนกัน ตั้งแต่นี้จะทำจริงกับตัวเลขขนาดใหญ่แทนการทาสี, ข้อมูลเหล่านี้ไม่เพียงพอที่การโจมตีจะมองเห็นสีลับเริ่มต้นหรือความลับทั่วไป (ในทางเทคนิคเป็นไปได้ที่จะคำนวณความลับทั่วไปจากข้อมูลนี้ แต่ในการใช้งานการแลกเปลี่ยนคีย์ Diffie-Hellman อย่างปลอดภัยจะต้องใช้เวลาและทรัพยากรในการคำนวณที่ไม่สามารถทำได้).

โครงสร้างการแลกเปลี่ยนคีย์ Diffie-Hellman นี้เป็นสิ่งที่ทำให้มีประโยชน์มาก. อนุญาตให้ทั้งสองฝ่ายสื่อสารผ่านการเชื่อมต่อที่อาจเป็นอันตรายและยังคงเกิดขึ้นกับความลับร่วมที่พวกเขาสามารถใช้เพื่อสร้างคีย์การเข้ารหัสสำหรับการสื่อสารในอนาคต. ไม่สำคัญว่าผู้โจมตีคนใดที่กำลังฟังเพราะความลับที่ใช้ร่วมกันที่สมบูรณ์จะไม่ส่งผ่านการเชื่อมต่อ.

รายละเอียดทางเทคนิคของการแลกเปลี่ยนคีย์ Diffie-Hellman

ถึงเวลาสำหรับคณิตศาสตร์ …

ไม่ต้องกังวลเราจะทำให้ช้าลงและพยายามทำให้กระบวนการทั้งหมดเข้าใจง่ายที่สุดเท่าที่จะทำได้ มันเป็นไปตามสมมติฐานที่คล้ายคลึงกันตามที่แสดงด้านบน แต่แทนที่จะผสมและส่งสี, โครงการ Diffie-Hellman ทำให้การคำนวณจริงขึ้นอยู่กับจำนวนเฉพาะจำนวนมากพิเศษจากนั้นส่งพวกเขาข้าม.

เพื่อความปลอดภัยขอแนะนำว่า นายก (พี) มีความยาวอย่างน้อย 2,048 บิต, ซึ่งเทียบเท่าเลขฐานสองของจำนวนทศนิยมประมาณขนาดนี้:

415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019

เพื่อป้องกันไม่ให้หัวใคร ๆ เกิดการระเบิดเราจะเรียกใช้คำอธิบายนี้โดยใช้ตัวเลขที่น้อยกว่ามาก ระวังตัวด้วย การแลกเปลี่ยนคีย์ Diffie-Hellman จะไม่ปลอดภัยหากใช้ตัวเลขที่มีขนาดเล็กเท่าในตัวอย่างของเรา. เราใช้ตัวเลขเพียงเล็กน้อยเพื่อสาธิตแนวคิดในลักษณะที่เรียบง่ายขึ้น.

ในรูปแบบพื้นฐานที่สุดของการแลกเปลี่ยนกุญแจ Diffie-Hellman, อลิซและบ็อบเริ่มต้นด้วยการตัดสินใจร่วมกันโดยใช้ตัวเลขสองตัวเพื่อเริ่มต้น, ตรงข้ามกับสีทาเดี่ยวทั่วไปในตัวอย่างด้านบน เหล่านี้คือ โมดูลัสพี) และฐาน (ก.).

ในการใช้งานจริง, โมดูลัส (p) เป็นจำนวนเฉพาะที่มีขนาดใหญ่มาก, ในขณะที่ ฐาน (ก.) มีขนาดค่อนข้างเล็กเพื่อทำให้การคำนวณง่ายขึ้น. ฐาน (ก.) มาจากกลุ่มวงจร (G) ปกติแล้วจะถูกสร้างขึ้นอย่างดีก่อนที่ขั้นตอนอื่นจะเกิดขึ้น.

สำหรับตัวอย่างของเราสมมุติว่าโมดูลัสพี) คือ 17, ในขณะที่ฐาน (ก.) คือ 4.

เมื่อพวกเขาตัดสินใจร่วมกันเกี่ยวกับตัวเลขเหล่านี้แล้ว) สำหรับตัวเองในขณะที่บ๊อบเลือกหมายเลขลับของเขาเอง (ข) สมมติว่าพวกเขาเลือก:

a = 3

b = 6

อลิซก็ทำการคำนวณต่อไปนี้เพื่อให้หมายเลขที่เธอจะส่งถึง Bob:

A = ga mod p

ในการคำนวณข้างต้น, พอควร หมายถึงการดำเนินการแบบโมดูโล สิ่งเหล่านี้เป็นการคำนวณเพื่อหาส่วนที่เหลือหลังจากหารทางด้านซ้ายทางขวา ตัวอย่างเช่น:

15 mod 4 = 3

หากคุณเข้าใจวิธีการทำงานของโมดูโล่คุณสามารถทำได้ด้วยตนเองในการคำนวณต่อไปนี้มิฉะนั้นคุณสามารถใช้เครื่องคิดเลขออนไลน์ได้.

ดังนั้นให้เราใส่ตัวเลขลงในสูตร:

A = 43 mod 17

A = 64 mod 17

A = 13

เมื่อเราทำสิ่งเดียวกันกับบ็อบเราจะได้รับ:

B = 46 mod 17

B = 4096 mod 17

B = 16

อลิซก็ส่งผลให้เธอ () ถึง Bob ในขณะที่ Bob ส่งร่างของเขา (B) ถึงอลิซ อลิซจะคำนวณความลับที่แชร์ (s) ใช้หมายเลขที่เธอได้รับจาก Bob (B) และหมายเลขลับของเธอ () ใช้สูตรต่อไปนี้:

s = Ba mod พี

s = 163 mod 17

s = 4,096 mod 17

s = 16

บ๊อบก็ทำการคำนวณสิ่งเดียวกันโดยพื้นฐานแล้ว แต่ด้วยจำนวนที่อลิซส่งให้เขา () เช่นเดียวกับหมายเลขลับของเขา (ข):

s = ข พอควร พี

s = 136 mod 17

s = 4,826,809 mod 17

s = 16

อย่างที่คุณเห็นทั้งสองฝ่ายลงเอยด้วยผลลัพธ์เดียวกันสำหรับ s, 16. นี่เป็นความลับร่วมกันซึ่งมีเพียงอลิซและบ็อบเท่านั้นที่รู้ จากนั้นพวกเขาสามารถใช้สิ่งนี้เพื่อตั้งค่าคีย์สำหรับการเข้ารหัสแบบสมมาตรทำให้พวกเขาสามารถส่งข้อมูลระหว่างตัวเองอย่างปลอดภัยในแบบที่พวกเขาเท่านั้นที่สามารถเข้าถึงได้.

โปรดทราบว่าแม้ว่า B และ s เหมือนกันในตัวอย่างด้านบนนี่เป็นเพียงเรื่องบังเอิญจากจำนวนน้อยที่ถูกเลือกสำหรับภาพประกอบนี้ ปกติค่าเหล่านี้จะไม่เหมือนกันในการใช้งานจริงของการแลกเปลี่ยนคีย์ Diffie-Hellman.

แม้ว่าข้อมูลข้างต้นส่วนใหญ่จะถูกส่งข้ามช่องทางในรูปแบบข้อความธรรมดา (p, g, A และ B) และสามารถอ่านได้โดยผู้โจมตีที่อาจเป็นความลับที่ใช้ร่วมกัน (s) ไม่เคยส่ง มันจะไม่เป็นประโยชน์สำหรับผู้โจมตีในการคำนวณความลับที่ใช้ร่วมกันs) หรือตัวเลขลับอย่างใดอย่างหนึ่ง ( และ ข) จากข้อมูลที่ส่งเป็นข้อความธรรมดา.

แน่นอนว่าสมมติว่ามีการใช้การแลกเปลี่ยนคีย์ Diffie-Hellman อย่างเหมาะสมและมีการใช้จำนวนมากพอสมควร ตราบใดที่มีการปฏิบัติตามข้อกำหนดเหล่านี้การแลกเปลี่ยนคีย์ Diffie-Hellman ถือเป็นวิธีที่ปลอดภัยในการสร้างความลับร่วมซึ่งสามารถใช้เพื่อรักษาความปลอดภัยการสื่อสารในอนาคต.

การสร้างรหัสแชร์ระหว่างหลายฝ่าย

การแลกเปลี่ยนคีย์ Diffie-Hellman ยังสามารถใช้เพื่อตั้งค่าคีย์ที่แชร์กับผู้เข้าร่วมจำนวนมากขึ้น มันทำงานในลักษณะเดียวกันยกเว้นรอบต่อไปของการคำนวณที่จำเป็นสำหรับแต่ละฝ่ายในการเพิ่มหมายเลขลับของพวกเขาและจบลงด้วยความลับร่วมกัน.

เช่นเดียวกับในการแลกเปลี่ยนคีย์ Diffie-Hellman รุ่นสองบุคคลข้อมูลบางส่วนจะถูกส่งผ่านช่องทางที่ไม่ปลอดภัย แต่ไม่เพียงพอที่ผู้โจมตีจะสามารถคำนวณความลับที่แชร์ได้.

เหตุใดการแลกเปลี่ยนกุญแจ Diffie-Hellman จึงปลอดภัย?

ในระดับทางคณิตศาสตร์การแลกเปลี่ยนคีย์ Diffie-Hellman อาศัยฟังก์ชันทางเดียวเป็นพื้นฐานสำหรับความปลอดภัย สิ่งเหล่านี้คือการคำนวณซึ่งง่ายต่อการทำทางเดียว แต่ยากกว่าที่จะคำนวณในทางกลับกัน.

โดยเฉพาะอย่างยิ่งมันขึ้นอยู่กับปัญหา Diffie-Hellman ซึ่งถือว่าภายใต้พารามิเตอร์ที่เหมาะสมก็เป็นไปไม่ได้ในการคำนวณ ก.AB จากค่าที่แยกต่างหากของ ก., ก. และ ก.ข. ขณะนี้ยังไม่มีวิธีการที่สาธารณชนสามารถค้นพบได้ง่าย ก.AB จากค่าอื่น ๆ ซึ่งเป็นเหตุผลที่การแลกเปลี่ยนคีย์ Diffie-Hellman ถือว่าปลอดภัยแม้ว่าข้อเท็จจริงที่ว่าผู้โจมตีสามารถสกัดกั้นค่า พี, ก., , และ B.

การรับรอง & การแลกเปลี่ยนคีย์ Diffie-Hellman

ในโลกแห่งความเป็นจริงการแลกเปลี่ยนคีย์ Diffie-Hellman นั้นไม่ค่อยได้ใช้กัน เหตุผลหลักที่อยู่เบื้องหลังนี้คือ มันไม่มีการรับรองความถูกต้องซึ่งจะทำให้ผู้ใช้มีความเสี่ยงต่อการโจมตีจากคนกลาง.

การโจมตีเหล่านี้สามารถเกิดขึ้นได้เมื่อมีการแลกเปลี่ยนคีย์ Diffie-Hellman ด้วยตัวเองเพราะ มันไม่มีวิธีการตรวจสอบว่าอีกฝ่ายในการเชื่อมต่อเป็นจริงที่พวกเขาพูดว่าพวกเขาเป็น. ไม่มีรูปแบบการตรวจสอบใด ๆ, ผู้ใช้อาจกำลังเชื่อมต่อกับผู้โจมตี เมื่อพวกเขาคิดว่าพวกเขากำลังสื่อสารกับบุคคลที่เชื่อถือได้.

ด้วยเหตุนี้การแลกเปลี่ยนคีย์ Diffie-Hellman จึงถูกนำไปใช้ควบคู่กับการรับรองความถูกต้อง สิ่งนี้มักเกี่ยวข้องกับการใช้ใบรับรองดิจิทัลและอัลกอริทึมกุญแจสาธารณะเช่น RSA เพื่อตรวจสอบตัวตนของแต่ละฝ่าย.

รูปแบบของการแลกเปลี่ยนคีย์ Diffie-Hellman

การแลกเปลี่ยนคีย์ Diffie-Hellman สามารถนำไปใช้ได้หลายวิธีและยังเป็นพื้นฐานสำหรับอัลกอริทึมอื่น ๆ อีกมากมาย การนำไปใช้งานบางส่วนเหล่านี้ให้การอนุญาตในขณะที่คุณสมบัติอื่น ๆ มีการเข้ารหัสลับต่าง ๆ เช่นการส่งต่อความลับที่สมบูรณ์แบบ.

รูปไข่รูปโค้ง Diffie-Hellman

Diffie-Hellman ใช้กับโครงสร้างเชิงพีชคณิตของส่วนโค้งวงรีเพื่อให้การนำไปใช้งานเพื่อให้เกิดความปลอดภัยในระดับใกล้เคียงกับขนาดของคีย์ที่เล็กลง คีย์รูปไข่โค้ง 224 บิตให้ความปลอดภัยระดับเดียวกันกับคีย์ RSA 2048 บิต สิ่งนี้สามารถทำให้การแลกเปลี่ยนมีประสิทธิภาพมากขึ้นและลดข้อกำหนดด้านการจัดเก็บ.

นอกเหนือจากความยาวคีย์ที่เล็กลงและความจริงที่ว่ามันขึ้นอยู่กับคุณสมบัติของเส้นโค้งรูปไข่, รูปไข่ – โค้ง Diffie-Hellman ทำงานในลักษณะที่คล้ายคลึงกับการแลกเปลี่ยนคีย์ Diffie-Hellman มาตรฐาน.

TLS   

TLS ซึ่งเป็นโปรโตคอลที่ใช้ในการรักษาความปลอดภัยของอินเทอร์เน็ตส่วนใหญ่สามารถใช้การแลกเปลี่ยน Diffie-Hellman ในสามวิธีที่แตกต่างกัน: ไม่ระบุชื่อคงที่และชั่วคราว ในทางปฏิบัติควรมีการติดตั้ง Diffie-Hellman แบบชั่วคราวเท่านั้นเนื่องจากตัวเลือกอื่นมีปัญหาด้านความปลอดภัย.

• Diffie-Hellman นิรนาม – การแลกเปลี่ยนคีย์ Diffie-Hellman รุ่นนี้ไม่ได้ใช้การพิสูจน์ตัวตนใด ๆ ทำให้ไม่เสี่ยงต่อการถูกโจมตีจากคนกลาง ไม่ควรใช้หรือนำไปใช้.
• สถิต Diffie-Hellman – Static Diffie-Hellman ใช้ใบรับรองเพื่อตรวจสอบสิทธิ์เซิร์ฟเวอร์ มันไม่ได้ตรวจสอบลูกค้าโดยค่าเริ่มต้นและไม่ให้ส่งต่อความลับ.
• ชั่วคราว Diffie-Hellman – นี่ถือเป็นการใช้งานที่ปลอดภัยที่สุดเพราะมันให้ความลับส่งต่อที่สมบูรณ์แบบ โดยทั่วไปแล้วจะรวมกับอัลกอริทึมเช่น DSA หรือ RSA เพื่อตรวจสอบสิทธิ์ฝ่ายหนึ่งหรือทั้งสองฝ่ายในการเชื่อมต่อ Ephemeral Diffie-Hellman ใช้คู่คีย์ที่แตกต่างกันในแต่ละครั้งที่มีการเรียกใช้โปรโตคอล สิ่งนี้จะช่วยให้การเชื่อมต่อเป็นความลับที่สมบูรณ์แบบเพราะแม้ว่ากุญแจจะถูกบุกรุกในอนาคตมันไม่สามารถนำมาใช้เพื่อถอดรหัสข้อความที่ผ่านมาทั้งหมดได้.

ElGamal

ElGamal เป็นอัลกอริทึมกุญแจสาธารณะที่สร้างขึ้นจากการแลกเปลี่ยนคีย์ Diffie-Hellman เช่นเดียวกับ Diffie-Hellman ไม่มีข้อกำหนดสำหรับการตรวจสอบสิทธิ์ด้วยตนเองและโดยทั่วไปจะรวมเข้ากับกลไกอื่น ๆ เพื่อจุดประสงค์นี้.

ElGamal ส่วนใหญ่จะใช้ใน PGP, GNU Privacy Guard และระบบอื่น ๆ เนื่องจากคู่แข่งหลักของมันคือ RSA ซึ่งได้รับการจดสิทธิบัตร สิทธิบัตรของ RSA หมดอายุในปี 2000 ซึ่งอนุญาตให้นำไปใช้ได้อย่างอิสระหลังจากวันที่ดังกล่าว ตั้งแต่นั้นมา ElGamal ก็ยังไม่ถูกนำมาใช้บ่อย.

เอสที

โปรโตคอล Station-to-Station (STS) ยังใช้การแลกเปลี่ยนคีย์ Diffie-Hellman เป็นรูปแบบข้อตกลงที่สำคัญอีกอย่างหนึ่งอย่างไรก็ตามมันให้การป้องกันการโจมตีจากคนกลางและความลับที่สมบูรณ์แบบ.

มันต้องมีทั้งสองฝ่ายในการเชื่อมต่อเพื่อให้มีคู่กุญแจซึ่งใช้ในการตรวจสอบแต่ละด้าน หากทั้งสองฝ่ายไม่รู้จักกันดังนั้นสามารถใช้ใบรับรองเพื่อตรวจสอบตัวตนของทั้งสองฝ่าย.

การแลกเปลี่ยนคีย์ Diffie-Hellman & อาร์เอส

อย่างที่เราได้กล่าวไปก่อนหน้านี้, การแลกเปลี่ยนคีย์ Diffie-Hellman มักใช้ร่วมกับ RSA หรืออัลกอริธึมอื่น ๆ เพื่อให้การรับรองความถูกต้องสำหรับการเชื่อมต่อ. หากคุณคุ้นเคยกับ RSA คุณอาจสงสัย ทำไมทุกคนถึงต้องใช้การแลกเปลี่ยนคีย์ Diffie-Hellman เช่นกัน, เนื่องจาก RSA ช่วยให้บุคคลที่ไม่เคยพบกันมาก่อนสามารถสื่อสารได้อย่างปลอดภัย.

RSA อนุญาตให้ผู้ใช้เข้ารหัสข้อความด้วยพับลิกคีย์ของผู้ติดต่อเพื่อให้สามารถถอดรหัสได้โดยคีย์ส่วนตัวที่ตรงกันเท่านั้น อย่างไรก็ตามในทางปฏิบัติ, RSA ไม่ได้ใช้เข้ารหัสการสื่อสารทั้งหมดสิ่งนี้จะไม่มีประสิทธิภาพมากเกินไป.

แต่ RSA มักจะใช้เป็นวิธีการตรวจสอบสิทธิ์ทั้งสองฝ่ายแทน มันทำเช่นนี้กับ ใบรับรองดิจิทัลของแต่ละฝ่ายซึ่งจะได้รับการตรวจสอบโดยหน่วยงานผู้ออกใบรับรอง เพื่อพิสูจน์ว่าเจ้าของใบรับรองเป็นใครจริง ๆ ที่พวกเขาบอกว่าพวกเขาเป็นและกุญแจสาธารณะในใบรับรองจริงเป็นของพวกเขา.

สำหรับการรับรองความถูกต้องซึ่งกันและกัน, แต่ละฝ่ายจะลงนามข้อความโดยใช้คีย์ส่วนตัวของพวกเขาแล้วส่งไปยังพันธมิตรการสื่อสารของพวกเขา. ผู้รับแต่ละคนสามารถ ยืนยันตัวตนของอีกฝ่ายโดยการตรวจสอบข้อความที่ลงนามกับกุญแจสาธารณะในใบรับรองดิจิตอลของพันธมิตรการสื่อสาร (ดูบทความที่กล่าวถึงบน RSA สำหรับรายละเอียดเพิ่มเติมเกี่ยวกับวิธีการทำงานโดยเฉพาะอย่างยิ่ง การเซ็นข้อความ มาตรา).

ตอนนี้ทั้งสองฝ่ายได้รับการรับรองความถูกต้องแล้วก็เป็นไปได้ในทางเทคนิคที่จะใช้ RSA ต่อไปเพื่อส่งข้อความที่เข้ารหัสลับอย่างปลอดภัยระหว่างกัน.

เพื่อหลีกเลี่ยงความไร้ประสิทธิภาพนี้โปรโตคอลความปลอดภัยจำนวนมากใช้อัลกอริทึมเช่น การแลกเปลี่ยนคีย์ Diffie-Hellman จะเกิดขึ้นกับความลับทั่วไปที่สามารถใช้เพื่อสร้างคีย์ symmetric ที่ใช้ร่วมกัน. คีย์สมมาตรนี้จะใช้ในอัลกอริทึมคีย์ – สมมาตรเช่น AES เพื่อเข้ารหัสข้อมูล ที่ทั้งสองฝ่ายตั้งใจจะส่งระหว่างกันอย่างปลอดภัย.

มันอาจดูเหมือนเป็นกระบวนการที่ซับซ้อนและซับซ้อน แต่มันกลับกลายเป็นทรัพยากรที่รวดเร็วและเรียกร้องน้อยกว่าเมื่อเปรียบเทียบกับการใช้อัลกอริทึมกุญแจสาธารณะสำหรับการแลกเปลี่ยนทั้งหมด นี้เป็นเพราะ การเข้ารหัสคีย์สมมาตรเป็นคำสั่งที่มีประสิทธิภาพมากกว่าการเข้ารหัสคีย์สาธารณะ.

นอกเหนือจากความไร้ประสิทธิภาพที่เราเพิ่งพูดถึงมีข้อเสียอื่น ๆ ที่มาจากการใช้ RSA เพียงอย่างเดียว. RSA ต้องการช่องว่างภายในเพื่อให้ปลอดภัย, ดังนั้นอัลกอริทึมเพิ่มเติมจะต้องดำเนินการอย่างเหมาะสมควบคู่ไปกับมันเพื่อให้ปลอดภัย.

RSA ไม่มีการส่งต่อความลับที่สมบูรณ์แบบ, อย่างใดอย่างหนึ่งซึ่งเป็นข้อเสียอื่นเมื่อเปรียบเทียบกับการแลกเปลี่ยนคีย์ Diffie-Hellman ephemeral โดยรวมเหตุผลเหล่านี้เป็นเหตุผลว่าทำไมในหลาย ๆ สถานการณ์จึงเป็นการดีที่สุดที่จะใช้ RSA ร่วมกับการแลกเปลี่ยนคีย์ Diffie-Hellman เท่านั้น.

อีกทางหนึ่งการแลกเปลี่ยนคีย์ Diffie-Hellman สามารถรวมกับอัลกอริทึมเช่น Digital Signature Standard (DSS) เพื่อให้การรับรองความถูกต้องการแลกเปลี่ยนคีย์การรักษาความลับและตรวจสอบความสมบูรณ์ของข้อมูล ในสถานการณ์เช่นนี้ RSA ไม่จำเป็นสำหรับการเชื่อมต่อที่ปลอดภัย.

ปัญหาด้านความปลอดภัยของการแลกเปลี่ยนคีย์ Diffie-Hellman

ความปลอดภัยของการแลกเปลี่ยนคีย์ Diffie-Hellman นั้นขึ้นอยู่กับวิธีการนำไปใช้งานรวมถึงหมายเลขที่เลือกไว้ ดังที่เราได้กล่าวไว้ข้างต้นมันไม่ได้มีวิธีการรับรองความถูกต้องของอีกฝ่าย แต่ในทางปฏิบัติมีการใช้กลไกอื่นเพื่อให้แน่ใจว่าอีกฝ่ายในการเชื่อมต่อไม่ใช่ผู้หลอกลวง.

พารามิเตอร์สำหรับการเลือกหมายเลข

หากการใช้งานการแลกเปลี่ยนคีย์ Diffie-Hellman ในโลกแห่งความเป็นจริงนั้นใช้ตัวเลขเพียงเล็กน้อยในตัวอย่างของเรามันจะทำให้กระบวนการแลกเปลี่ยนเป็นเรื่องเล็กน้อยสำหรับผู้โจมตีที่จะร้าว แต่ไม่ใช่ขนาดของตัวเลขที่สำคัญ – ตัวเลขนั้นต้องสุ่มอย่างเพียงพอ หากตัวสร้างตัวเลขสุ่มสร้างเอาต์พุตที่สามารถคาดเดาได้มันสามารถทำลายความปลอดภัยของการแลกเปลี่ยนคีย์ Diffie-Hellman ได้อย่างสมบูรณ์.

จำนวน พี ควรมีความยาว 2048 บิต เพื่อความปลอดภัย. ฐาน, ก., อาจมีจำนวนค่อนข้างน้อยเช่น 2, แต่มันต้องมาจากคำสั่งของ G ที่มีปัจจัยสำคัญขนาดใหญ่

การโจมตี Logjam

การแลกเปลี่ยนคีย์ Diffie-Hellman ได้รับการออกแบบบนพื้นฐานของปัญหาลอการิทึมแบบแยกซึ่งยากต่อการแก้ไข. กลไกที่รู้จักกันทั่วไปที่มีประสิทธิภาพที่สุดสำหรับการค้นหาวิธีแก้ปัญหาคืออัลกอริทึมตะแกรงฟิลด์หมายเลข.

ความสามารถของอัลกอริทึมนี้ถูกนำมาพิจารณาเมื่อการแลกเปลี่ยนคีย์ Diffie-Hellman ได้รับการออกแบบ ภายในปี 1992 เป็นที่ทราบกันดีว่าสำหรับกลุ่มที่กำหนด, G, สามในสี่ขั้นตอนที่เกี่ยวข้องกับอัลกอริทึมสามารถคำนวณได้ล่วงหน้า หากความคืบหน้านี้ถูกบันทึกไว้ขั้นตอนสุดท้ายสามารถคำนวณได้ในเวลาอันสั้น.

สิ่งนี้ก็ไม่ได้เกี่ยวข้องด้วยเช่นกันจนกว่าจะทราบว่าส่วนสำคัญของการรับส่งข้อมูลอินเทอร์เน็ตใช้กลุ่มเดียวกันกับ 1024 บิตหรือเล็กกว่า ในปี 2558 ทีมวิชาการเรียกใช้การคำนวณสำหรับไพรม์ 512 บิตที่ใช้บ่อยที่สุดโดยการแลกเปลี่ยนคีย์ Diffie-Hellman ใน TLS.

พวกเขายังสามารถปรับลดเซิร์ฟเวอร์ 80% ของ TLS ที่รองรับ DHE-EXPORT เพื่อให้พวกเขายอมรับการแลกเปลี่ยนคีย์ Diffie-Hellman เกรดส่งออก 512 บิตสำหรับการเชื่อมต่อ ซึ่งหมายความว่า เซิร์ฟเวอร์เหล่านี้แต่ละเครื่องมีความเสี่ยงต่อการถูกโจมตีจากฝ่ายตรงข้ามที่มีทรัพยากรเพียงพอ.

นักวิจัยทำการประเมินผลของพวกเขา, การประเมินว่ารัฐชาติอาจทำลายนายกที่ 1024 บิตได้. ด้วยการทำลายไพรเมอร์ที่ใช้กันมากที่สุดเพียง 1024 บิตเดียวทีมวิชาการประเมินว่าฝ่ายตรงข้ามสามารถติดตาม 18% ของเว็บไซต์ HTTPS ยอดนิยมหนึ่งล้าน.

พวกเขากล่าวต่อไปว่านายกที่สองจะช่วยให้ฝ่ายตรงข้ามสามารถถอดรหัสการเชื่อมต่อเซิร์ฟเวอร์ VPN ได้ 66% และ 26% ของเซิร์ฟเวอร์ SSH ต่อมาในรายงานนักวิชาการแนะนำว่า NSA อาจมีความสามารถเหล่านี้แล้ว.

“ การอ่านการรั่วไหลของ NSA อย่างใกล้ชิดแสดงให้เห็นว่าการโจมตีของ VPN ในหน่วยงานสอดคล้องกับการหยุดพักเช่นนี้”

แม้จะมีช่องโหว่นี้การแลกเปลี่ยนคีย์ Diffie-Hellman ยังคงปลอดภัยหากใช้งานอย่างถูกต้อง ตราบใดที่มีการใช้คีย์ 2048 บิตการโจมตี Logjam จะไม่ทำงาน เบราว์เซอร์ที่อัปเดตนั้นปลอดภัยจากการโจมตีนี้.

การแลกเปลี่ยนคีย์ Diffie-Hellman นั้นปลอดภัยหรือไม่?

แม้ว่าการแลกเปลี่ยนคีย์ Diffie-Hellman อาจดูซับซ้อน แต่เป็นส่วนพื้นฐานของการแลกเปลี่ยนข้อมูลออนไลน์อย่างปลอดภัย ตราบใดที่มีการใช้งานควบคู่ไปกับวิธีการตรวจสอบความถูกต้องที่เหมาะสมและมีการเลือกหมายเลขอย่างถูกต้องจะไม่ถือว่ามีความเสี่ยงต่อการถูกโจมตี.

การแลกเปลี่ยนคีย์ Diffie-Hellman เป็นวิธีการใหม่ที่ช่วยให้ทั้งสองฝ่ายที่ไม่รู้จักติดต่อกันได้อย่างปลอดภัยเมื่อมันถูกพัฒนาขึ้นในปี 1970 ขณะนี้เราใช้เวอร์ชันใหม่กว่าพร้อมกับปุ่มที่ใหญ่กว่าเพื่อป้องกันเทคโนโลยีที่ทันสมัย โปรโตคอลเองดูเหมือนว่าจะยังคงปลอดภัยจนกว่าจะถึงการคำนวณควอนตัม และการโจมตีขั้นสูงที่จะมาพร้อมกับมัน.

เทคโนโลยีธุรกิจความปลอดภัยทางไซเบอร์ โดย TheDigitalArtist ได้รับอนุญาตภายใต้ มอนส์ CC0