
Schimbul de chei Diffie-Hellman a fost una dintre cele mai importante evoluții în criptografia cu cheie publică și este încă în mod frecvent implementat într-o serie de protocoale de securitate diferite de astăzi.
Acesta permite două părți care nu s-au întâlnit anterior să stabilească în siguranță o cheie pe care o pot folosi pentru a-și asigura comunicarea. În acest articol, vă vom explica pentru ce este folosit, cum funcționează pas cu pas, diferitele variații ale acesteia, precum și considerațiile de securitate care trebuie notate pentru a-l implementa în siguranță.
Care este schimbul de chei Diffie-Hellman?
Schimbul de chei Diffie-Hellman a fost prima metodă utilizată pe scară largă de a dezvolta și schimba în siguranță cheile pe un canal nesigur.
Este posibil să nu pară atât de interesant sau de revoltă în termenii de mai sus, așa că să oferim un exemplu care să explice de ce schimbul de chei Diffie-Hellman a fost o etapă atât de importantă în lumea criptografiei și de ce este încă utilizat atât de frecvent astăzi.
Să spunem că sunteți un spion de top secret și trebuie să trimiteți informații importante la sediul central. Cum i-ai putea împiedica pe dușmani să nu apară mesajul?
Cea mai comună soluție ar fi să criptați mesajul cu un cod. Cel mai simplu mod este de a aranja oricare dintre tipurile de cod și cheie pe care intenționați să le utilizați în prealabil sau de a le face pe un canal de comunicare sigur.
Să spunem că sunteți un spion deosebit de rău, iar dvs. și sediul central vă hotărâți să folosiți un schimbător slab pentru a codifica mesajele. În acest cod, fiecare „a” devine „b”, fiecare „b” devine „c”, fiecare „c” devine „d” și așa mai departe, până la „z” devenind „a”.
În cadrul acestei cifre de schimb, mesajul „Să luăm cina” devine „Mfu’s hfu ejoofs”. Din fericire, în situația noastră ipotetică, adversarii tăi sunt la fel de incompetenți precum și nu sunt capabili să crape un astfel de cod simplu, care îi împiedică să acceseze conținutul mesajului.
Dar ce se întâmplă dacă nu ați putea aranja un cod cu destinatarul dinainte?
Să presupunem că doriți să comunicați cu un spion dintr-o națiune aliată pe care nu ați întâlnit-o niciodată. Nu aveți un canal sigur pe care să le vorbiți. Dacă nu criptați mesajul dvs., orice adversar care îl interceptează va putea citi conținutul. Dacă îl criptați fără a spune aliatului codul, atunci inamicul nu va putea să-l citească, dar nici aliatul nu îl va putea citi.
Această problemă a fost una dintre cele mai mari conundrums în criptografie până în anii ’70:
Cum puteți schimba informații în siguranță cu cineva dacă nu ați avut ocazia să împărtășiți cheia înainte de timp?
Schimbul de chei Diffie-Hellman a fost primul mecanism utilizat public pentru rezolvarea acestei probleme. Algoritmul le permite celor care nu s-au întâlnit până acum să creeze în siguranță o cheie partajată, chiar și pe un canal nesigur pe care adversarii ar putea să-l monitorizeze.
Istoria schimbului de chei Diffie-Hellman
Schimbul de chei Diffie-Hellman își trage rădăcinile încă din anii ’70. În timp ce domeniul criptografiei s-a dezvoltat semnificativ pe parcursul secolului XX, aceste progrese au fost concentrate în principal în zona criptografiei cu cheie simetrică..
Abia în 1976 au apărut algoritmi cheie publică în sfera publică, când Whitfield Diffie și Martin Hellman au publicat lucrarea lor, Noi direcții în criptografie. Colaborarea a evidențiat mecanismele din spatele unui nou sistem, care va fi cunoscut sub numele de Schimb de chei Diffie-Hellman.
Lucrarea a fost parțial inspirată de evoluțiile anterioare realizate de Ralph Merkle. Asa numitul Merkle’s Puzzle implică o parte crearea și trimiterea unui număr de puzzle-uri criptografice celeilalte. Aceste puzzle-uri ar trebui să rezolve o cantitate moderată de resurse de calcul.
Destinatarul ar alege la întâmplare un puzzle de rezolvat și apoi ar cheltui efortul necesar pentru completarea acestuia. După ce puzzle-ul este rezolvat, un identificator și o cheie de sesiune sunt dezvăluite destinatarului. Destinatarul transmite identificatorul înapoi expeditorului inițial, ceea ce îi permite expeditorului să știe ce puzzle a fost rezolvat.
Deoarece expeditorul inițial a creat puzzle-urile, identificatorul le anunță ce cheie de sesiune a descoperit destinatarul, iar cele două părți pot utiliza această cheie pentru a comunica mai sigur. Dacă un atacator ascultă interacțiunea, acesta va avea acces la toate puzzle-urile, precum și identificatorul pe care destinatarul îl transmite expeditorului inițial.
Identificatorul nu spune atacatorului ce cheie de sesiune este folosită, deci cea mai bună abordare pentru decriptarea informațiilor este să rezolvați toate puzzle-urile pentru a descoperi cheia corectă a sesiunii. Având în vedere că atacatorul va trebui să rezolve în medie jumătate din puzzle-uri, acesta ajunge să fie mult mai dificil pentru a descoperi cheia decât pentru destinatar..
Această abordare oferă mai multă securitate, dar este departe de o soluție perfectă. Schimbul de chei Diffie-Hellman a luat unele dintre aceste idei și le-a făcut mai complexe pentru a crea o metodă sigură de criptografie cu chei publice..
Deși a devenit cunoscut sub numele de schimbul de chei Diffie-Hellman, Martin Hellman a propus ca algoritmul să fie numit schimbul de chei Diffie-Hellman-Merkle în schimb, pentru a reflecta munca pe care Ralph Merkle a depus-o în fața criptografiei cu chei publice..
S-a crezut public că Merkle, Hellman și Diffie au fost primii oameni care au dezvoltat criptografia cu chei publice până în 1997, când Guvernul britanic a declasificat lucrările efectuate la începutul anilor ’70 de către James Ellis, Clifford Cox și Malcolm Williamson.
Se dovedește că trio-ul a venit cu prima schemă de criptare a cheilor publice între 1969 și 1973, dar munca lor a fost clasificată timp de două decenii. Acesta a fost realizat sub sediul Guvernării Comunicării (GCHQ), o agenție de informații din Marea Britanie.
Descoperirea lor a fost de fapt algoritmul RSA, astfel că Diffie, Hellman și Merkle au fost încă primii care au dezvoltat schimbul de chei Diffie-Hellman, dar nu mai au fost primii inventatori ai criptografiei cu chei publice..
Unde se utilizează schimbul de chei Diffie-Hellman?
Principalul scop al schimbului de chei Diffie-Hellman este să dezvoltați în siguranță secrete partajate care pot fi folosite pentru a obține chei. Aceste taste pot fi apoi utilizate cu algoritmi cu cheie simetrică pentru a transmite informații într-o manieră protejată. Algoritmii simetrici tind să fie folosiți pentru a cripta cea mai mare parte a datelor, deoarece sunt mai eficienți decât algoritmii cu chei publice.
Tehnic, schimbul de chei Diffie-Hellman poate fi utilizat pentru a stabili chei publice și private. Cu toate acestea, în practică, RSA tinde să fie utilizat în schimb. Acest lucru se datorează faptului că algoritmul RSA este, de asemenea, capabil să semneze certificate cu cheie publică, în timp ce schimbul de chei Diffie-Hellman nu este.
Algoritmul ElGamal, care a fost utilizat foarte mult în PGP, se bazează pe schimbul de chei Diffie-Hellman, astfel că orice protocol care îl folosește implementează eficient un fel de Diffie-Hellman.
Ca una dintre cele mai frecvente metode pentru distribuirea în siguranță a cheilor, schimbul de chei Diffie-Hellman este implementate frecvent în protocoale de securitate precum TLS, IPsec, SSH, PGP și multe altele. Aceasta face parte integrantă a comunicațiilor noastre sigure.
Ca parte a acestor protocoale, schimbul de chei Diffie-Hellman este adesea folosit pentru a vă asigura conexiunea la un site web, pentru a accesa de la distanță un alt computer și pentru a trimite e-mailuri criptate.
Cum funcționează schimbul de chei Diffie-Hellman?
Schimbul de chei Diffie-Hellman este complex și poate fi dificil să îți atragi capul în jurul modului în care funcționează. Folosește un număr foarte mare și o mulțime de matematică, lucru pe care mulți dintre noi încă îl temem de la acele lungi și plictisitoare lecții de liceu.
Pentru a face lucrurile un pic mai ușor de înțeles, vom începe prin a explica schimbul de chei Diffie-Hellman cu o analogie. După ce aveți o idee ilustrată cu privire la modul în care funcționează, vom trece la o descriere mai tehnică a proceselor de bază.
Cea mai bună analogie pentru schema Diffie-Hellman este să te gândești două persoane amestecând vopseaua. Să folosim standardul de criptografie și să spunem că numele lor sunt Alice și Bob. Amândoi sunt de acord cu o culoare aleatorie cu care să înceapă. Să spunem că își transmit un mesaj reciproc și decide asupra galbenului ca culoare comună, la fel ca în diagrama de mai jos:
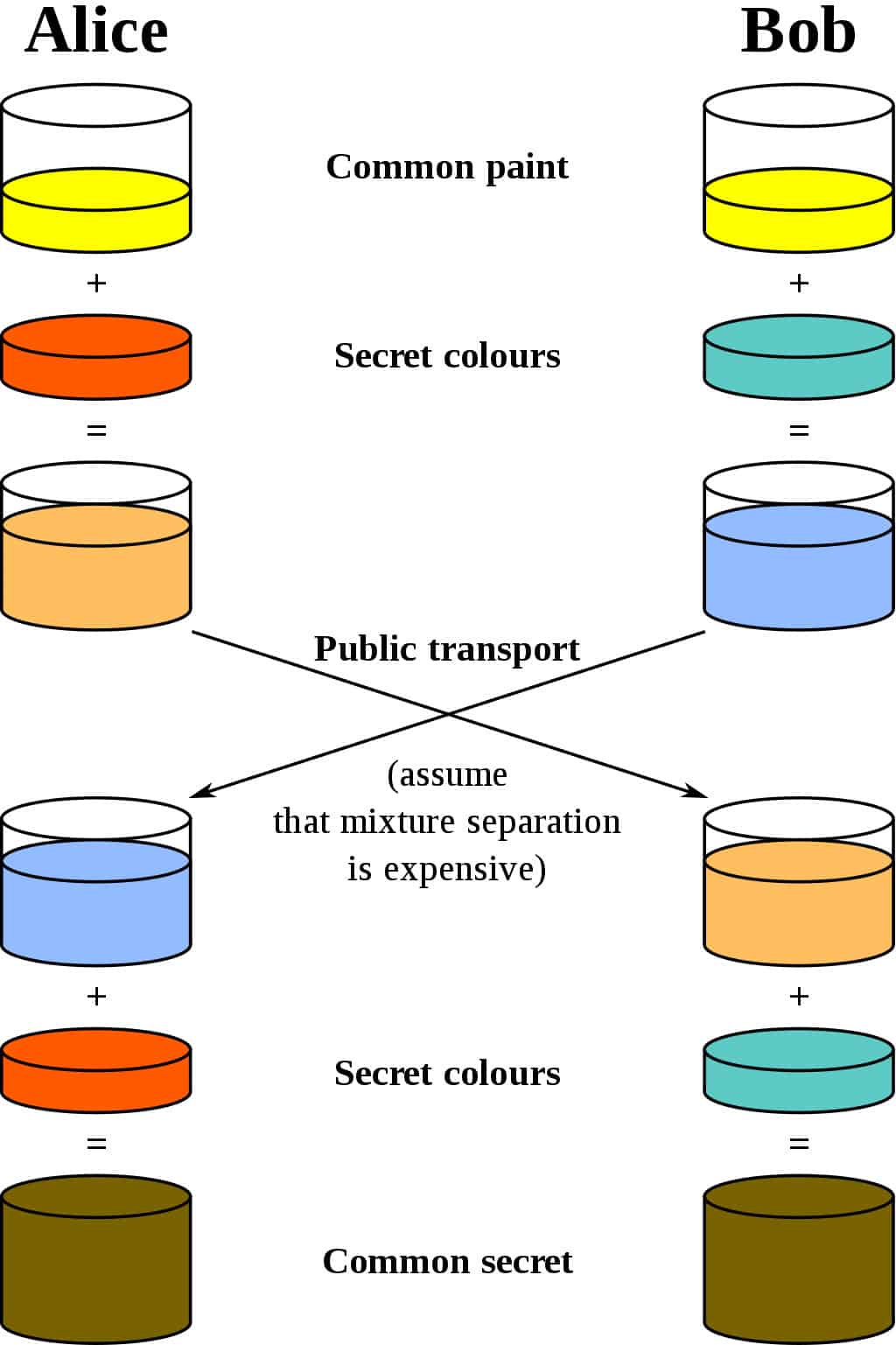
știe propria lor culoare secretă. Ei nu spun celeilalte părți alegerea lor. Să spunem că Alice alege roșu, în timp ce Bob alege a albastru ușor verzui.
Următorul pas este ca Alice și Bob să-și amestece culoarea secretă (roșu pentru Alice, albastru-verzui pentru Bob) cu galbenul pe care au convenit-o reciproc. Conform diagramei, Alice sfârșește cu un amestec de portocale, în timp ce rezultatul lui Bob este un albastru mai profund.
După ce au terminat amestecarea, ei trimit rezultatul celeilalte părți. Alice primește un albastru mai profund, in timp ce Lui Bob i se trimite vopseaua de culoare portocalie.
După ce au primit rezultatul mixt de la partener, își adaugă apoi culoarea secretă. Alice ia albastrul mai adânc și îi adaugă vopseaua roșie secretă, in timp ce Bob adaugă secretul său verde-albastru la amestecul de portocale pe care tocmai l-a primit.
Rezultatul? Amândoi ies cu aceeași culoare, care în acest caz este un maro dezgustător. Este posibil să nu fie genul de culoare cu care doriți să vă vopsiți camera de zi, dar este totuși o culoare împărtășită. Această culoare partajată este denumită ” secret comun.
Partea critică a schimbului de chei Diffie-Hellman este că ambele părți sfârșesc cu același rezultat, fără a fi nevoie să trimită în întregime secretul comun pe canalul de comunicare.. Alegerea unei culori obișnuite, propriile culori secrete, schimbarea mixului și apoi adăugarea propriei culori încă o dată, oferă ambelor părți o modalitate de a ajunge la același secret comun, fără a fi nevoiți niciodată să trimită peste tot.
Dacă un atacator ascultă schimbul, tot ceea ce poate accesa este culoarea galbenă comună cu care încep Alice și Bob, precum și culorile mixte schimbate. Deoarece acest lucru este într-adevăr făcut cu numere enorme în loc de vopsea, aceste informații nu sunt suficiente pentru ca atacul să discerne nici una dintre culorile secrete inițiale, nici secretul comun (din punct de vedere tehnic este posibil să calculăm secretul obținut din aceste informații, dar într-o implementare sigură a schimbului de chei Diffie-Hellman, ar fi nevoie de o cantitate de timp și resurse de calcul imposibile).
Această structură a schimbului de chei Diffie-Hellman este ceea ce o face atât de utilă. Permite celor două părți să comunice printr-o conexiune potențial periculoasă și să vină în continuare cu un secret comun pe care îl pot utiliza pentru a realiza chei de criptare pentru viitoarele lor comunicații. Nu contează dacă ascultă vreun atacator, deoarece secretul complet partajat nu este trimis niciodată prin conexiune.
Detaliile tehnice ale schimbului de chei Diffie-Hellman
Timp pentru ceva matematica …
Nu vă faceți griji, o vom lua lent și vom încerca să facem întregul proces cât mai ușor de înțeles. Urmează o premisă similară cu analogia prezentată mai sus, dar în loc să amestece și să trimită culori, schema Diffie-Hellman face de fapt calcule pe baza numerelor primare excepțional de mari, apoi le trimite pe toate.
Pentru a asigura securitatea, se recomandă ca prim (p) are cel puțin 2048 de biți lungime, care este echivalentul binar al unui număr zecimal de aproximativ această dimensiune:
415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019
Pentru a împiedica capul cuiva să explodeze, vom face această explicație cu un număr mult mai mic. Fiți conștienți de asta schimbul de chei Diffie-Hellman nu ar fi sigur dacă ar folosi numere la fel de mici ca cele din exemplul nostru. Folosim doar un număr atât de mic pentru a demonstra conceptul într-o manieră mai simplă.
În forma cea mai de bază a schimbului de chei Diffie-Hellman, Alice și Bob încep prin a decide reciproc asupra a două numere cu care să înceapă, spre deosebire de vopseaua obișnuită din exemplul de mai sus. Acestea sunt modulul (p) și baza (g).
În utilizare practică, modulul (p) este un număr prim foarte mare, in timp ce baza (g) este relativ mică pentru a simplifica calculele. Baza (g) este derivat dintr-o grupare ciclică (G) care este în mod normal generat cu mult înainte de efectuarea celorlalte etape.
De exemplu, să spunem că modulul (p) este 17, în timp ce baza (g) este 4.
După ce s-au decis reciproc asupra acestor numere, Alice se stabilește pe un număr secret (A) pentru ea însăși, în timp ce Bob alege propriul său număr secret (b). Să spunem că aleg:
a = 3
b = 6
Alice apoi efectuează următorul calcul pentru a-i da numărul pe care îl va trimite lui Bob:
A = ga mod p
În calculul de mai sus, mod semnifică o operație modulo. Acestea sunt, în esență, calcule pentru a descoperi restul după ce a împărțit partea stângă la dreapta. Ca exemplu:
15 mod 4 = 3
Dacă înțelegeți cum funcționează operațiunile modulo, le puteți face singure în următoarele calcule, altfel puteți utiliza un calculator online.
Deci, să punem numerele noastre în formula:
A = 43 mod 17
A = 64 mod 17
A = 13
Când facem același lucru pentru Bob, obținem:
B = 46 mod 17
B = 4096 mod 17
B = 16
Alice îi trimite apoi rezultatul (A) lui Bob, în timp ce Bob își trimite figura (B) către Alice. Alice calculează apoi secretul comun (s) folosind numărul pe care l-a primit de la Bob (B) și numărul ei secret (A), folosind următoarea formulă:
s = Ba mod p
s = 163 mod 17
s = 4.096 mod 17
s = 16
Apoi, Bob efectuează ceea ce este în esență același calcul, dar cu numărul pe care Alice l-a trimis (A), precum și propriul număr secret (b):
s = Ab mod p
s = 136 mod 17
s = 4.826.809 mod 17
s = 16
După cum puteți vedea, ambele părți au încheiat același rezultat pentru s, 16. Acesta este secretul comun, pe care îl cunosc doar Alice și Bob. Ei pot apoi să folosească aceasta pentru a configura o cheie pentru criptarea simetrică, permițându-le să trimită în siguranță informații între ele într-un mod în care numai ei pot accesa.
Rețineți că, deși B și s sunt aceleași în exemplul de mai sus, aceasta este doar o coincidență bazată pe numerele mici care au fost alese pentru această ilustrare. În mod normal, aceste valori nu ar fi aceleași într-o implementare reală a schimbului de chei Diffie-Hellman.
Chiar dacă o mare parte din datele de mai sus sunt trimise pe canal în textul clar (p, g, A și B) și poate fi citit de potențiali atacatori, secretul comun (s) nu se transmite niciodată. Nu ar fi practic ca un atacator să calculeze secretul comun (s) sau oricare dintre numerele secrete (A și b) din informațiile trimise în textul clar.
Desigur, acest lucru presupune că schimbul de chei Diffie-Hellman este implementat corespunzător și sunt utilizate un număr suficient de mare. Atâta timp cât aceste dispoziții sunt respectate, schimbul de chei Diffie-Hellman este considerat un mod sigur de a stabili un secret partajat care poate fi utilizat pentru a asigura comunicațiile viitoare.
Stabilirea unei chei partajate între mai multe părți
Schimbul de chei Diffie-Hellman poate fi, de asemenea, utilizat pentru a configura o cheie partajată cu un număr mai mare de participanți. Acționează în aceeași manieră, cu excepția unor runde suplimentare de calcule necesare pentru fiecare parte să adauge numărul lor secret și să termine cu același secret comun.
La fel ca în versiunea în două părți a schimbului de chei Diffie-Hellman, unele părți ale informațiilor sunt trimise pe canale nesigure, dar nu sunt suficiente pentru ca un atacator să poată calcula secretul comun.
De ce este sigur schimbul de chei Diffie-Hellman?
La nivel matematic, schimbul de chei Diffie-Hellman se bazează pe funcții unidirecționale ca bază pentru securitatea sa. Acestea sunt calcule care sunt simple de făcut într-un singur sens, dar mult mai dificil de calculat invers.
Mai exact, se bazează pe problema Diffie-Hellman, care presupune că în parametrii potriviți, este imposibil să se calculeze gab din valorile separate ale g, gA și gb. În prezent nu există o modalitate cunoscută public de a găsi cu ușurință gab față de celelalte valori, motiv pentru care schimbul de chei Diffie-Hellman este considerat sigur, în ciuda faptului că atacatorii pot intercepta valorile p, g, A, și B.
Autentificare & schimbul de chei Diffie-Hellman
În lumea reală, schimbul de chei Diffie-Hellman este foarte rar folosit de la sine. Motivul principal din spatele acestui lucru este că nu oferă nicio autentificare, ceea ce îi lasă pe utilizatori vulnerabili la atacurile omului în mijloc.
Aceste atacuri pot avea loc atunci când schimbul de chei Diffie-Hellman este implementat de unul singur, deoarece nu are nicio modalitate de a verifica dacă cealaltă parte dintr-o conexiune este cu adevărat cine spune ei. Fără nicio formă de autentificare, utilizatorii se pot conecta de fapt cu atacatorii când cred că comunică cu o parte de încredere.
Din acest motiv, schimbul de chei Diffie-Hellman este în general implementat alături de unele mijloace de autentificare. Acest lucru implică adesea utilizarea certificatelor digitale și a unui algoritm cu cheie publică, precum RSA, pentru a verifica identitatea fiecărei părți.
Variații ale schimbului de chei Diffie-Hellman
Schimbul de chei Diffie-Hellman poate fi implementat în mai multe moduri diferite, oferind, de asemenea, baza pentru alți algoritmi. Unele dintre aceste implementări oferă autorizare, în timp ce altele au diferite caracteristici criptografice, cum ar fi secretul perfect perfect.
Diffie-Hellman curbă eliptică
Curba eliptică Diffie-Hellman profită de structura algebrică a curbelor eliptice pentru a permite implementărilor sale să obțină un nivel similar de securitate cu o dimensiune mai mică a cheii. O cheie curbă eliptică de 224 biți oferă același nivel de securitate ca o cheie RSA de 2048 biți. Acest lucru poate face schimburile mai eficiente și poate reduce cerințele de stocare.
În afară de lungimea mai mică a cheii și de faptul că se bazează pe proprietățile curbelor eliptice, curba eliptică Diffie-Hellman funcționează într-o manieră similară cu schimbul standard de chei Diffie-Hellman.
TLS
TLS, care este un protocol care este utilizat pentru a asigura o mare parte a internetului, poate utiliza schimbul Diffie-Hellman în trei moduri diferite: anonim, static și efemer. În practică, ar trebui implementate doar efemerele Diffie-Hellman, deoarece celelalte opțiuni au probleme de securitate.
- Diffie-Hellman anonim – Această versiune a schimbului de chei Diffie-Hellman nu utilizează nicio autentificare, lăsând-o vulnerabilă la atacurile dintre oameni. Nu trebuie utilizat sau pus în aplicare.
- Static Diffie-Hellman – Static Diffie-Hellman folosește certificate pentru autentificarea serverului. Nu autentifică clientul în mod implicit și nu oferă secret secret.
- Diffie-Hellman efemer – Aceasta este considerată cea mai sigură implementare, deoarece oferă un secret perfect perfect. În general, este combinat cu un algoritm precum DSA sau RSA pentru a autentifica una sau ambele părți din conexiune. Diffie-Hellman efemer utilizează diferite perechi de chei de fiecare dată când este executat protocolul. Aceasta conferă conexiunii secretul perfect perfect, deoarece, chiar dacă o cheie este compromisă pe viitor, nu poate fi folosită pentru a decripta toate mesajele trecute.
ElGamal
ElGamal este un algoritm cu cheie publică construit pe partea de sus a schimbului de chei Diffie-Hellman. Ca și Diffie-Hellman, nu conține nicio prevedere pentru autentificare și, în general, este combinat cu alte mecanisme în acest scop..
ElGamal a fost utilizat în principal în PGP, GNU Privacy Guard și alte sisteme, deoarece principalul său rival, RSA, a fost brevetat. Brevetul RSA a expirat în 2000, ceea ce i-a permis punerea în aplicare liberă după această dată. De atunci, ElGamal nu a fost implementat la fel de des.
STS
Protocolul Station-to-Station (STS) se bazează, de asemenea, pe schimbul de chei Diffie-Hellman. Este o altă schemă de acord-cheie, dar oferă protecție împotriva atacurilor omului în mijloc, precum și secretului perfect perfect..
Este necesar ca ambele părți din conexiune să aibă deja o pauză de cheie, care este folosită pentru autentificarea fiecărei părți. Dacă părțile nu sunt deja cunoscute între ele, atunci certificatele pot fi utilizate pentru a valida identitatea ambelor părți.
Schimbul de chei Diffie-Hellman & RSA
După cum am discutat mai devreme, schimbul de chei Diffie-Hellman este adesea implementat alături de RSA sau de alți algoritmi pentru a oferi autentificare pentru conexiune. Dacă sunteți familiarizat cu RSA, este posibil să vă întrebați de ce oricine s-ar deranja să folosească schimbul de chei Diffie-Hellman, deoarece RSA permite părților care nu s-au întâlnit niciodată să comunice în siguranță.
RSA permite utilizatorilor săi să cripteze mesajele cu cheia publică a corespondentului lor, astfel încât acestea să poată fi decriptate numai cu cheia privată potrivită. Cu toate acestea, în practică, RSA nu este folosită pentru a cripta întreaga comunicare – acest lucru ar fi mult prea ineficient.
În schimb, RSA este adesea folosit doar ca mijloc de autentificare a ambelor părți. Face acest lucru cu certificatele digitale ale fiecărei părți, care vor fi verificate de o autoritate de certificare pentru a demonstra că proprietarul unui certificat este cu adevărat cine spune și că cheia publică a certificatului îi aparține de fapt.
Pentru autentificare reciprocă, fiecare parte va semna un mesaj folosind cheia lor privată și apoi îl va transmite partenerului de comunicare. Fiecare destinatar poate atunci verificați identitatea celeilalte părți verificând mesajele semnate pe cheia publică din certificatul digital al partenerului de comunicare (a se vedea articolul menționat mai sus despre RSA pentru mai multe detalii despre modul în care funcționează, în special pe Semnarea mesajelor secțiune).
După ce ambele părți au fost autentificate, este posibil din punct de vedere tehnic să continue utilizarea RSA pentru a transmite în siguranță mesaje criptate între ele, totuși ar ajunge să fie prea ineficient.
Pentru a evita această ineficiență, multe protocoale de securitate folosesc un algoritm precum schimbul de chei Diffie-Hellman pentru a găsi un secret comun care poate fi utilizat pentru a stabili o cheie simetrică comună. Această cheie simetrică este apoi utilizată într-un algoritm cu cheie simetrică, cum ar fi AES, pentru criptarea datelor că cele două părți intenționează să trimită în siguranță între ele.
Poate părea un proces complex și convolut, dar ajunge să fie mult mai rapid și mai puțin pretențios în ceea ce privește resursele în comparație cu utilizarea unui algoritm cu cheie publică pentru întregul schimb. Asta pentru ca criptarea cu cheie simetrică este o ordine de mărime mai eficientă decât criptarea cu chei publice.
În plus față de ineficiențele pe care tocmai le-am menționat, există și alte dezavantaje care ar rezulta doar din utilizarea RSA. RSA are nevoie de umplutură pentru a-l asigura, astfel încât un algoritm suplimentar ar trebui să fie implementat în mod corespunzător alături de acesta pentru a-l asigura în siguranță.
RSA nu oferă un secret perfect perfect, care este un alt dezavantaj în comparație cu schimbul de chei efemer Diffie-Hellman. În mod colectiv, aceste motive sunt motivele pentru care, în multe situații, este mai bine să aplicați numai RSA împreună cu schimbul de chei Diffie-Hellman.
În mod alternativ, schimbul de chei Diffie-Hellman poate fi combinat cu un algoritm precum Standardul semnăturii digitale (DSS) pentru a oferi autentificare, schimb de chei, confidențialitate și verificarea integrității datelor. Într-o astfel de situație, RSA nu este necesară pentru asigurarea conexiunii.
Probleme de securitate ale schimbului de chei Diffie-Hellman
Securitatea schimbului de chei Diffie-Hellman depinde de modul în care este implementat, precum și de numerele alese pentru acesta. Așa cum am menționat mai sus, nu are nici un mijloc de autentificare a celeilalte părți de la sine, dar în practică sunt folosite alte mecanisme pentru a se asigura că cealaltă parte în legătură nu este un impostor.
Parametri pentru selectarea numărului
Dacă o implementare a lumii reale a schimbului de chei Diffie-Hellman ar folosi numere la fel de mici ca cele din exemplul nostru, ar face banal procesul de schimb pentru ca un atacator să crape. Dar nu este doar dimensiunea numerelor care contează – numerele trebuie să fie suficient de întâmplătoare. Dacă un generator de numere aleatoare produce o ieșire previzibilă, acesta poate submina complet securitatea schimbului de chei Diffie-Hellman.
Numarul p ar trebui să aibă o lungime de 2048 de biți pentru a asigura securitatea. Baza, g, poate fi un număr relativ mic ca 2, dar trebuie să provină dintr-o ordine de G care are un factor prim mare
Atacul Logjam
Schimbul de chei Diffie-Hellman a fost proiectat pe baza problemei discrete de logaritm dificil de rezolvat. Cel mai eficient mecanism cunoscut public pentru găsirea soluției este algoritmul de setare a câmpurilor numerice.
Capacitățile acestui algoritm au fost luate în considerare atunci când a fost proiectat schimbul de chei Diffie-Hellman. Până în 1992, se știa că pentru un grup dat, G, trei din cele patru etape implicate în algoritm ar putea fi calculate în prealabil. Dacă acest progres a fost salvat, etapa finală ar putea fi calculată într-un timp relativ scurt.
Acest lucru nu a fost prea interesant până când nu s-a dat seama că o parte semnificativă a traficului de internet folosește aceleași grupuri cu 1024 biți sau mai mici. În 2015, o echipă academică a efectuat calculele pentru cea mai comună primă valoare de 512 biți folosită de schimbul de chei Diffie-Hellman în TLS.
De asemenea, au putut descărca 80% din serverele TLS care acceptă DHE-EXPORT, pentru a accepta un schimb de chei Diffie-Hellman de 512 biți pentru export pentru conexiune. Aceasta înseamnă că fiecare dintre aceste servere este vulnerabil la atacul unui adversar bine resursat.
Cercetătorii au continuat să-și extrapoleze rezultatele, estimând că un stat-națiune ar putea rupe o primă de 1024 biți. Prin ruperea primului unic cel mai des utilizat de 1024 de biți, echipa academică a estimat că un adversar ar putea monitoriza 18% din un milion de site-uri web cele mai populare HTTPS.
Au continuat să spună că un al doilea prim va permite adversarului să decripteze conexiunile de 66% de servere VPN și 26% de servere SSH. Mai târziu în raport, academicienii au sugerat că ANS ar putea avea deja aceste capacități.
„O lectură atentă a scurgerilor publicate de NSA arată că atacurile agenției asupra VPN-urilor sunt în concordanță cu realizarea unei astfel de pauze.”
În ciuda acestei vulnerabilități, schimbul de chei Diffie-Hellman poate fi în continuare sigur dacă este implementat corect. Atâta timp cât se folosește o cheie de 2048 biți, atacul Logjam nu va funcționa. Browser-urile actualizate sunt, de asemenea, protejate de acest atac.
Este schimbul de chei Diffie-Hellman în siguranță?
În timp ce schimbul de chei Diffie-Hellman poate părea complex, acesta este o parte fundamentală a schimbului sigur de date online. Atâta timp cât este implementat alături de o metodă de autentificare adecvată și numerele au fost selectate corect, nu este considerat vulnerabil la atac.
Schimbul de chei Diffie-Hellman a fost o metodă inovatoare pentru a ajuta două părți necunoscute să comunice în siguranță atunci când a fost dezvoltat în anii ’70. În timp ce acum implementăm versiuni mai noi cu chei mai mari pentru a vă proteja împotriva tehnologiei moderne protocolul în sine pare că va continua să fie sigur până la sosirea calculelor cuantice și atacurile avansate care vor veni cu ea.
Tehnologia de afaceri pentru securitate cibernetică de TheDigitalArtist licențiat sub CC0