Ce este criptarea 3DES și cum funcționează DES?

3DES este un cifru de criptare care a fost derivat din standardul original de criptare a datelor (DES). A devenit proeminent la sfârșitul anilor 90, dar de atunci a căzut în favoarea din cauza creșterii unor algoritmi mai siguri.

Deși va fi învechit în [year], acesta este încă implementat în anumite situații. Întrucât se bazează pe unul dintre primii algoritmi publicat și studiat pe scară largă, DES, este încă important să aflăm despre ce este 3DES și cum funcționează..

Acest ghid vă va parcurge în detaliu fiecare etapă a procesului DES, apoi va descrie modul în care DES este modificat în 3DES pentru a-l face mai sigur. De asemenea, atinge diferitele probleme de securitate și dacă trebuie sau nu să folosiți algoritmul.

Ce este 3DES?

Deși este oficial cunoscut sub numele de algoritmul de criptare a datelor de date (3DEA), cel mai des este denumit 3DES. Acest lucru se datorează faptului că algoritmul 3DES folosește cifrul de date Encryption Standard (DES) de trei ori pentru a cripta datele sale.

DES este un algoritm cu cheie simetrică bazat pe o rețea Feistel. Ca cifru de cheie simetric, folosește aceeași cheie atât pentru procesele de criptare cât și pentru decriptare. Rețeaua Feistel face aceste două procese aproape exact aceleași, ceea ce duce la un algoritm mai eficient de implementat.

DES are atât un bloc pe 64 de biți, cât și o dimensiune a cheii, dar în practică, cheia acordă doar 56 de biți de securitate. 3DES a fost dezvoltat ca o alternativă mai sigură din cauza lungimii mici a cheii DES. În 3DES, algoritmul DES este rulat de trei ori cu trei taste, însă este considerat sigur doar dacă se folosesc trei taste separate.

Utilizările 3DES

Odată ce punctele slabe ale DES normale au devenit mai evidente, 3DES a fost adoptat într-o gamă largă de aplicații. A fost unul dintre schemele de criptare mai des utilizate înainte de creșterea AES.

Unele exemple ale implementărilor sale includ sisteme de plată Microsoft Office, Firefox și EMV. Multe dintre aceste platforme nu mai folosesc 3DES, deoarece există alternative mai bune.

Institutul Național de Standarde și Tehnologie (NIST) a lansat un proiect de propunere care spune că toate formele de 3DES vor fi depășite până în [year] și nu vor fi permise începând cu 2024. Deși este doar un proiect, propunerea semnifică sfârșitul unei ere și a trecut mult timp pentru a trece la alți algoritmi mai siguri..

Istoricul criptării 3DES

Deoarece 3DES este derivat din DES, este mai bine să introducem mai întâi standardul anterior. În anii șaptezeci, Biroul Național de Standarde (BNS – de atunci a fost redenumit NIST) a căutat un algoritm pe care l-ar putea folosi drept standard pentru criptarea informațiilor guvernamentale sensibile, dar neclasificate..

BNS a acceptat propuneri pentru un standard care să se potrivească cerințelor sale, dar niciunul dintre candidații din runda inițială nu a fost adecvat. A invitat mai multe trimiteri, iar de această dată IBM a trimis printr-un algoritm dezvoltat de echipa sa. Trimiterea a fost derivată din cifrul Lucifer pe care Horst Feistel l-a proiectat.

În 1975, algoritmul IBM a fost publicat de BNS ca standard de criptare a datelor propus. Publicul a fost invitat să comenteze designul, ceea ce a atras unele critici.

Criptografi proeminenți, precum Whitfield Diffie și Martin Hellman, designeri ai schimbului de chei Diffie-Hellman, au susținut că lungimea cheii este prea scurtă și că casetele S au fost schimbate de la designul inițial.

La vremea respectivă, mulți din comunitatea criptografică au crezut că NSA a sabotat proiectul și a slăbit algoritmul, astfel că va fi singura agenție care ar putea rupe DES.

Când aceasta a fost investigată de Comitetul de Informații pentru Senat al Senatului Statelor Unite, a constatat că „ANS a convins IBM că o dimensiune redusă a cheilor este suficientă; asistat indirect la dezvoltarea structurilor S-box; și au certificat că algoritmul DES final a fost, în conformitate cu cunoștințele lor, lipsit de orice slăbiciune statistică sau matematică. “

Același raport a continuat să spună că „NSA nu a modificat în niciun fel designul”. Acesta a fost susținut de unii foști personal IBM care au susținut că algoritmul DES a fost conceput în întregime de echipa IBM..

Documentația declasificată a ANS afirmă că agenția „a lucrat îndeaproape cu IBM pentru a consolida algoritmul împotriva tuturor atacurilor cu forțe brute și pentru a întări tabelele de substituție …”

Suspiciunile de modificare a NSA au fost reduse în anii 90, odată ce descoperirea publică a criptanalizei a fost diferențiată. Când s-au testat casetele S mult-maligne cu noua tehnică, s-a găsit că sunt mai rezistente la atac decât dacă ar fi fost alese la întâmplare.

Aceasta indică faptul că echipa IBM știa deja despre criptanaliza diferențială din anii șaptezeci, Steven Levy susținând că NSA le-a cerut să păstreze secretul tehnicii pentru a proteja securitatea națională.

Celebrul criptograf Bruce Schneier a renunțat la o dată, „A fost nevoie de comunitatea academică două decenii pentru a-și da seama că„ modificările ”de la NSA au îmbunătățit de fapt securitatea DES.”

În ciuda întrebărilor inițiale despre securitatea algoritmului și implicarea ANS, algoritmul IBM a continuat să fie aprobat ca Standard Encryption Standard în 1976. A fost publicat în 1977 și reafirmat ca standard în 1983, 1988 și 1993.

Când a fost publicată prima dată criptanaliza în 1994, a început să ridice întrebări despre securitatea algoritmului. În 1997, NIST a anunțat că a căutat un algoritm care să înlocuiască DES. Nevoia unui nou algoritm a fost intensificată pe măsură ce tehnologia se dezvolta în continuare și potențialele atacuri au crescut.

Diverse încercări de fisurare au arătat că este mai puțin dificil să rupi algoritmul decât se credea anterior. În 1998, distribuirea.net a reușit să crape DES este de 39 de zile.

Până la începutul anului 1999, Deep Crack Fundația Electronic Frontier a redus timpul până la puțin peste 22 de ore. Acest lucru a semnalat sfârșitul DES, deoarece un atac de această natură era acum la îndemâna unui adversar cu resurse bune.

Problema principală a fost micul spațiu-cheie și un nou algoritm a fost extrem de necesar. Aceasta a fost o problemă, deoarece NIST ar trebui să se bazeze pe algoritmul care a devenit standardul de înlocuire, Advanced Encryption Standard (AES).

În timp ce s-a decis codul pentru AES, 3DES a fost propus ca o măsură de oprire. Aceasta implică rularea algoritmului DES de trei ori, cu trei taste separate. În 1999, DES a fost reafirmat, dar 3DES este algoritmul ideal. DES normal a fost permis numai în aplicațiile vechi.

3DES a continuat să devină un algoritm de criptare răspândit, deși utilizarea sa grea a resurselor și a limitărilor de securitate au determinat-o să fie înlocuită de AES în majoritatea cazurilor de utilizare..

Înțelegerea algoritmului DES

Înainte de a putea vorbi despre detaliile 3DES, este important să înțelegem algoritmul DES din care este derivat. Deci, să începem chiar de la început.

Folosim criptarea pentru a transforma datele sub formă de text în cifru, care este informație la care nu pot fi accesate atacatorii (atât timp cât utilizăm algoritmi adecvați).

Algoritmii de criptare sunt esențiale formule matematice complexe. Când vine vorba de criptarea ceva de genul „Hai să mergem la plajă”, mulți oameni se confundă. La urma urmei, cum poți aplica matematica pe lucruri precum litere și caractere?

Codificarea textului

Realitatea este că calculatoarele nu se ocupă cu litere și caractere. În schimb, funcționează pe un sistem de 1s și 0 cunoscut sub numele de binar. Fiecare 1 sau 0 este cunoscut ca bit, iar o colecție de opt dintre ele este cunoscută ca un octet.

Puteți să îl căutați manual sau să folosiți un convertor online pentru a vedea că, în mod binar, „Hai să mergem la plajă” devine:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111 00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000 01100010 01100101 01100001 01100011 01101000

blocuri

Când datele sunt criptate, acestea sunt împărțite în blocuri separate pentru procesare. DES are o dimensiune a blocului pe 64 de biți, ceea ce înseamnă că, în esență, fiecare bloc se potrivește unui mix de 64 de altele și zerouri. Primul nostru bloc (primele 64 de cifre ale binarului prezentat mai sus) ar fi:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Al doilea nostru ar fi:

00100000 01110100 01101111 00100000 01110100 01101000 01100101 00100000

Iar blocul nostru final ar fi:

01100010 01100101 01100001 01100011 01101000

umplutură

Este posibil să fi observat că al treilea bloc al nostru are doar 40 de biți. Înainte de a putea fi criptat, trebuie să fie construit până la o dimensiune de bloc pe 64 de biți. Acest lucru se face cu umplutură, care implică adăugarea de informații suplimentare la un bloc pentru a o completa. Acest lucru se poate face cu o serie de scheme diferite și, de asemenea, poate servi pentru a face informațiile criptate mai greu de fisurat, dar nu vom intra în asta în acest articol.

Programul cheii DES

Algoritmii de criptare utilizează chei pentru a adăuga date care vor modifica rezultatul final al procesului. Dacă DES a implicat doar pași precum permutarea și casetele S (permutarea este explicată mai jos, în timp ce casetele S sunt acoperite în Substituţie secțiunea), tot ce ar trebui să facă un atacator este să descopere detaliile algoritmului, apoi să efectuați fiecare dintre pașii invers pentru a dezvălui mesajul inițial.

Deoarece majoritatea algoritmilor noștri sunt cunoscuți pe scară largă, acest lucru nu ar adăuga foarte multă securitate. În schimb, tastele secrete sunt adăugate pentru a modifica ieșirea într-un mod care nu poate fi prevăzut doar prin cunoașterea algoritmului (atât timp cât se folosește un algoritm suficient de complex).

DES începe cu o singură cheie, care este folosită pentru a face sub-chei care sunt aplicate în fiecare rundă. Aceasta este o cheie pe 64 de biți, care are aceeași dimensiune ca blocurile noastre. Să spunem că cheia noastră este:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

Acum, este cheie în modul binar, care este modul în care datele sunt exprimate atunci când computerele le procesează. Când oamenii se ocupă de chei, vor apărea în mod normal ca un amestec de caractere, ceva de genul:

kj329nf982bc9wn1

În DES, primul pas în derivarea tastelor noastre rotunde este să permită cheia (să o mutați) în conformitate cu următorul tabel:

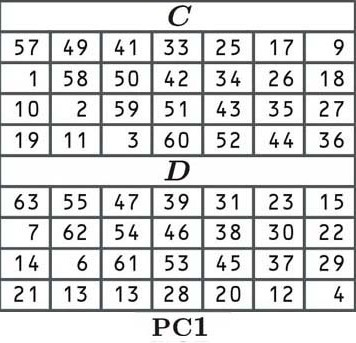
La permutare, fiecare biț din cheia noastră originală este mutat într-o poziție nouă, așa cum este indicat de tabel. Deoarece spune celula din colțul din stânga sus (al lui C) 57, primul număr al cheii noastre permise va fi numărul din poziția a 57-a a blocului nostru vechi:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 11111010

A doua celulă spune 49, ceea ce înseamnă că a doua cifră a noii noastre chei va fi numărul care se află în a 49-a poziție a blocului nostru vechi:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

Cea de-a treia celulă spune 41, deci căutăm cifra la a 41-a poziție:

01001010 10101101 11101000 10100101 01110001 01010100 10101001 1111010

Până în prezent, cheia noastră este alcătuită din „110“.

Restul cheii este aranjat în același mod, în funcție de valorile tabelului. Ne deplasăm de la stânga la dreapta și, după ce ajungem la capătul unui rând, sărim la următorul, la fel de normal. O singura data tabelul C este terminat, sărim la tabelul D pentru a finaliza a doua jumătate a cheii.

Nu există nicio modalitate ușoară de a transpune întregul bloc în conformitate cu tabelul de permutare inițială. Ați putea face totul manual sau puteți scrie un scenariu pentru acesta (sau chiar aveți noroc și găsiți unul în profunzimea internetului), dar vom înșela și vom alcătui:

1100010 1010010 1010101 0101010 1010000 1111001 0001011 1000111

S-ar putea să vă faceți griji că alcătuim unele dintre numerele din acest ghid, dar realitatea este că nu contează cu adevărat. Nimeni nu mai criptează datele manual, totul se face prin programe. Cel mai critic aspect al acestui tutorial este acela că aveți o idee clară a conceptelor cu care avem de-a face. Numerele în sine servesc doar pentru a vă ajuta să vizualizați ce se întâmplă.

Este posibil ca unii cititori să fi observat că tabelul (și acum cheia noastră), are doar 56 de biți mai degrabă decât 64. Acest lucru se datorează faptului că fiecare al optulea bit este omis. Acesta este un artefact din zilele anterioare ale tehnologiei, când a fost important să existe biți de verificare a parității, care au verificat dacă cheia a fost primită corect. Aceste biți de verificare a parității înseamnă că, în practică, DES are doar securitatea unei chei de 56 de biți.

Tabelele C și D ne oferă o cheie care are două jumătăți de 28 de biți. Uneori, jumătățile sunt denumite C și D, dar în tot acest articol ne vom referi la ele ca L și R, pentru stânga și dreapta. Partea noastră stângă este:

1100010 1010010 1010101 0101010

În timp ce dreptul nostru este:

1010000 1111001 0001011 1000111

Următorul pas este mutarea cheii cu unul sau două spații spre stânga, în funcție de runda. Numărul exact de spații este decis în funcție de următorul tabel predeterminat:

Numărul rotund Număr de schimburi stângi

1	1
2	1
3	2
4	2
5	2
6	2
7	2
8	2
9	1
10	2
11	2
12	2
13	2
14	2
15	2
16	1

Deci, să ne luăm jumătățile din stânga și din dreapta:

L 1010010 1010010 1010101 0101010

R 1010000 1111001 0001011 1000111

Și deplasați amândouă o poziție spre stânga, deoarece primul tur are o schimbare de 1 conform tabelului (numărul de la capătul din stânga este mutat la capătul drept).

Subcheia din prima rundă:

L 0100101 0100101 0101010 1010101

R 0100001 1110010 0010111 0001111

În a doua rundă, tabelul mai spune 1, deci acest rezultat va fi din nou modificat mutând fiecare poziție numărul unu spre stânga.

Runda a doua subcheie:

L 1001010 1001010 1010101 0101010

R 1000011 1100100 0101110 0011110

În a treia rundă, numerele vor fi mutate în două locuri spre stânga, deoarece tabelul spune acum 2.

Subcheia a treia rundă:

L 0101010 0101010 1010101 0101010

R 0001111 0010001 0111000 1111010

În rundele ulterioare, numerele sunt mutate la stânga în funcție de distanțele specificate în tabel, fiecare schimbare fiind aplicată la rezultatul rundei anterioare. În cele din urmă, aceasta ne oferă șaisprezece sub-cheie diferite, una pentru fiecare rundă a procesului DES.

Următorul pas este o altă permutare conform tabelului PC2 prezentat mai jos:

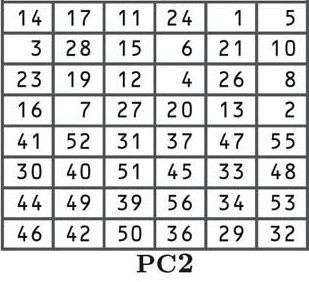
Până acum, ar trebui să fiți familiarizați cu permutațiile, deci nu vom intra în proces în profunzime. Dacă doriți să vedeți cum funcționează mai detaliat, consultați explicația de lângă începutul acestei secțiuni. Deși pozițiile de relocare sunt diferite, procesul este același.

Fiecare din cele 16 taste derivate în procesul de schimbare sunt acum amestecate conform tabelului, numărul din poziția a 14-a a fost mutat pe primul loc, al 17-lea la al doilea, al 11-lea până la al treilea, etc…

Dacă te uiți atent la tabel, vei observa că există doar 48 de biți, mai degrabă decât cele 56 de biți pe care le-am avut anterior. Acest proces este cunoscut sub numele de permutarea compresiei.

Puteți vedea, de asemenea, că jumătatea superioară a tabelului conține numere între unu și 28, în timp ce jumătatea de jos conține numere de la 29 la 56. Aceasta menține separat jumătatea din stânga și cea dreaptă a subtech-urilor noastre și este indicată mai jos de spațiul mai mare în mijlocul tastelor.

Din nou, vom înșela și vom alcătui numerele. Să spunem că acest întreg proces ne-a oferit următoarele sub-cheie:

Runda unu:         010101 010101 101010 110100 101001 100101 101010 101010

Runda doi:         011010 110101 101110 110010 010100 110010 111101 101101

Runda a treia:     010100 100110 110110 101010 100110 011000 101011 011001

Runda a patra:         011001 110101 011001 110101 000011 001011 010101 010101

Runda cinci:         110101 001101 010101 010101 010011 001011 010111 100101

Runda a șasea:           010111 110101 011001 111001 101001 100101 101010 101010

Runda șapte:     110101 111010 101110 101010 100110 010110 111011 001110

Runda opt:       011001 110101 010101 001001 010011 001011 010100 101010

Runda nouă:         111011 011010 011110 100010 100010 010110 110011 110010

Runda 10:             011010 010101 101110 101001 010010 010110 111000 101010

Runda 11:             110101 001101 101110 101010 100101 100101 101010 001010

Runda 12:             101001 100100 101001 101010 100110 011000 101011 011001

Runda 13:             010010 010010 010101 010101 010110 110001 100101 101010

Runda 14:             101001 100110 010101 011101 010001 001010 110010 111110

Runda 15:             011001 011010 011001 110101 001001 011001 100101 101101

Runda 16:             010010 100110 010101 010101 010001 101000 110010 111010    

Acest proces de schimbare duce la fiecare bit din cheia inițială fiind utilizat în aproximativ 14 din cele 16 sub-chei, deși unele biți sunt utilizate puțin mai mult decât altele.

Permutarea inițială

După ce datele au fost împărțite în blocuri și completate dacă este necesar, este timpul să începeți procesul de criptare DES. Vom reveni la subkey-urile pe care tocmai le-am creat într-o etapă ulterioară. Primul pas este cunoscut sub numele de permutarea inițială, unde datele sunt rearanjate conform tabelului următor:

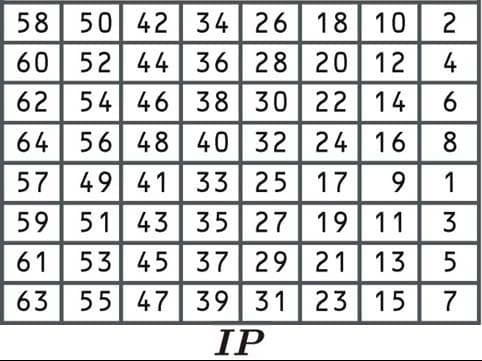
Acest proces de permutare inițială nu face algoritmul mai sigur. Acest lucru se datorează faptului că nu implică introducerea niciunei chei și poate fi inversat cu ușurință. Algoritmul a fost inițial conceput astfel, deoarece a făcut implementarea mai ușoară în anumite contexte.

Deoarece am acoperit permutările de câteva ori, vom omite orice explicație majoră aici. Capul înapoi la Programul cheii DES secțiune dacă aveți nevoie de mai multe informații despre modul în care funcționează.

Să luăm primul bloc din mesajul „Hai să mergem la plajă”, pe care l-am derivat în bloc secțiune sub Înțelegerea algoritmului DES:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

De când spune prima celulă 58, am selecta numărul din poziția a 58-a:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Apoi vom lua numărul de pe poziția 50:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Și numărul de la a 42-a poziție:

01001100 01100101 01110100 00100111 01110011 00100000 01100111 01101111

Acest lucru ne oferă „110” pana acum. Vom alcătui restul numărului:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Când permutarea inițială este completă, datele sunt trecute la pasul următor.

Împărțirea blocurilor

Odată ce datele au suferit permutarea inițială, acestea sunt împărțite în două jumătăți. Luăm blocul nostru care tocmai a suferit permutarea sa inițială:

11010111 01001010 10101000 10011101 01001011 10110101 10000111 10101001

Și îl vom separa în două blocuri, un bloc din stânga (format din primele 32 de cifre), cunoscut ca L0:

L0    11010111 01001010 10101000 10011101

Și un bloc drept (format din a doua 32 de cifre), cunoscut sub numele de R0:

R0    01001011 10110101 10000111 10101001

Funcția F

După ce blocul a fost împărțit, a venit timpul pentru funcția F. În prima rundă, acesta va fi aplicat doar pe jumătatea dreaptă a blocului, în timp ce jumătatea stângă este păstrată deoparte până mai târziu. Partea dreaptă parcurge următoarele patru etape ca parte a funcției F:

• Permutarea extinderii (E în diagramă)
• Amestecarea tastelor (⊕ în diagramă)
• Înlocuire (fiecare S1, S2 etc. în diagramă)
• Permutarea (P în diagramă)

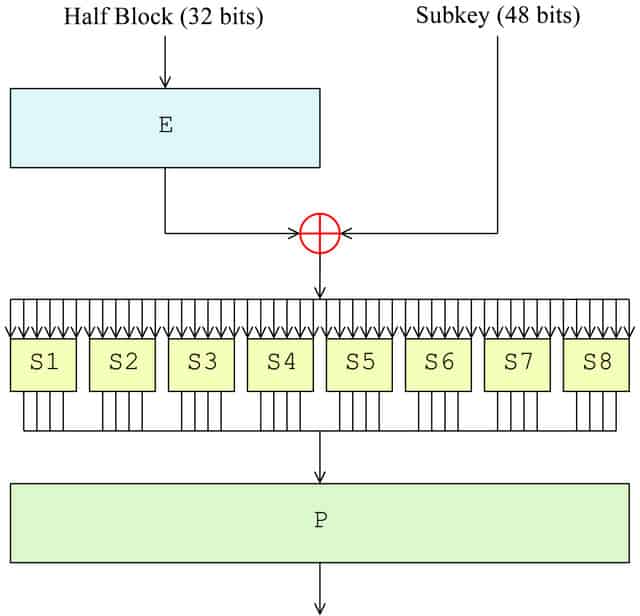
Permutarea extinderii

Permutarea de expansiune realizează trei lucruri. Cel mai important este faptul că permite unui singur bit de date de intrare să afecteze ieșirea altor doi biți, provocând un efect de avalanșă. De asemenea, face jumătatea potrivită de 48 de biți, astfel încât să aibă aceeași dimensiune ca subcheia pentru pasul următor. Celălalt efect al permutării de expansiune este acela că face ieșirea mai lungă decât intrarea. Acest lucru îi permite comprimarea în operația de înlocuire.

Biții sunt rearanjați conform tabelului următor. Unele dintre biții individuali sunt în tabel de două ori, care este modul în care blocul s-a extins de la 32 la 48 de biți:

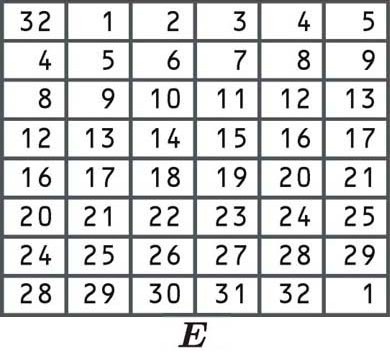
Deoarece prima celulă spune 32, ne luăm blocul din dreapta și selectăm numărul din poziția a 32-a, la fel cum am făcut și în celelalte exemple de permutare enumerate mai sus:

R0    01001011 10110101 10000111 10101001

Luăm apoi numerele din prima poziție, a doua poziție și așa mai departe, chiar în sus, până ajungem în colțul din dreapta jos al blocului. Deoarece există un 1 în această celulă, ultima cifră va fi și numărul care apare în prima poziție a blocului nostru.

Să presupunem că permutarea de expansiune ne oferă un nou bloc de 48 de biți din:

101110 100110 100100 000000 001100 001110 101101 011110

Mixarea tastelor

După ce blocul a fost extins la 48 de biți, este timpul să aplicăm subcheia primei runde, pe care am derivat în Program cheie DES secțiunea de mai sus. Blocul este modificat de sub-cheie folosind cifrul XOR.

Criptarea XOR este o cifră adițională care urmează un proces simplu, mai ales în comparație cu celelalte elemente despre care am discutat deja.

Într-un cript XOR:

0 + 0 = 0

1 + 0 = 1

1 + 1 = 0

Deci, să zicem că trebuie să XOR următoarele două numere în binar:

1101

0101

Fiecare cifră ar fi adăugată la cea de dedesubt. Conform celor trei reguli prezentate mai sus, acest lucru dă un rezultat de:

1000

Pentru a finaliza pasul de amestecare a tastelor, luăm partea dreaptă a blocului nostru pe care tocmai l-am extins la 48 de biți și cheia din prima rundă. Apoi efectuăm adăugarea XOR:

Bloc:                      101110 100110 100100 000000 001100 001110 101101 011110

Cheia rotundă:     010101 010101 101010 110100 101001 100101 101010 101010

Rezultat XOR:             111011 110011 001110 110100 100101 101011 000111 110100

Rezultatul operației XOR este trecut apoi la runda următoare.

Substituţie

Înlocuirea adaugă confuzie la date. În mod normal se face cu tabele de căutare, care sunt, de asemenea, cunoscute sub numele de casete de substituție sau S-casete. DES folosește opt tabele sau cutii S separate, una diferită pentru fiecare 6 biți de date. Următorul tabel prezintă cele opt casete S ale DES:

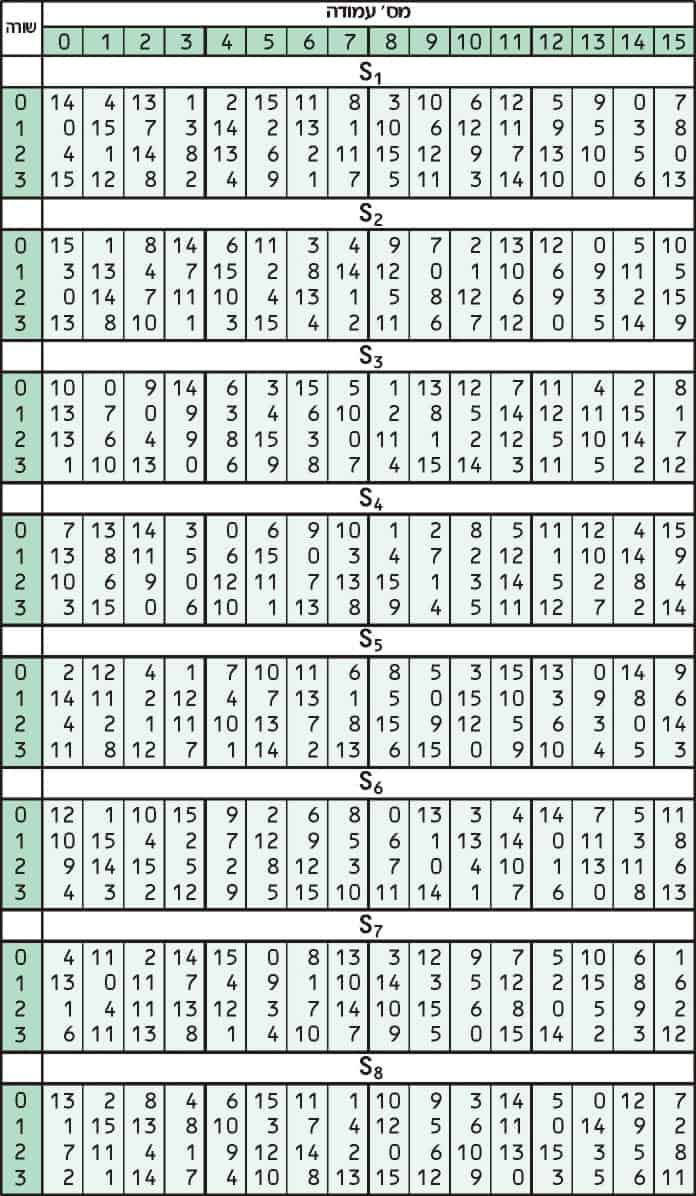
Cele opt cutii S separate sunt folosite pentru a transpune fiecare intrare de 6 biți într-o ieșire pe 4 biți. Primul pas în proces este să luați cifrele la începutul și sfârșitul unui segment de 6 biți, apoi să convertiți acea valoare binară în zecimale.

Să luăm datele pe care tocmai le-am terminat XORing în pasul anterior:

111011 110011 001110 110100 100101 101011 000111 110100

Vom analiza primul segment pe 6 biți pentru a vă arăta cum funcționează procesul de substituție:

111011

Deoarece primul număr și ultimul număr sunt ambele 1, acest lucru ne oferă o valoare de 11. Ne convertim apoi 11 de la binar la zecimal, ceea ce ne dă 3. Acestea sunt doar valori echivalente, scrise în moduri diferite. Gândiți-vă la el ca la conversia limbajului computerului în limbaj uman. Puteți verifica conversia pentru dvs. cu un calculator online dacă doriți.

Luăm apoi cele patru cifre medii ale primului segment de 6 biți:

111011

Și convertiți-le de la binar la zecimal. 1101 se traduce la numărul 13.

Acum, luăm aceste două numere și le privim în secțiunea S1 masa:

               

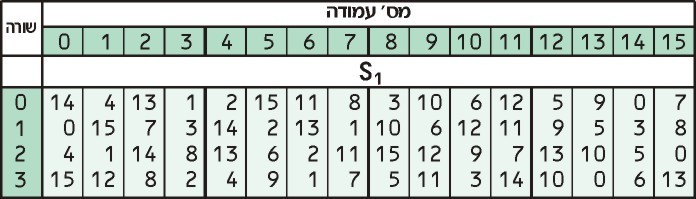
Primul nostru număr, 3, ne spune să privim în al treilea rând, în timp ce al doilea număr, 13 ne spune să ne uităm în coloana a 13-a. Valoarea din cel de-al treilea rând al celei de-a 13-a coloane este 0.

Acum că am căutat numărul nostru în tabel, îl convertim înapoi în două cifre binare. În mod normal, zero este scris ca 0 în mod binar, dar 0000 este același și acesta este formatul cel mai potrivit pentru scopurile noastre.

În urma acestui proces, caseta S transformă prima noastră secțiune de date pe 6 biți (111011) într-o valoare diferită de 4 biți (0000). Pare convolut, dar această tehnică ajută la întunecarea în continuare a relației dintre cifră de text și textul clar la care este legată.

Următoarea secțiune de 6 biți de date trece apoi prin același proces, dar în schimb utilizează caseta S2 prezentată mai sus. A treia secțiune folosește tabelul S3 și așa mai departe, până când secțiunea finală suferă înlocuirea prin tabelul S8.

Din nou, vom înșela pentru restul valorilor. Să zicem că casetele de substituție ne oferă un rezultat din:

0000 1010 1100 1001 0100 1001 0111 0001

Odată ce fiecare secțiune a datelor a trecut prin caseta sa S, aceasta trece la pasul următor.

Permutare

Ultima etapă a funcției F este o altă permutare, folosind următorul tabel: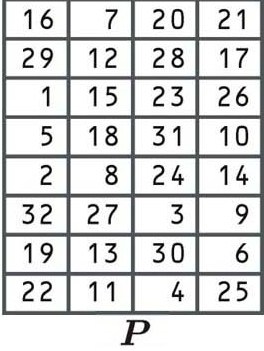

Până acum, ar trebui să înțelegeți în mod decent modul în care permutațiile mută cifrele din blocul vechi într-o poziție diferită în noul bloc, deci nu vom mai intra în el.

Să spunem că această permutare are rezultatul nostru anterior:

0000 1010 1100 1001 0100 1001 0111 0001

Și ne oferă o ieșire din:

0101 0110 1001 0101 0010 0100 0101 0010

Acum că s-a finalizat permutarea, am terminat cu cei patru pași ai funcției F din această rundă. În notație matematică, această valoare este cunoscută sub numele de f (R0, K1). Aceasta înseamnă că rezultatul este funcția (f) din partea dreaptă inițială a blocului (R0) și subcheia primei runde (K1).

XOR cu blocul din stânga

Vă amintiți cum împărțim blocul în jumătate chiar înainte de a începe pașii funcției F? Am pus deoparte partea stângă a blocului (L0), în timp ce partea dreaptă a suferit fiecare din aceste procese. Ei bine, acum este timpul ca L0 să revină în acțiune.

Luăm partea dreaptă pe care tocmai am procesat-o f (R0, K1) și adăugați-o în partea stângă veche (L0) folosind cifrul XOR. Acest lucru ne dă R1, rezultatul primei noastre runde:

f (R0, K1):                         0101 0110 1001 0101 0010 0100 0101 0010

L0:                                    1101 0111 0100 1010 1010 1000 1001 1101

Rezultat XOR (R1):              1000 0001 1101 1111 1000 1100 1100 1111

Consultați secțiunea Mixarea tastelor secțiunea de mai sus dacă aveți nevoie de un memento despre cum funcționează cifrarea XOR.

Încă 15 runde …

Dacă ați ajuns până acum, atunci DES pare probabil un proces dificil. Dar nici măcar nu este aproape să fie terminat. Datele parcurg cele patru etape ale funcției F, urmate de XOR, încă de 15 ori, pentru un total de 16 runde.

În a doua rundă, luăm versiunea originală, neatinsă, din partea dreaptă a blocului (R0) și facem din nou partea stângă (L1). Între timp, luăm rezultatul primei noastre runde și îl trimitem prin funcția F. Totul se întâmplă la fel ca data trecută, însă de data aceasta se folosește sub-cheia pentru a doua rundă. Să spunem că acest proces ne oferă un rezultat din:

f (R1, K2):        1011 0111 1000 1011 1001 1101 1001 1110

Atunci XOR rezultatul este cu L1, care este de fapt R0 (am derivat acest lucru în Împărțirea blocurilor secțiune). Acest lucru ne oferă rezultatul celei de-a doua runde, R2:

f (R1, K2):           1011 0111 1000 1011 1001 1101 1001 1110

L1:                      0100 1011 1011 0101 1000 0111 1010 1001

R2:                     1111 1100 0011 1110 0001 1010 0011 0111

Acest pas poate părea un pic confuz, dar în schema Feistel, partea dreaptă veche devine noua stânga, în timp ce rezultatul operației devine noua parte dreaptă.

Următoarea diagramă vă oferă o reprezentare vizuală a ceea ce se întâmplă. IP reprezintă permutația inițială, F este un stand-in pentru întreaga funcție F, ⊕ simbolizează funcția XOR, iar săgețile indică fiecare parte a blocului care se mișcă între stânga și dreapta:

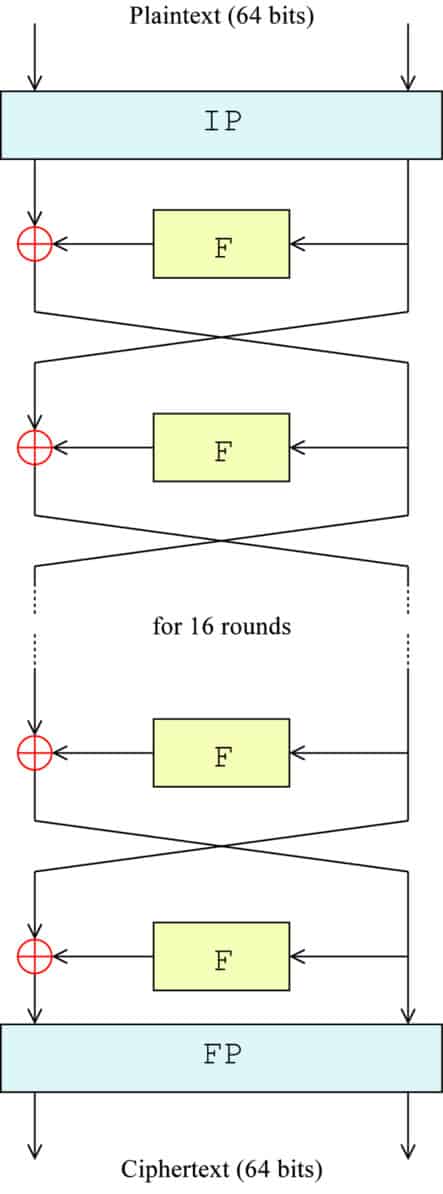
Formula exactă pentru fiecare pas este:

Ln = Rn-1

Rn = Ln-1 + f(Rn-1,Kn)

Unde:

L = jumătatea stângă a blocului (începând cu L0 când blocul a fost inițial împărțit)

R = jumătatea dreaptă a blocului (începând cu R0 când blocul a fost inițial împărțit)

n = Numărul rotund (începând cu 0, când blocul a fost inițial împărțit)

f = Funcția F

Kn = Subcheia pentru runda n

Conform formulei și diagramei, în a treia rundă, R1 devine jumătatea nouă stângă (L2), în timp ce R2 este procesată prin funcția F. Să spunem că ne oferă un rezultat din:

f (R2, K3)        1001 0111 0000 1011 1101 0111 1011 1011

Apoi calculăm rezultatul celei de-a treia runde (R3), folosind cifrul XOR, la fel ca înainte:

f (R2, K3):           1011 0111 1000 1011 1001 1101 1001 1110

L2:                      0100 1011 1011 0101 1000 0111 1010 1001

R3:                      1111 1100 0011 1110 0001 1010 0011 0111

Același proces continuă până la a cincisprezecea rundă, blocurile comutând și următoarea sub-cheie fiind folosită în fiecare rundă. În a 16-a și ultima rundă, blocurile nu sunt schimbate. În schimb, acestea sunt combinate pentru a forma un bloc pe 64 de biți. Abținerea de la schimbarea blocurilor în această ultimă etapă permite utilizarea algoritmului atât pentru criptare cât și pentru decriptare.

Să spunem că runda finală ne oferă un rezultat din:

1010 0101 0100 1011 1001 0001 0100 1000 0101 1010 1101 0001 1101 1001 1001 1101

Permutarea finală

Această permutare este inversă permutării inițiale și, din nou, nu adaugă o valoare suplimentară de securitate. Reorganizează datele în conformitate cu următorul tabel:

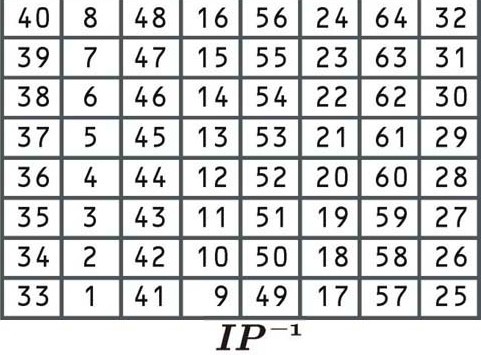
Acest tabel de permutare funcționează la fel ca cele anterioare. Deoarece este ultimul pas al procesului de criptare, rezultatul va fi cifra pentru primul bloc din „Sa mergem la plajă”. Să spunem că blocul criptat este:

0100 1001 0011 0010 1001 0101 0111 0100 1011 1010 0111 0101 0111 1010 0101 0101

Acum, dacă ai fi dorit adevăratul cifru pentru „Să mergem la plajă”, ai fi putut sări peste întregul proces de învățare și să te duci direct la un instrument online de criptare DES. Dacă introducem propoziția alături de o cheie (să zicem kj329nf982bc9wn1), instrumentul ne oferă un text criptat din:

U2FsdGVkX19Pienyu3w3q4zCd2IPKEPUWBzu3AeyVu2H3FeimZe6hA

Dacă doriți, puteți transforma cheia și cifrul textului în mod binar și apoi puteți compara modul în care cifra de text a primului bloc se aliniază întregului proces care a fost conturat.

DESCriptare DES

În DES, procesul de decriptare este incredibil de simplu. Structura algoritmului Feistel îi permite să fie inversat cu ușurință. Procesul este rulat aproape exact la fel pentru a decripta informația. Singura diferență este că sub-tastele sunt aplicate invers. Aceasta este o configurare eficientă, deoarece înseamnă că același software și hardware pot fi utilizate atât în ​​procesele de criptare cât și de decriptare..

Pentru a decripta datele, mai întâi trece printr-o permutare inițială, apoi blocul este împărțit și jumătatea dreaptă trece prin funcția F. Diferența este că în prima rundă de decriptare, se aplică cea de-a 16-a sub-cheie. Orice altceva decurge la fel de normal. Odată ce funcția F este finalizată, este XORed cu partea stângă a blocului.

Blocurile sunt comutate și rezultatul parcurge același proces pentru a doua rundă, cu singura excepție că se aplică cea de-a 15-a sub-cheie. Acest proces continuă până la etapa a 16-a, când se folosește prima sub-cheie.

La fel ca în procesul de criptare, blocurile nu sunt schimbate în etapa finală, iar datele sunt supuse unei permutări finale. Aceasta finalizează procesul de decriptare, rezultând textul original al mesajului.

3DES

Pe măsură ce slăbiciunile de securitate ale DES au devenit mai evidente, 3DES a fost propus ca o modalitate de extindere a dimensiunii cheii sale fără a fi nevoie să construiți un algoritm complet nou. În loc să folosească o singură cheie ca în DES, 3DES rulează algoritmul DES de trei ori, cu trei taste de 56 de biți:

• Cheia unu este folosit pentru a criptați textul complet.
• Cheia a doua este obișnuită Decriptare textul care fusese criptat de cheia unu.
• Se folosește cheia trei criptați textul care a fost decriptat de cheia a treia.

În fiecare etapă, procesul complet DES este urmat așa cum este prezentat mai sus.

Acum, este posibil să vă întrebați „Cum puteți aplica decriptarea în a doua etapă pentru a îmbunătăți securitatea?”

Răspunsul este că folosește o cheie separată. Dacă prima cheie a fost folosită și pentru a decripta datele în a doua etapă, atunci datele ar fi înapoi chiar de unde au început.

Cu toate acestea, din moment ce utilizează o altă cheie, procesul de decriptare nu servește de fapt la decriptarea datelor. Poate părea logic pervers, dar decriptarea cu o cheie separată nu face decât să mărească datele și mai departe.

Odată ce a doua cheie a „decriptat” datele, a treia cheie este aplicată pentru a o cripta din nou. Rezultatul este textul 3DES.

3DES este structurat în acest fel, deoarece permite implementarea să fie compatibilă cu o cheie unică DES, două chei DES și trei chei DES (acestea sunt incluse în secțiunea următoare). Acest lucru nu ar funcționa dacă s-ar utiliza criptarea în toate cele trei etape.

Opțiuni de tastare 3DES

Tehnic, 3DES poate fi implementat cu trei configurații cheie diferite. În ciuda acestui fapt, a doua și a treia opțiune sunt nesigure și nu ar trebui implementate niciodată.

• Tastați opțiunea 1 – Această opțiune folosește trei taste independente și este cea mai sigură.
• Completarea opțiunii două – În această configurație, primele și a treia taste sunt aceleași.
• Tastați opțiunea trei – Aceasta folosește trei taste identice. Când se utilizează chei identice, procesul de decriptare din a doua etapă anulează prima criptare, lăsând doar criptarea finală să modifice datele. Acest lucru face ca rezultatul să fie la fel ca DES obișnuit.

Procesul 3DES: prima opțiune de strângere

Să fim sinceri, întregul proces 3DES vă poate face să se învârtă capul, mai ales dacă sunteți nou la criptografie. Pentru a-l ajuta să se afunde, iată un scurt rezumat al întregii scheme de criptare a algoritmului 3DES:

Textul integral intră în algoritmul 3DES și este pe primul loc criptat cu tasta 1 în următorii pași:

• • Program cheie – cele 16 sub-chei sunt derivate din prima cheie

  • Permutarea inițială

  • Blocul este împărțit în jumătate stânga și dreapta

• • • Jumătatea dreaptă este trimisă prin funcția F

      • Permutarea extinderii

      • XOR cu sub-cheia pentru rundă

      • Substituţie

      • Permutare

    • XOR rezultatul funcției F cu partea stângă

    • Faceți partea dreaptă veche pe partea nouă stângă, iar rezultatul este partea nouă dreapta

      Repetați pașii de mai sus de 14 ori

• • • Jumătatea dreaptă este trimisă prin funcția F

      • Permutarea extinderii

      • XOR cu subcheia pentru etapa a 16-a

      • Substituţie

      • Permutare

    • XOR rezultatul funcției F cu partea stângă

    • Combinați partea stângă și dreapta a blocului

• • Permutarea finală

Luați textul care a fost criptat cu o cheie, apoi trimiteți-l prin Proces de „decriptare” cu cheie Două:

• • Program cheie – cele 16 sub-chei sunt derivate din două cheie

  • Permutarea inițială

  • Blocul este împărțit în jumătate stânga și dreapta

• • • Jumătatea dreaptă este trimisă prin funcția F

      • Permutarea extinderii

      • XOR cu sub-cheia pentru rundă (începând cu a 16-a sub-cheie pentru decriptare)

      • Substituţie

      • Permutare

    • XOR rezultatul funcției F cu partea stângă

    • Faceți partea dreaptă veche pe partea nouă stângă, iar rezultatul este partea nouă dreapta

      Repetați pașii de mai sus de 14 ori

• • • Jumătatea dreaptă este trimisă prin funcția F

      • Permutarea extinderii

      • XOR cu subcheia pentru prima rundă

      • Substituţie

      • Permutare

    • XOR rezultatul funcției F cu partea stângă

    • Combinați partea stângă și dreapta a blocului
  • Permutarea finală

Luați datele care au fost „decriptate” de cheia a doua, apoi trimiteți-o prin intermediul roproces de criptare cu cheie Trei:

• • Program cheie – cele 16 sub-chei sunt derivate din cele trei chei

  • Permutarea inițială

  • Blocul este împărțit în jumătate stânga și dreapta

• • • Jumătatea dreaptă este trimisă prin funcția F

      • Permutarea extinderii

      • XOR cu sub-cheia pentru rundă

      • Substituţie

      • Permutare

    • XOR rezultatul funcției F cu partea stângă

    • Faceți partea dreaptă veche pe partea nouă stângă, iar rezultatul este partea nouă dreapta

      Repetați pașii de mai sus de 14 ori

• • • Jumătatea dreaptă este trimisă prin funcția F

      • Permutarea extinderii

      • XOR cu subcheia pentru etapa a 16-a

      • Substituţie

      • Permutare

    • XOR rezultatul funcției F cu partea stângă

    • Combinați partea stângă și dreapta a blocului

• • Permutarea finală

Rezultatul este textul 3DES.

Securitatea 3DES

Securitatea 3DES depinde de ce opțiune de taste este folosită. Opțiunea de introducere a tastei implică trei taste diferite de 56 de biți, ceea ce îi oferă o lungime totală a tastei de 168 de biți. Lungimea efectivă este redusă considerabil prin atacuri de întâlnire în mijloc, care reduc securitatea din lumea reală la 112 biți.

Atacurile de întâlnire în mijloc sunt utile împotriva schemelor de criptare care repetă același algoritm de mai multe ori. Tehnica stochează valorile imediate de la fiecare etapă de criptare, apoi folosește aceste informații pentru a îmbunătăți radical timpul necesar pentru a forța bruta algoritmul.

Opțiunile doi și trei au chei semnificativ mai mici și sunt vulnerabile atât la atacurile cunoscute, cât și la cele selectate, precum și la altele.

Atacurile cunoscute sunt posibile atunci când un adversar are acces atât la textul de text cât și la textul text al unui mesaj. Dacă un algoritm este susceptibil la aceste atacuri, atacatorul poate utiliza aceste informații pentru a deduce cheia, ceea ce le permite să crape toate celelalte date care au fost criptate de aceeași cheie..

Un atac ales cu replică este similar, dar implică atacatorul să descopere cheia, comparând cifrele cu textele arbitrare..

Din cauza acestor vulnerabilități și a dimensiunilor generale mici ale cheilor implicate, opțiunile de introducere a tastelor două și trei sunt nesigure și nu ar trebui implementate.

Este 3DES în siguranță?

Deoarece 3DES va fi depreciat în următorii câțiva ani, cel mai bine este să folosiți alți algoritmi. Deși opțiunea de introducere a tastei una este încă considerată sigură pentru multe aplicații, nu există multe motive bune pentru care ar trebui să fie utilizată în locul unei alternative precum AES.

Deși 3DES deține un loc important în criptografie ca urmare a DES, anii săi de glorie s-au încheiat și este timpul să mergem mai departe. Dacă doriți să vă asigurați bine sistemele în viitor, ar trebui să utilizați în schimb un algoritm mai actualizat.

Legate de: Tipuri de criptare comune explicate

Planul X de licență DoD sub CC0