
Razmjena ključeva Diffie-Hellman bila je jedno od najvažnijih kretanja u kriptografiji s javnim ključem i još uvijek se često primjenjuje u nizu današnjih različitih sigurnosnih protokola.
Omogućuje dvjema strankama koje se ranije nisu sastale da sigurno utvrde ključ pomoću kojeg mogu osigurati svoju komunikaciju. U ovom ćemo članku objasniti za što se koristi, kako funkcionira korak po korak, njegove različite varijacije, kao i sigurnosna pitanja koja je potrebno imati na umu da biste ga sigurno proveli.
Što je Diffie-Hellmanova razmjena ključeva?
Razmjena ključeva Diffie-Hellman bila je prva široko korištena metoda sigurnog razvoja i razmjene ključeva preko nesigurnog kanala.
Gore se ne može činiti tako uzbudljivim ili revolucionarnim, pa neka je primjer koji objašnjava zašto je razmjena ključeva Diffie-Hellman bila tako važna prekretnica u svijetu kriptografije i zašto se ona i danas tako često koristi.
Recimo da ste tajni špijun i morate poslati neke važne podatke u svoje sjedište. Kako biste spriječili da vam neprijatelji priđu poruci?
Najčešće rješenje bilo bi šifriranje poruke kodom. Najjednostavniji način je unaprijed organizirati onu vrstu koda i tipke koju namjeravate koristiti unaprijed ili to učiniti preko sigurnog komunikacijskog kanala.
Recimo da ste posebno loš špijun, a vi i vaše sjedište odlučujete da koristite šifru za pomicanje šifri za kodiranje vaših poruka. U ovom kodu, svaki „a“ postaje „b“, svaki „b“ postaje „c“, svaki „c“ postaje „d“ i tako dalje, sve do pojave „z“ postaje „a“.
Pod ovom šifrom promjene, poruka “Idemo na večeru” postaje “Mfu nije hfu ejoofs”. Srećom, u našoj hipotetičkoj situaciji, protivnici su jednako nesposobni kao i vi i ne mogu probiti takav jednostavan kod koji im onemogućuje pristup sadržaju poruke.
Ali što se događa ako prije niste mogli dogovoriti kôd sa svojim primateljem?
Recimo da želite komunicirati sa špijunom savezničke nacije s kojim se nikada ranije niste sreli. Nemate siguran kanal preko kojeg biste razgovarali s njima. Ako ne šifrirate svoju poruku, tada će svaki protivnik koji je presreće moći pročitati sadržaj. Ako ga šifrirate bez da savezniku kažete kôd, neprijatelj ga neće moći pročitati, ali neće ni saveznik.
Ovo je pitanje bilo jedno od najvećih problema u kriptografiji sve do 1970-ih:
Kako možete sigurno razmjenjivati informacije s nekim ako niste imali priliku dijeliti ključ prije vremena?
Razmjena ključeva Diffie-Hellman bio je prvi javno korišteni mehanizam za rješavanje ovog problema. Algoritam omogućuje onima koji se nikad ranije nisu sreli da sigurno stvore zajednički ključ, čak i preko nesigurnog kanala koji protivnici mogu nadzirati.
Povijest razmjene ključeva Diffie-Hellman
Razmjena ključeva Diffie-Hellman potiče korijene još od 1970-ih. Iako se polje kriptografije značajno razvilo tijekom ranog dvadesetog stoljeća, ovo su napredovanje uglavnom usredotočeno na područje kriptografije simetričnog ključa.
Tek 1976. algoritmi javnih ključeva pojavili su se u javnoj sferi, kad su Whitfield Diffie i Martin Hellman objavili svoj rad, Novi smjerovi u kriptografiji. Suradnja je istakla mehanizme novog sustava koji bi postao poznat pod nazivom Razmjena ključeva Diffie-Hellman.
Djelo je djelomično inspirirano ranijim razvojima koje je napravio Ralph Merkle. Takozvani Merkle zagonetke uključite jednu stranu u stvaranje i slanje određenog broja kriptografskih zagonetki drugoj. Za rješavanje ovih zagonetki trebalo bi umjerena količina računskih resursa.
Primatelj bi nasumično odabrao jednu zagonetku koju treba riješiti, a zatim bi potrošio potrebni napor da je ispuni. Nakon što je zagonetka riješena, primatelju se otkrivaju identifikator i ključ sesije. Primatelj zatim šalje identifikator natrag izvornom pošiljatelju, što omogućuje pošiljatelju da zna koja je zagonetka riješena.
Budući da je izvorni pošiljatelj stvorio zagonetke, identifikator im daje do znanja koji je ključ sesije otkrio primatelj i dvije strane mogu koristiti ovaj ključ za sigurniju komunikaciju. Ako napadač prisluškuje interakciju, imat će pristup svim zagonetkama, kao i identifikatoru koji primatelj šalje natrag originalnom pošiljatelju.
Identifikator ne govori napadaču koji se ključ sesije koristi, pa je najbolji pristup za dešifriranje podataka riješiti sve zagonetke za otkrivanje ispravnog ključa sesije. Budući da će napadač u prosjeku morati riješiti polovicu zagonetki, za njih će biti puno teže otkriti ključ nego primatelju.
Ovaj pristup pruža veću sigurnost, ali još je daleko od savršenog rješenja. Razmjena ključeva Diffie-Hellman uzela je neke od ovih ideja i učinila ih složenijim kako bi se stvorila sigurna metoda kriptografije javnog ključa.
Iako je postala poznata kao razmjena ključeva Diffie-Hellman, Martin Hellman je predložio da se algoritam nazove umjesto razmjene ključeva Diffie-Hellman-Merkle, kako bi odražavao rad koji je Ralph Merkle uložio u kriptografiju s javnim ključem.
Javno se mislilo da su Merkle, Hellman i Diffie bili prvi ljudi koji su razvili kriptografiju javnog ključa do 1997. godine, kada je britanska vlada deklasificirala rad koji je početkom 1970-ih izvršio James Ellis, Clifford Cox i Malcolm Williamson.
Ispada da je trio smislio prvu shemu šifriranja javnih ključeva između 1969. i 1973., no njihov je rad klasificiran na dva desetljeća. Provedeno je pod Vladinim središtem za komunikacije (GCHQ), britanskom obavještajnom agencijom.
Njihovo otkriće zapravo je bio algoritam RSA, tako da su Diffie, Hellman i Merkle još uvijek prvi koji su razvili razmjenu ključeva Diffie-Hellman, ali više nisu prvi izumitelji kriptografije s javnim ključem.
Gdje se koristi razmjena ključeva Diffie-Hellman?
Glavna svrha razmjene ključeva Diffie-Hellman je sigurno razvijaju zajedničke tajne koje se mogu koristiti za dobivanje ključeva. Ovi se ključevi tada mogu koristiti s algoritmima simetričnih ključeva za zaštitu informacija na zaštićeni način. Simetrični algoritmi obično se koriste za šifriranje većine podataka jer su učinkovitiji od algoritama javnih ključeva.
Tehnički se razmjena ključeva Diffie-Hellman može koristiti za uspostavljanje javnih i privatnih ključeva. Međutim, u praksi se RSA obično koristi umjesto toga. To je zato što je algoritam RSA također sposoban za potpisivanje certifikata s javnim ključem, dok Diffie-Hellmanova razmjena nije.
ElGamal algoritam koji se u PGP-u uvelike koristio temelji se na razmjeni ključeva Diffie-Hellman, tako da svaki protokol koji ga koristi učinkovito implementira neku vrstu Diffie-Hellmana.
Kao jedna od najčešćih metoda za sigurnu distribuciju ključeva, razmjena ključeva Diffie-Hellman je često implementiraju u sigurnosnim protokolima kao što su TLS, IPsec, SSH, PGP i mnogi drugi. To ga čini sastavnim dijelom naših sigurnih komunikacija.
Kao dio ovih protokola, razmjena ključeva Diffie-Hellman često se koristi kako bi se osigurala veza s web stranicom, za daljinski pristup drugom računalu i za slanje šifriranih e-poruka
Kako funkcionira razmjena ključeva Diffie-Hellman?
Razmjena ključeva Diffie-Hellman je složena i može vam biti teško zaobići kako to funkcionira. Koristi vrlo veliki broj i puno matematike, nešto čega se mnogi još uvijek plaše iz tih dugih i dosadnih nastavnih sati u srednjoj školi.
Da biste stvari malo lakše razumjeli, počet ćemo objašnjavanjem razmjene ključeva Diffie-Hellman s analogijom. Nakon što imate ideju o velikoj slici kako to funkcionira, prijeći ćemo na tehnički opis osnovnih procesa.
Najbolja analogija za Diffie-Hellmanovu shemu je smišljanje dvoje ljudi koji miješaju boju. Iskoristimo kriptografski standard i recimo da su njihova imena Alice i Bob. Oboje se slažu oko slučajne boje za početak. Recimo da oni međusobno šalju poruku i odlučiti o žutoj kao zajedničkoj boji, baš kao na donjem dijagramu:
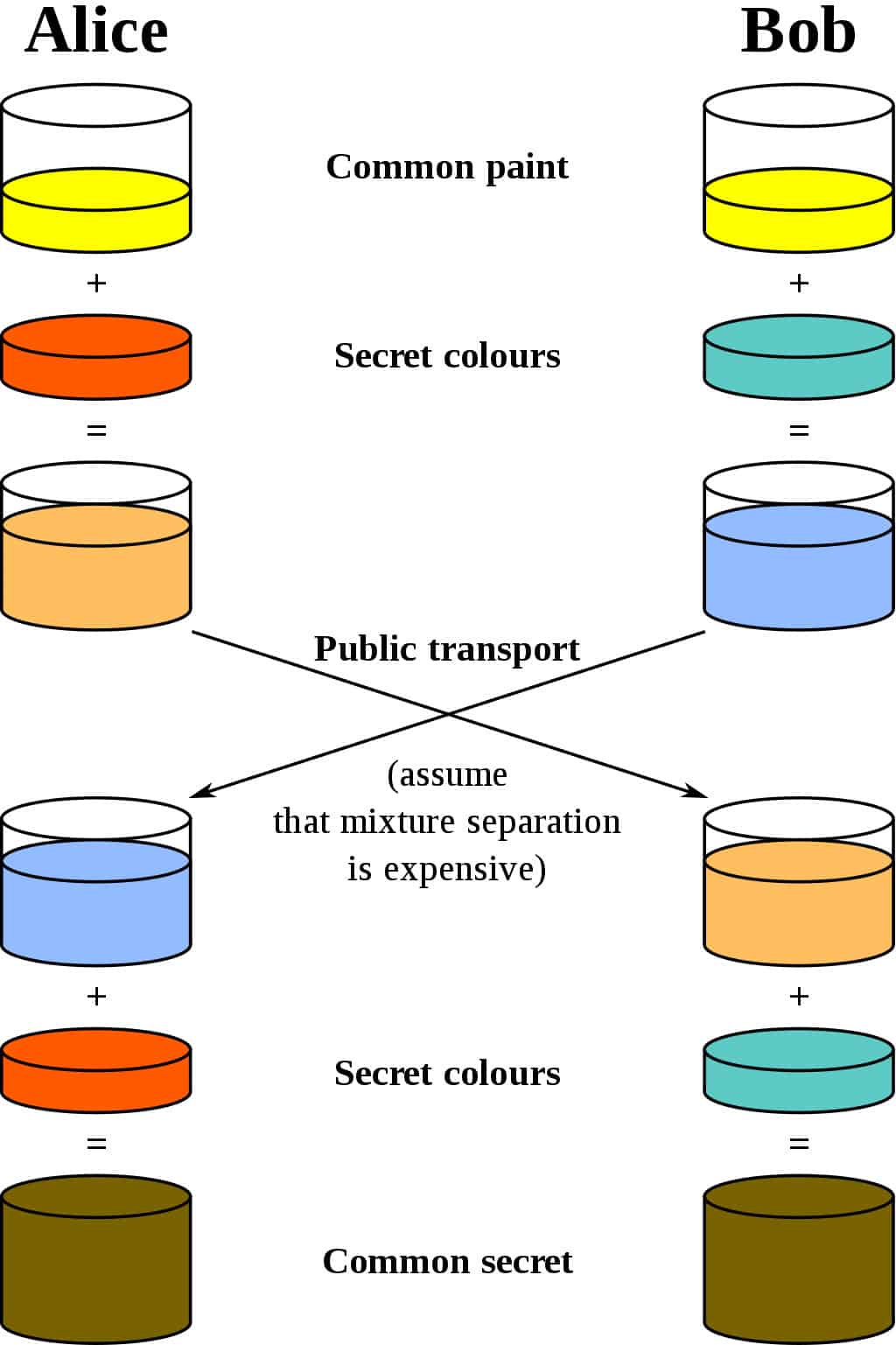
imaju svoju tajnu boju. Ne kažu drugoj strani svoj izbor. Recimo da Alice odabere Crvena, dok Bob bira a blago-zelenkasto plava.
Sljedeći je korak da i Alice i Bob izmiješaju svoju tajnu boju (crvena za Alice, zelenkasto-plava za Boba) sa žutom koja su se međusobno složili. Prema dijagramu, Alice završava an narančasta smjesa, dok je Bobov rezultat a dublje plave boje.
Kad završe sa miješanjem, rezultat šalju drugoj strani. Alice prima dublju plavu, dok Bobu se šalje boja narančaste boje.
Nakon što su od partnera dobili mješoviti rezultat, oni mu dodaju svoju tajnu boju. Alice uzima dublju plavu i dodaje joj tajnu crvenu boju, dok Bob dodaje svoju tajnu zelenkasto-plavu mješavinu naranče koju je upravo primio.
Rezultat? Oboje izlaze istom bojom, što je u ovom slučaju odvratno smeđe. Možda nije ona vrsta boje kojom biste htjeli obojiti vaš dnevni boravak, ali to je ipak zajednička boja. Ova se zajednička boja naziva ” zajednička tajna.
Kritični dio razmjene ključeva Diffie-Hellman je u tome što obje strane završavaju s istim rezultatom, bez potrebe da cijelu zajedničku tajnu pošalju preko kanala komunikacije. Odabirom zajedničke boje, njihovih vlastitih tajnih boja, razmjenom mješavine i dodavanjem vlastite boje još jednom, obje strane imaju način da dođu do iste zajedničke tajne, bez ikakvog slanja preko cijele stvari.
Ako napadač sluša razmjenu, sve što im može pristupiti je uobičajena žuta boja s kojom Alice i Bob počinju, kao i miješane boje koje se razmjenjuju. Budući da se to stvarno radi s ogromnim brojevima umjesto boja, ovi podaci nisu dovoljni da napad razluči bilo koju početnu tajnu boju, ili zajedničku tajnu (tehnički je moguće izračunati zajedničku tajnu iz ovih podataka, ali za sigurnu provedbu razmjene ključeva Diffie-Hellman trebalo bi neizvedivo vrijeme i računski resursi da se to učini).
Ovakva struktura razmjene ključeva Diffie-Hellman je ono što ga čini tako korisnim. Omogućuje dvjema stranama da komuniciraju preko potencijalno opasne veze i dalje razviju zajedničku tajnu koju mogu koristiti za izradu ključeva za šifriranje za buduće komunikacije. Nije važno slušaju li napadači jer se kompletna zajednička tajna nikada ne šalje putem veze.
Tehnički detalji razmjene ključeva Diffie-Hellman
Vrijeme je za matematiku …
Ne brinite, usporit ćemo to i pokušat ćemo cijeli proces učiniti što jednostavnijim za razumjeti. Slijedi slična pretpostavka kao gore prikazana analogija, ali umjesto miješanja i slanja boja, Diffie-Hellmanova shema zapravo izračunava na temelju izuzetno velikih pravih brojeva, a zatim ih šalje preko puta.
Da bi se osigurala sigurnost, preporučuje se da premijera (p) dugačak je najmanje 2048 bita, koji je binarni ekvivalent decimalnog broja otprilike ove veličine:
415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019
Da spriječimo da nečija glava ne eksplodira, pokrenućemo ovo objašnjenje s mnogo manjim brojevima. Budite svjesni toga razmjena ključeva Diffie-Hellman bila bi nesigurna kada bi koristila brojeve malene poput onih u našem primjeru. Mi koristimo samo tako male brojeve da bismo jednostavnije prikazali koncept.
U najosnovnijem obliku razmjene ključeva Diffie-Hellman, Alice i Bob počinju uzajamno odlučujući o dva broja za početak, za razliku od jedne uobičajene boje u gornjem primjeru. Ovi su modul (p) i baza (g).
U praktičnoj upotrebi, modul (p) je vrlo velik primarni broj, dok uporište (g) relativno je mali za pojednostavljenje izračuna. Uporište (g) je izveden iz cikličke skupine (G) koji se obično generira mnogo prije nego što se drugi koraci izvrše.
Za naš primjer, recimo da modul (p) je 17, dok je baza (g) je 4.
Nakon što se međusobno odluče o tim brojevima, Alice se dogovara o tajnom broju () za sebe, dok Bob bira svoj tajni broj (b). Recimo da odaberu:
a = 3
b = 6
Alice tada izvršava sljedeći izračun kako bi joj dala broj koji će poslati Bobu:
A = ga mod p
U gornjem proračunu, modni označava modulnu operaciju. Ovo su u osnovi proračuni kako bi se utvrdio ostatak nakon što je lijeva strana podijeljena na desnu. Kao primjer:
15 mod 4 = 3
Ako razumijete kako rade modularni postupci, sami ih možete napraviti u sljedećim izračunima, u protivnom možete koristiti mrežni kalkulator.
Pa, stavimo naše brojeve u formulu:
A = 43 mod 17
A = 64 mod 17
A = 13
Kad učinimo isto za Boba, dobivamo:
B = 46 mod 17
B = 4096 mod 17
B = 16
Tada Alice šalje svoj rezultat () Bob, dok Bob šalje njegov lik (B) do Alice. Tada Alice izračuna zajedničku tajnu (a) koristeći broj koji je dobila od Boba (B) i njen tajni broj (), koristeći sljedeću formulu:
a = Ba mod p
a = 163 mod 17
a = 4.096 mod 17
a = 16
Bob tada izvodi ono što je u osnovi isti izračun, ali s brojem koji mu je poslala Alice (), kao i svoj tajni broj (b):
a = b modni p
a = 136 mod 17
a = 4.826.809 mod 17
s = 16
Kao što vidite, obje su strane završile s istim rezultatom za a, 16. Ovo je zajednička tajna, koju samo Alice i Bob znaju. Zatim mogu to koristiti za postavljanje ključa za simetrično šifriranje, omogućujući im da sigurno šalju informacije među sebe na način da im samo oni mogu pristupiti.
Imajte na umu da iako B i a isti su u gornjem primjeru, ovo je samo slučajnost koja se temelji na malom broju koji su odabrani za ovu ilustraciju. Obično te vrijednosti ne bi bile iste u stvarnoj provedbi razmjene ključeva Diffie-Hellman.
Iako se veći dio gore navedenih podataka šalje u kanalu u jasnom tekstu (p, g, A i B) i mogu ga čitati potencijalni napadači, zajednička tajna (a) nikad se ne prenosi. Ne bi bilo praktično da napadač izračuna zajedničku tajnu (a) ili bilo koji od tajnih brojeva ( i b) iz podataka koji su poslani u jasnom tekstu.
Naravno, to pretpostavlja da je razmjena ključeva Diffie-Hellman pravilno izvedena i koristi se dovoljno velik broj. Sve dok se ove odredbe pridržavaju, razmjena ključeva Diffie-Hellman smatra se sigurnim načinom uspostavljanja zajedničke tajne koja se može koristiti za osiguranje buduće komunikacije.
Uspostavljanje zajedničkog ključa između više strana
Diffie-Hellmanova razmjena ključeva može se koristiti i za postavljanje zajedničkog ključa s većim brojem sudionika. Djeluje na isti način, osim što su potrebni daljnji krugovi izračuna da bi svaka strana dodala svoj tajni broj i završila s istom zajedničkom tajnom.
Baš kao u dvostranoj inačici razmjene ključeva Diffie-Hellman, neki dijelovi podataka šalju se preko nesigurnih kanala, ali nedovoljno da napadač može izračunati zajedničku tajnu.
Zašto je razmjena ključeva Diffie-Hellman sigurna?
Na matematičkoj razini, razmjena ključeva Diffie-Hellman oslanja se na jednosmjerne funkcije kao osnovu svoje sigurnosti. To su proračuni koji su jednostavni za napraviti na jedan način, ali mnogo teže za obrnuto.
Konkretnije, oslanja se na problem Diffie-Hellman, koji pretpostavlja da je pod pravim parametrima nemoguće izračunati gab od zasebnih vrijednosti g, g i gb. Trenutno ne postoji javno poznat način za lako pronalaženje gab od ostalih vrijednosti, zbog čega se razmjena ključeva Diffie-Hellman smatra sigurnom, unatoč činjenici da napadači mogu presresti vrijednosti p, g, , i B.
Ovjera & razmjena ključeva Diffie-Hellman
U stvarnom svijetu razmjena ključeva Diffie-Hellman rijetko se koristi sama. Glavni razlog za to je taj ne pruža provjeru autentičnosti, što korisnike čini ranjivim na napade čovjeka.
Ovi se napadi mogu dogoditi kada se razmjena ključeva Diffie-Hellman provede sama, jer nema načina da provjeri je li druga strana u vezi zaista onakva za koju kažu da je. Bez ikakvog oblika autentifikacije, korisnici se u stvari mogu povezivati s napadačima kad misle da komuniciraju sa pouzdanom strankom.
Iz tog razloga se razmjena ključeva Diffie-Hellman uglavnom provodi zajedno s nekim sredstvima autentifikacije. To često uključuje korištenje digitalnih certifikata i algoritma javnog ključa, poput RSA, za provjeru identiteta svake stranke.
Varijacije razmjene ključeva Diffie-Hellman
Razmjena ključeva Diffie-Hellman može se provesti na više različitih načina, a također je dala osnovu za nekoliko drugih algoritama. Neke od tih implementacija daju autorizaciju, dok druge imaju razne kriptografske značajke poput savršene tajnosti naprijed.
Eliptična krivulja Diffie-Hellman
Eliptična krivulja Diffie-Hellman koristi algebarsku strukturu eliptičkih krivulja kako bi omogućila njenim implementacijama da postignu sličnu razinu sigurnosti s manjom veličinom ključa. 224-bitni ključ eliptičke krivulje pruža istu razinu sigurnosti kao 2048-bitni RSA ključ. Ovo može učiniti razmjenu učinkovitijom i smanjiti zahtjeve za pohranom.
Osim manje duljine ključa i činjenice da se oslanja na svojstva eliptičkih krivulja, eliptična krivulja Diffie-Hellman djeluje na sličan način kao i standardna diffie-Hellmanova razmjena ključeva.
TLS
TLS, protokol koji se koristi da bi se osigurao veći dio interneta, može koristiti razmjenu Diffie-Hellman na tri različita načina: anonimni, statički i efemerni. U praksi treba implementirati samo efemerni Diffie-Hellman, jer ostale opcije imaju sigurnosnih problema.
- Anonimni Diffie-Hellman – Ova inačica razmjene ključeva Diffie-Hellman ne koristi provjeru autentičnosti, što ostavlja ranjivu na napade čovjeka-u-sredini. Ne treba ga koristiti ili provoditi.
- Statični Diffie-Hellman – Statički Diffie-Hellman koristi certifikate za provjeru autentičnosti poslužitelja. Ne potvrđuje autentičnost klijenta prema zadanim postavkama niti pruža tajnu prema naprijed.
- Ephemeral Diffie-Hellman – Ovo se smatra najsigurnijom provedbom jer pruža savršenu tajnu prema naprijed. Općenito se kombinira s algoritmom poput DSA ili RSA za provjeru autentičnosti jedne ili obje strane u vezi. Ephemeral Diffie-Hellman koristi različite parove ključeva svaki put kada se protokol pokrene. To daje vezi savršenu tajnu naprijed, jer čak i ako se ubuduće ugrozi ključ, on se ne može koristiti za dešifriranje svih prošlih poruka.
ElGamal
ElGamal je algoritam javnog ključa izgrađen na temelju razmjene ključeva Diffie-Hellman. Kao i Diffie-Hellman, on ne sadrži vlastite odredbe za provjeru autentičnosti te se u tu svrhu općenito kombinira s drugim mehanizmima..
ElGamal se uglavnom koristio u PGP, GNU Privacy Guard i drugim sustavima jer je njegov glavni rival, RSA, patentiran. Patent RSA-e istekao je 2000. godine, što mu je omogućilo slobodnu primjenu nakon tog datuma. Od tada se ElGamal ne provodi tako često.
STS
Stanica do stanice (STS) protokol također se temelji na razmjeni ključeva Diffie-Hellman. To je još jedan ključni plan sporazuma, no on pruža zaštitu od napada čovjeka u sredini, kao i savršenu tajnu prema naprijed.
Zahtijeva da obje strane u vezi već imaju ključ, koji se koristi za provjeru autentičnosti svake strane. Ako stranke već nisu poznate jedna drugoj, onda se potvrde mogu koristiti za potvrđivanje identiteta obje strane.
Razmjena ključeva Diffie-Hellman & RSA
Kao što smo ranije raspravljali, razmjena ključeva Diffie-Hellman često se provodi zajedno s RSA ili drugim algoritmima za pružanje autentičnosti za vezu. Ako poznajete RSA, možda se pitate zašto bi se iko gnjavio koristeći razmjenu ključeva Diffie-Hellman, budući da RSA omogućuje strankama koje se nikad ranije nisu sastale na siguran način.
RSA svojim korisnicima omogućuje šifriranje poruka javnim ključem dopisnika, tako da ih može dešifrirati samo odgovarajućim privatnim ključem. Međutim, u praksi, RSA se ne koristi za šifriranje cjeline komunikacija – bilo bi to previše neučinkovito.
Umjesto toga, RSA se često koristi samo kao sredstvo za provjeru autentičnosti obje strane. To čini sa digitalne potvrde svake stranke koje će potvrditi tijelo za certificiranje dokazati da je vlasnik certifikata doista onaj za koga kažu da je, te da javni ključ certifikata zapravo pripada njima.
Za uzajamnu provjeru autentičnosti, svaka će strana potpisati poruku koristeći svoj privatni ključ i poslati je svom komunikacijskom partneru. Svaki primatelj tada može provjeriti identitet druge strane provjerom potpisanih poruka na javnom ključu u digitalnom certifikatu njihovog komunikacijskog partnera (pogledajte gore spomenuti članak o RSA za više detalja o tome kako to funkcionira, posebno Potpisivanje poruka odjeljak).
Sada kada su obje strane potvrđene, tehnički je moguće nastaviti koristiti RSA za sigurno slanje šifriranih poruka između sebe, međutim na kraju bi bilo previše neučinkovito.
Da bi se zaobišla ta neučinkovitost, mnogi sigurnosni protokoli koriste algoritam poput razmjena ključeva Diffie-Hellman kako bi se stvorila zajednička tajna koja se može koristiti za uspostavljanje zajedničkog simetričnog ključa. Ovaj se simetrični ključ koristi u algoritmu simetričnog ključa, poput AES-a, za šifriranje podataka koje dvije strane namjeravaju sigurno poslati među sobom.
Može se činiti složenim i isprepletenim procesom, ali on završava mnogo bržim i manje zahtjevnim resursima u usporedbi s korištenjem algoritma javnog ključa za cijelu razmjenu. Ovo je zbog Šifriranje ključa simetričnog ključa naredbe je efikasnije od enkripcije javnih ključeva.
Pored neučinkovitosti koje smo upravo spomenuli, postoje i neki drugi nedostaci koji bi proizašli samo iz upotrebe RSA. RSA mu je potrebna obloga kako bi bila sigurna, pa bi se dodatni algoritam trebao adekvatno implementirati pored njega kako bi bio siguran.
RSA ne pruža savršenu tajnu prema naprijed, bilo koji, što je još jedan nedostatak u usporedbi s efemernom razmjenom ključeva Diffie-Hellman. Ti su razlozi zašto su u mnogim situacijama najbolje primijeniti RSA u kombinaciji s razmjenom ključeva Diffie-Hellman.
Alternativno, razmjena ključeva Diffie-Hellman može se kombinirati s algoritmom poput Standarda za digitalni potpis (DSS) za pružanje autentičnosti, razmjenu ključeva, povjerljivosti i provjeru integriteta podataka. U takvoj situaciji RSA nije potrebna za osiguranje veze.
Pitanja sigurnosti razmjene ključeva Diffie-Hellman
Sigurnost razmjene ključeva Diffie-Hellman ovisi o načinu njezine implementacije, kao i brojevima koji su za nju odabrani. Kao što smo gore naveli, on ne može sam autentificirati drugu stranu, ali u praksi se koriste drugi mehanizmi kojima se osigurava da druga strana u vezi nije prevarant..
Parametri za izbor broja
Ako bi implementacija Diffie-Hellmanove razmjene ključeva u stvarnom svijetu koristila brojeve malobrojne kao one u našem primjeru, to bi učinio postupak razmjene trivijalnim za napadača. Ali nije važna samo veličina brojeva – oni također trebaju biti dovoljno slučajni. Ako generator slučajnih brojeva proizvede predvidljivi izlaz, on može u potpunosti narušiti sigurnost razmjene ključeva Diffie-Hellman.
Broj p trebao bi biti dug 2048 bita da bi se osigurala sigurnost. Uporište, g, može biti relativno mali broj kao 2, ali to treba poticati iz reda G koji ima veliki glavni faktor
Napada Logjam
Razmjena ključeva Diffie-Hellman dizajnirana je na osnovu problema diskretnog logaritma koji je teško riješiti. Najučinkovitiji javno poznati mehanizam za pronalaženje rješenja je algoritam sita s brojem polja.
Mogućnosti ovog algoritma uzete su u obzir prilikom dizajniranja razmjene ključeva Diffie-Hellman. Do 1992. godine bilo je poznato da za određenu grupu, G, tri od četiri koraka koja su uključena u algoritam mogu se prethodno izračunati. Ako je taj napredak sačuvan, posljednji korak bi se mogao izračunati u relativno kratkom vremenu.
To se nije previše zabrinjavalo sve dok nije ustanovljeno da značajan dio internetskog prometa koristi iste skupine koje imaju 1024 bita ili manje. U 2015. godini akademski tim vodio je proračune za najčešći 512-bitni primetak korišten od strane Diffie-Hellmanove razmjene ključeva u TLS-u.
Oni su također mogli smanjiti 80% TLS poslužitelja koji podržavaju DHE-EXPORT, tako da su za vezu prihvatili 512-bitnu izvoznu klasu Diffie-Hellmana. Ovo znači to svaki od ovih poslužitelja podložan je napadu protivnika koji je dobro financiran.
Istraživači su nastavili s ekstrapolacijom svojih rezultata, procjenjujući da bi nacionalna država mogla srušiti 1024-bitnu premijeru. Razbijanjem jednog najčešće korištenog 1024-bitnog premijera, akademski tim procijenio je da bi protivnik mogao nadzirati 18% od milijun najpopularnijih HTTPS web stranica.
Dalje su rekli da će drugi glavni adut omogućiti protivniku da dešifrira veze 66% VPN servera i 26% SSH servera. Kasnije u izvješću akademici su sugerirali da NSA već može imati ove sposobnosti.
“Pomno čitanje objavljenih curenja iz NSA pokazuje da su napadi agencije na VPN-ove u skladu s postizanjem takvog prekida.”
Unatoč toj ranjivosti, razmjena ključeva Diffie-Hellman još uvijek može biti sigurna ako se pravilno provede. Sve dok se koristi 2048-bitni ključ, napad Logjam neće raditi. Ažurirani preglednici također su sigurni od ovog napada.
Je li razmjena ključeva Diffie-Hellman sigurna?
Iako se razmjena ključeva Diffie-Hellman može činiti složenom, ona je temeljni dio sigurne razmjene podataka na mreži. Sve dok se provodi zajedno s odgovarajućom metodom provjere autentičnosti i brojevi su pravilno odabrani, ne smatra se ranjivim za napad.
Razmjena ključeva Diffie-Hellman bila je inovativna metoda pomaganja dvije nepoznate stranke u sigurnoj komunikaciji kada je razvijena u 1970-ima. Dok sada implementiramo novije verzije s većim tipkama za zaštitu od moderne tehnologije sam protokol izgleda kao da će ostati siguran do dolaska kvantnog računanja i napredne napade koji će doći s tim.
Tehnologija cyber sigurnosti poslovanja autor: TheDigitalArtist pod licencom pod CC0