
Размяната на ключове Дифи-Хелман беше едно от най-важните разработки в криптографията с публичен ключ и тя все още често се прилага в редица съвременни протоколи за сигурност.
Тя позволява на две страни, които преди това не са се срещали, да установят сигурно ключ, който могат да използват, за да защитят своите комуникации. В тази статия ще обясним за какво се използва, как работи стъпка по стъпка, различните й вариации, както и съображенията за сигурност, които трябва да се отбележат, за да се приложи безопасно.
Каква е размяната на ключове Diffie-Hellman?
Размяната на ключове Дифи-Хелман беше първи широко използван метод за безопасно разработване и размяна на ключове по несигурен канал.
Може да не изглежда толкова вълнуващо или революционно в горните термини, така че нека дадем пример, който обяснява защо размяната на ключове Diffie-Hellman е била толкова важен етап в света на криптографията и защо тя все още се използва толкова често днес.
Нека да кажем, че сте строго секретен шпионин и трябва да изпратите важна информация в централата си. Как би попречил на враговете ви да получат съобщение?
Най-честото решение би било да се криптира съобщението с код. Най-лесният начин е да пренаредите какъв тип код и ключ, който планирате да използвате предварително, или да го направите по сигурен канал за комуникация.
Нека да кажем, че сте особено лош шпионин и вие и вашия щаб решавате да използвате слаб шифър за смяна, за да кодирате вашите съобщения. В този код всеки „a“ става „b“, всеки „b“ става „c“, всеки „c“ става „d“ и така нататък, чак до „z“ става „a“.
Под този шифър за смяна, съобщението „Нека вечеряме“ става „Mfu’t hfu ejoofs“. За щастие, в нашата хипотетична ситуация, вашите противници са също толкова некомпетентни, колкото и вие, и не са в състояние да пробият такъв прост код, който ги предпазва от достъп до съдържанието на съобщението.
Но какво се случва, ако не можахте предварително да уредите код с получателя си?
Да речем, че искате да общувате с шпионин от съюзническа нация, с когото никога не сте се срещали досега. Нямате сигурен канал, по който да говорите с тях. Ако не шифровате съобщението си, тогава всеки противник, който го прихване, ще може да прочете съдържанието. Ако го шифровате, без да кажете на кода на съюзника, тогава врагът няма да може да го прочете, но нито съюзникът.
Този брой беше един от най-големите главоблъсканици в криптографията до 1970 г.:
Как можете сигурно да обменяте информация с някого, ако не сте имали възможност да споделите ключа преди време?
Обменът на ключове Дифи-Хелман беше първият публично използван механизъм за решаване на този проблем. Алгоритъмът позволява на тези, които никога не са се срещали преди, безопасно да създадат споделен ключ, дори и по несигурен канал, който противниците може да наблюдават.
Историята на размяната на ключове Дифи-Хелман
Размерът на ключове Diffie-Hellman проследява своите корени чак през 70-те години. Докато областта на криптографията се е развила значително през по-ранния ХХ век, тези постижения са били фокусирани главно в областта на криптографията със симетричен ключ.
Едва през 1976 г. алгоритмите с публичен ключ се появиха в публичната сфера, когато Уитфийлд Дифи и Мартин Хелман публикуваха своя документ, Нови направления в криптографията. Сътрудничеството очерта механизмите на нова система, която ще стане известна като Дифи-Хелман обмен на ключове.
Работата е отчасти вдъхновена от по-ранни разработки, направени от Ралф Меркле. Така нареченият Пъзели на Меркле включете едната страна в създаването и изпращането на редица криптографски пъзели към другата. Тези пъзели ще отнемат умерено количество изчислителни ресурси за решаване.
Получателят на случаен принцип ще избере един пъзел за решаване и след това ще похарчи необходимите усилия, за да го изпълни. След като пъзелът е решен, на получателя се разкриват идентификатор и ключ за сесия. След това получателят предава идентификатора обратно на оригиналния подател, което позволява на подателя да разбере кой пъзел е решен.
Тъй като оригиналният подател е създал пъзелите, идентификаторът им позволява да разбере кой ключ на сесията е открил получателят и двете страни могат да използват този ключ за по-сигурна комуникация. Ако нападателят се вслушва във взаимодействието, той ще има достъп до всички пъзели, както и до идентификатора, който получателят предава обратно на оригиналния подател.
Идентификаторът не казва на нападателя кой ключ за сесия се използва, така че най-добрият подход за дешифриране на информацията е да решаване на всички пъзели, за да разкрие правилния ключ на сесията. Тъй като нападателят ще трябва да разреши средно половината от пъзелите, това ще им бъде много по-трудно да разкрият ключа, отколкото е за получателя..
Този подход осигурява повече сигурност, но далеч не е перфектно решение. Размяната на ключове Diffie-Hellman взе някои от тези идеи и ги направи по-сложни, за да създаде защитен метод за криптография с публичен ключ.
Въпреки че стана известна като размяна на ключове Diffie-Hellman, Мартин Hellman предложи алгоритъмът да бъде наречен вместо Diffie-Hellman-Merkle key exchange, за да отразява работата, която Ralph Merkle положи към криптографията с публичен ключ.
Публично се смяташе, че Меркъл, Хелман и Дифи са първите хора, разработили криптографията с публичен ключ до 1997 г., когато британското правителство декласира работата, извършена в началото на 70-те години от Джеймс Елис, Клифърд Кокс и Малкълм Уилямсън.
Оказва се, че триото е създало първата схема за криптиране с публичен ключ между 1969 и 1973 г., но работата им е класифицирана в продължение на две десетилетия. То се провежда в Правителствения комуникационен щаб (GCHQ), британска разузнавателна агенция.
Откритието им всъщност беше алгоритъмът RSA, така че Дифи, Хелман и Меркле все още бяха първите, които разработиха обмена на ключове Дифи-Хелман, но вече не са първите изобретатели на криптография с публичен ключ.
Къде се използва размяната на ключове Diffie-Hellman?
Основната цел на обмена на ключове Дифи-Хелман е да сигурно разработване на споделени тайни, които могат да се използват за извличане на ключове. След това тези клавиши могат да се използват със симетрични ключови алгоритми за предаване на информация по защитен начин. Симетричните алгоритми обикновено се използват за криптиране на по-голямата част от данните, тъй като те са по-ефективни от алгоритмите с публичен ключ.
Технически обменът на ключове Diffie-Hellman може да се използва за установяване на публични и частни ключове. На практика обаче RSA обикновено се използва вместо това. Това е така, защото алгоритъмът RSA също е в състояние да подписва сертификати с публичен ключ, докато размяната на ключове Diffie-Hellman не е.
Алгоритъмът ElGamal, който се използва широко в PGP, се основава на обмена на ключове Diffie-Hellman, така че всеки протокол, който го използва, ефективно прилага един вид Diffie-Hellman.
Като един от най-разпространените методи за безопасно разпространение на ключове е размяната на ключове Diffie-Hellman често се прилага в протоколи за сигурност като TLS, IPsec, SSH, PGP и много други. Това го прави неразделна част от нашите сигурни комуникации.
Като част от тези протоколи, обменът на ключове Diffie-Hellman често се използва, за да помогне за сигурността на връзката ви към уебсайт, за отдалечен достъп до друг компютър и за изпращане на криптирани имейли
Как работи обменът на ключове Diffie-Hellman?
Обменът на ключове Diffie-Hellman е сложен и може да бъде трудно да се ориентирате как работи. Използва много големи числа и много математика, нещо, което много от нас все още се страхуват от тези дълги и скучни уроци в гимназията.
За да направим нещата по-лесни за разбиране, ще започнем с обяснение на обмена на ключове Дифи-Хелман с аналогия. След като имате идея с голяма картина как работи, ще преминем към по-техническо описание на основните процеси.
Най-добрата аналогия за схемата на Дифи-Хелман е да се мисли двама души, смесващи боя. Нека използваме криптографския стандарт и да кажем, че имената им са Алис и Боб. И двамата се споразумяват за случаен цвят, за да започнете. Нека да кажем, че те изпращат взаимно съобщение и решават за жълто като техния общ цвят, точно както в диаграмата по-долу:
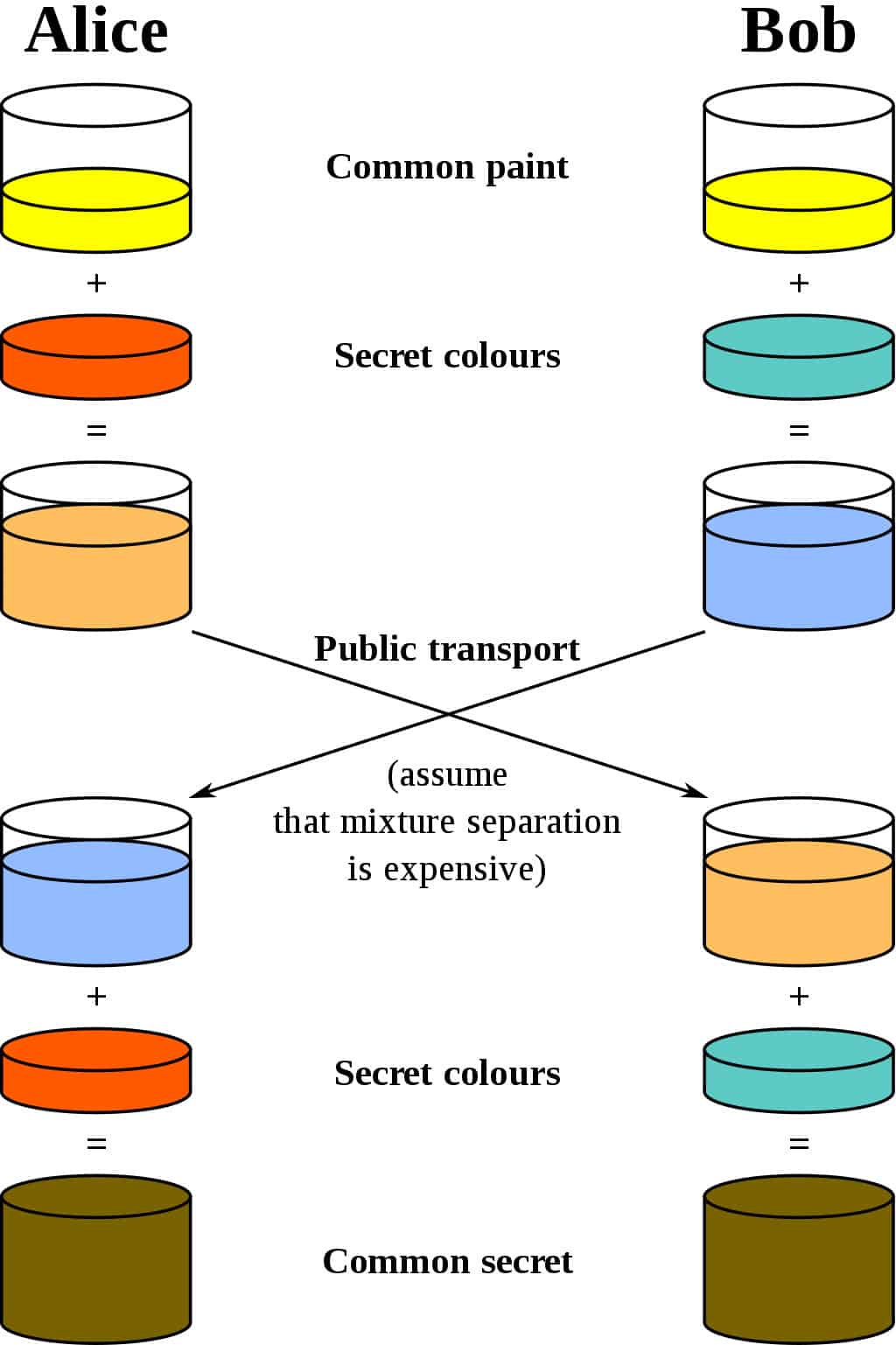
те имат свой собствен таен цвят. Те не казват на другата страна своя избор. Нека кажем, че Алиса избира червен, докато Боб избира a леко зеленикаво синьо.
Следващата стъпка е както Алис, така и Боб да смесват тайния си цвят (червен за Алиса, зеленикавосин за Боб) с жълтия, който взаимно се съгласяват. Според диаграмата, Алиса завършва с портокалов микс, докато резултатът на Боб е a по-дълбоко синьо.
След като приключат смесването, те изпращат резултата на другата страна. Алиса получава по-дълбокото синьо, докато Боб изпраща боя с оранжев цвят.
След като получат смесения резултат от партньора си, те добавят към него тайния си цвят. Алиса взема по-дълбокото синьо и добавя тайната си червена боя, докато Боб добавя тайното си зеленикаво-синьо към оранжевата смес, която току-що получи.
Резултатът? И двамата излизат с един и същи цвят, което в случая е отвратително кафяво. Може да не е от вида на цвета, с който бихте искали да рисувате хола си, но въпреки това е споделен цвят. Този споделен цвят се обозначава като обща тайна.
Критичната част от обмена на ключове Дифи-Хелман е, че и двете страни завършват с един и същ резултат, без изобщо да се налага да изпращате цялата обща тайна по комуникационния канал. Изборът на общ цвят, техните собствени тайни цветове, размяната на микса и добавянето на техния цвят още веднъж, дава на двете страни начин да стигнат до една и съща обща тайна, без изобщо да се налага да изпращате цялата работа.
Ако нападател слуша обмена, всичко, до което имат достъп, е общият жълт цвят, с който започват Алис и Боб, както и смесените цветове, които се разменят. Тъй като това наистина се прави с огромни числа вместо боя, тази информация не е достатъчна за атаката, за да открие нито един от първоначалните тайни цветове, нито общата тайна (технически е възможно да се изчисли общата тайна от тази информация, но при сигурно изпълнение на обмена на ключове Diffie-Hellman би било необходимо невъзможно количество време и изчислителни ресурси, за да се направи това).
Тази структура на обмена на ключове Дифи-Хелман е това, което го прави толкова полезен. Тя позволява на двете страни да комуникират през потенциално опасна връзка и все още да излязат с споделена тайна, която могат да използват, за да направят ключове за криптиране за бъдещите си комуникации. Няма значение дали някой нападател се слуша, защото пълната споделена тайна никога не се изпраща през връзката.
Техническите подробности при размяната на ключове Diffie-Hellman
Време е за малко математика …
Не се притеснявайте, ще го направим бавно и ще се опитаме да направим целия процес възможно най-лесен за разбиране. Следва подобно предположение като показаната по-горе аналогия, но вместо смесване и изпращане на цветове, схемата на Diffie-Hellman всъщност прави изчисления на базата на изключително големи прости числа, след което ги изпраща в цялата.
За да се гарантира сигурността, се препоръчва премиер (р) е поне 2048 бита, което е двоичен еквивалент на десетично число от около този размер:
415368757628736598425938247569843765827634879128375827365928736 84273684728938572983759283475934875938475928475928739587249587 29873958729835792875982795837529876348273685729843579348795827 93857928739548772397592837592478593867045986792384737826735267 3547623568734869386945673456827659498063849024875809603947902 7945982730187439759284620950293759287049502938058920983945872 0948602984912837502948019371092480193581037995810937501938507913 95710937597019385089103951073058710393701934701938091803984091804 98109380198501398401983509183501983091079180395810395190395180935 8109385019840193580193840198340918093851098309180019
За да предотвратим експлозия на главата на никого, ще изпълним това обяснение с много по-малки числа. Бъдете наясно с това размяната на ключове Diffie-Hellman би била несигурна, ако използва числа, малки колкото тези в нашия пример. Ние използваме само такива малки числа, за да демонстрираме концепцията по по-опростен начин.
В най-основната форма на размяната на ключове Diffie-Hellman, Алис и Боб започват, като взаимно решават две числа, с които да започнат, за разлика от единичната обикновена боя в примера по-горе. Това са модулът (р) и основата (г).
В практическа употреба, модулът (p) е много голямо просто число, докато базата (г) е сравнително малко за опростяване на изчисленията. Базата (г) е получена от циклична група (G), което обикновено се генерира доста преди да се извършат другите стъпки.
За нашия пример, нека кажем, че модулът (р) е 17, докато основата (г) е 4.
След като взаимно вземат решение за тези номера, Алис се урежда на секретен номер (а) за себе си, докато Боб избира свой секретен номер (б). Нека да кажем, че те избират:
a = 3
b = 6
След това Алис извършва следното изчисление, за да й даде номера, който ще изпрати на Боб:
A = ga mod p
В горното изчисление, моден означава модулна операция. Това са по същество изчисления, за да се установи останалото след разделяне на лявата страна на дясната. Като пример:
15 мод 4 = 3
Ако разбирате как действат модулните операции, можете да ги направите сами в следните изчисления, в противен случай можете да използвате онлайн калкулатор.
Така че нека да поставим нашите номера във формулата:
A = 43 мод 17
A = 64 мод 17
A = 13
Когато направим същото за Боб, получаваме:
B = 46 мод 17
B = 4096 мод 17
B = 16
След това Алис изпраща резултата си (А) на Боб, докато Боб изпраща фигурата си (B) до Алиса. Тогава Алис изчислява споделената тайна (с) използвайки номера, който тя получи от Боб (B) и нейният секретен номер (а), използвайки следната формула:
с = Ba mod р
с = 163 мод 17
с = 4 096 мода 17
с = 16
След това Боб извършва това, което по същество е едно и също изчисление, но с номера, който му изпрати Алиса (А), както и собствения му секретен номер (б):
с = Аб моден р
с = 136 мод 17
с = 4 826 809 мод 17
s = 16
Както можете да видите, и двете страни завършиха с един и същи резултат за с, 16. Това е споделената тайна, която само Алис и Боб знаят. След това те могат да използват това, за да настроят ключ за симетрично криптиране, което им позволява безопасно да изпращат информация помежду си по начин, който само те да имат достъп до нея.
Имайте предвид, че въпреки че B и с са същите в примера по-горе, това е просто съвпадение, основано на малките числа, избрани за тази илюстрация. Обикновено тези стойности не биха били еднакви при реална реализация на размяната на ключове Diffie-Hellman.
Въпреки че голяма част от горните данни се изпращат по канала в ясен текст (p, g, A и B) и може да бъде прочетена от потенциални нападатели, споделената тайна (с) никога не се предава. Не би било практично за нападател да изчисли споделената тайна (с) или някой от секретните номера (а и б) от информацията, която е изпратена в ясен текст.
Разбира се, това предполага, че обменът на ключове Diffie-Hellman е правилно реализиран и се използват достатъчно големи числа. Докато се спазват тези разпоредби, обменът на ключове Diffie-Hellman се счита за безопасен начин за установяване на споделена тайна, която може да се използва за осигуряване на бъдещи комуникации.
Установяване на споделен ключ между множество страни
Размяната на ключове Diffie-Hellman може да се използва и за настройка на споделен ключ с по-голям брой участници. Тя работи по същия начин, с изключение на това, че са необходими допълнителни кръгове от изчисленията, за да може всяка страна да добави секретния си номер и да завърши със същата споделена тайна.
Точно както в двустранната версия на обмена на ключове Diffie-Hellman, някои части от информацията се изпращат по несигурни канали, но не са достатъчни, за да може един нападател да може да изчисли споделената тайна.
Защо е сигурна обмяната на ключове Diffie-Hellman?
На математическо ниво обменът на ключове Diffie-Hellman разчита на еднопосочни функции като основа за неговата сигурност. Това са изчисления, които са прости по един начин, но много по-трудни за изчисляване в обратен ред.
По-конкретно, той разчита на проблема Дифи-Хелман, който предполага, че при правилните параметри е невъзможно да се изчисли габ от отделните стойности на г, га и гб. Понастоящем няма обществено известен начин за лесно намиране габ от другите стойности, поради което обменът на ключове Diffie-Hellman се счита за сигурен, въпреки факта, че нападателите могат да прихващат стойностите р, г, А, и B.
заверка & размяната на ключове Дифи-Хелман
В реалния свят, обменът на ключове Diffie-Hellman рядко се използва от само себе си. Основната причина за това е тази тя не предоставя автентификация, което оставя потребителите уязвими към атаки от човек в средата.
Тези атаки могат да се извършват, когато обменът на ключове Дифи-Хелман се осъществи сам, защото няма средства за проверка дали другата страна във връзка наистина е такава, за която казват, че е. Без никаква форма на удостоверяване, потребителите всъщност могат да се свързват с нападатели когато смятат, че общуват с доверена страна.
Поради тази причина обменът на ключове Diffie-Hellman обикновено се осъществява заедно с някои средства за удостоверяване. Това често включва използване на цифрови сертификати и алгоритъм с публичен ключ, като RSA, за да се провери самоличността на всяка страна.
Вариации на размяната на ключове Дифи-Хелман
Обменът на ключове Diffie-Hellman може да бъде реализиран по много различни начини, а също така е дал основа за няколко други алгоритми. Някои от тези реализации предоставят разрешение, докато други имат различни криптографски функции, като перфектна тайна за напред.
Елиптична крива Дифи-Хелман
Елиптичната крива Diffie-Hellman се възползва от алгебраичната структура на елиптичните криви, за да позволи на нейните реализации да постигнат подобно ниво на сигурност с по-малък размер на ключа. 224-битов ключ с елиптична крива осигурява същото ниво на сигурност като 2048-битов RSA ключ. Това може да направи обмена по-ефективен и да намали изискванията за съхранение.
Освен по-малката дължина на ключа и факта, че разчита на свойствата на елиптичните криви, елиптичната крива Diffie-Hellman работи по подобен начин на стандартната размяна на ключове Diffie-Hellman.
TLS
TLS, който е протокол, който се използва за осигуряване на голяма част от интернет, може да използва обмена Diffie-Hellman по три различни начина: анонимен, статичен и ефемер. На практика трябва да се прилага само ефемерна Дифи-Хелман, тъй като другите опции имат проблеми със сигурността.
- Анонимен Дифи-Хелман – Тази версия на размяната на ключове Diffie-Hellman не използва никаква проверка на автентичността, което я прави уязвима за атаки от човек в средата. Не трябва да се използва или прилага.
- Статичен Дифи-Хелман – Static Diffie-Hellman използва сертификати за удостоверяване на сървъра. Той не удостоверява клиента по подразбиране, нито предоставя предавателна тайна.
- Ефемерна Дифи-Хелман – Това се счита за най-сигурното изпълнение, тъй като осигурява перфектна тайна за напред. Обикновено се комбинира с алгоритъм като DSA или RSA за удостоверяване на едната или двете страни в връзката. Ephemeral Diffie-Hellman използва различни двойки ключове при всяко изпълнение на протокола. Това дава на връзката перфектна секретност за напред, защото дори и ключ да бъде компрометиран в бъдеще, той не може да бъде използван за декриптиране на всички минали съобщения.
ElGamal
ElGamal е алгоритъм с публичен ключ, изграден на основата на размяната на ключове Diffie-Hellman. Подобно на Diffie-Hellman, тя не съдържа разпоредби за автентификация самостоятелно и обикновено се комбинира с други механизми за тази цел.
ElGamal се използва главно в PGP, GNU Privacy Guard и други системи, тъй като основният му конкурент, RSA, е патентован. Патентът на RSA изтече през 2000 г., което позволи свободното му прилагане след тази дата. Оттогава ElGamal не се прилага толкова често.
STS
Протоколът от станция до станция (STS) също се основава на обмена на ключове Diffie-Hellman. Това е друга ключова схема на споразумение, но тя осигурява защита срещу атаки от човек в средата, както и перфектна тайна за напред.
Изисква и двете страни във връзката вече да имат ключ, който се използва за удостоверяване на всяка страна. Ако страните вече не са познати една на друга, тогава сертификатите могат да бъдат използвани за валидиране на самоличността на двете страни.
Размяната на ключове Дифи-Хелман & RSA
Както обсъждахме по-рано, обменът на ключове Diffie-Hellman често се осъществява заедно с RSA или други алгоритми за осигуряване на удостоверяване на връзката. Ако сте запознати с RSA, може би се чудите защо някой би си направил труда да използва и размяната на ключове Diffie-Hellman, тъй като RSA дава възможност на страните, които никога преди не са се срещали, да общуват сигурно.
RSA позволява на своите потребители да криптират съобщения с публичния ключ на кореспондента си, така че да могат да бъдат дешифрирани само от съответстващия частен ключ. На практика обаче, RSA не се използва за криптиране на цялата комуникация – това би било твърде неефективно.
Вместо това RSA често се използва само като средство за удостоверяване на двете страни. Това прави това с цифровите сертификати на всяка страна, които ще бъдат проверени от сертифициращ орган да докаже, че притежателят на сертификат наистина е такъв, за когото казват, че е и че публичният ключ в сертификата всъщност им принадлежи.
За взаимно удостоверяване, всяка страна ще подпише съобщение чрез личния си ключ и след това ще го изпрати на своя партньор за комуникация. Всеки получател може след това проверете самоличността на другата страна, като проверите подписаните съобщения срещу публичния ключ на цифровия сертификат на техния партньор за комуникация (вижте горепосочената статия за RSA за повече подробности за това как работи, по-специално Подписване на съобщения раздел).
След като двете страни са удостоверени, технически е възможно да продължите да използвате RSA за безопасно изпращане на криптирани съобщения помежду си, но в крайна сметка това ще бъде твърде неефективно.
За да заобиколят тази неефективност, много протоколи за сигурност използват алгоритъм като размяната на ключове Diffie-Hellman, за да излезе с обща тайна, която може да се използва за установяване на споделен симетричен ключ. Този симетричен ключ след това се използва в алгоритъм на симетричен ключ, като AES, за криптиране на данните че двете страни възнамеряват да изпращат сигурно помежду си.
Може да изглежда сложен и объркан процес, но в крайна сметка той е много по-бърз и по-малко взискателен към ресурсите в сравнение с използването на алгоритъм с публичен ключ за цялата размяна. Това е така, защото Шифрирането на симетричен ключ е порядък по-ефективен от криптирането с публичен ключ.
В допълнение към неефективността, която току-що споменахме, има някои други недостатъци, които биха дошли само от използването на RSA. RSA се нуждае от подплънки, за да е сигурен, така че трябва да се приложи подходящ алгоритъм заедно с него, за да го направи безопасен.
RSA не осигурява перфектна тайна за напред, или, което е друг недостатък в сравнение с ефемерната размяна на ключове Diffie-Hellman. Колективно тези причини са защо в много ситуации е най-добре да се прилага само RSA във връзка с размяната на ключове Diffie-Hellman.
Алтернативно, обменът на ключове Diffie-Hellman може да се комбинира с алгоритъм като Digital Digital Signature Standard (DSS) за осигуряване на удостоверяване, обмен на ключове, конфиденциалност и проверка на целостта на данните. В такава ситуация RSA не е необходима за осигуряване на връзката.
Проблеми със сигурността на размяната на ключове Diffie-Hellman
Сигурността на обмена на ключове Diffie-Hellman зависи от начина на реализация, както и от избраните за нея числа. Както посочихме по-горе, той няма средства за автентификация на другата страна, но на практика се използват други механизми, за да се гарантира, че другата страна във връзка не е измамник.
Параметри за избор на номер
Ако реализирането на реалния свят на обмена на ключове Diffie-Hellman използваше числа, по-малки от тези в нашия пример, това би направило процеса на обмен тривиален за нападателя да се спука. Но не само размерът на числата има значение, но и номерата трябва да са достатъчно случайни. Ако генератор на произволни числа произведе предсказуем изход, това може напълно да подкопае сигурността на обмена на ключове Diffie-Hellman.
Броя р трябва да е 2048 бита за да се гарантира сигурността. Базата, г, може да бъде сравнително малък брой като 2, но трябва да идва от заповед от G това има голям основен фактор
Атаката на Лоджам
Размерът на ключове Diffie-Hellman е проектиран на базата на трудно разрешим дискретен логаритъм. Най-ефективният обществено известен механизъм за намиране на решението е алгоритъмът на сито с числово поле.
Възможностите на този алгоритъм бяха взети под внимание при проектирането на обмена на ключове Diffie-Hellman. До 1992 г. се знае, че за дадена група, G, три от четирите стъпки, включени в алгоритъма, потенциално могат да бъдат изчислени предварително. Ако този напредък беше запазен, последната стъпка може да бъде изчислена в сравнително кратко време.
Това не беше твърде притеснително, докато не се разбра, че значителна част от интернет трафика използва същите групи, които са 1024 бита или по-малки. През 2015 г. академичен екип проведе изчисленията за най-често срещания 512-битов премиер, използван от размяната на ключове Diffie-Hellman в TLS.
Те също бяха в състояние да понижат 80% от TLS сървърите, които поддържат DHE-EXPORT, така че да приемат 512-битов клас за обмен на Diffie-Hellman с експорт за връзка. Това означава, че всеки от тези сървъри е уязвим за атака от страна на добре съхранен противник.
Изследователите продължиха да екстраполират своите резултати, изчислявайки, че национална държава може да счупи 1024-битов премиер. Разбивайки единствения най-често използван 1024-битов премиер, академичният екип прецени, че противник може да наблюдава 18% от милиона най-популярни HTTPS уебсайтове.
Те казаха, че вторият премиер ще даде възможност на противника да декриптира връзките на 66% от VPN сървърите и 26% от SSH сървърите. По-късно в доклада учените предположиха, че НСА може вече да има тези възможности.
„Отблизо четене на публикувани течове на NSA показва, че атаките на агенцията срещу VPN са съвместими с постигането на подобна почивка.“
Въпреки тази уязвимост, размяната на ключове Diffie-Hellman все още може да бъде сигурна, ако е внедрена правилно. Докато се използва 2048-битов ключ, атаката на Logjam няма да работи. Актуализираните браузъри също са защитени от тази атака.
Безопасна ли е обмяната на ключове Diffie-Hellman?
Въпреки че обменът на ключове Diffie-Hellman може да изглежда сложен, той е основна част от сигурния обмен на данни онлайн. Докато той е реализиран заедно с подходящ метод за удостоверяване и номерата са избрани правилно, не се счита за уязвим за атака.
Размяната на ключове Diffie-Hellman беше иновативен метод за подпомагане на две неизвестни страни да общуват безопасно, когато е разработен през 70-те години. Докато сега прилагаме по-нови версии с по-големи клавиши, за да се предпазим от съвременните технологии самият протокол изглежда сякаш ще продължи да бъде сигурен до пристигането на квантовите изчисления и напредналите атаки, които ще дойдат с него.
Бизнес технология за киберсигурност от TheDigitalArtist, лицензиран съгласно CC0