Какво представляват цифровите подписи и как работят?

Цифровите подписи са като електронни версии на вашите ръкописни подписи. Те позволяват на хората да проверяват автентичност и цялост на данните, както и да попречи на подписалия да може да отхвърли (откаже) участието си.

Тези свойства доведоха до приемането на цифрови подписи в широк спектър от приложения, включително много от нашите протоколи за сигурност, сигурен имейл и в управлението на цифрови права.

В тази статия ще обсъдим какви са цифровите подписи, където се използват, както и техническите подробности за два от най-популярните алгоритми, RSA и DSA.

Какво представляват цифровите подписи?

Както бе посочено по-горе, цифровите подписи ни предоставят три много важни свойства. Това са удостоверяване, цялостност и неотхвърляне.

заверка е процесът на проверка дали човекът, който изпраща съобщение, наистина е такъв, за когото казват, че е, а не измамник.

Най- интегритет на данни или съобщение се отнася до това дали е пристигнало в същото състояние, както когато е изпратено. Ако съобщението е променено или подправено, то вече не запазва целостта си.

Ако има данни или съобщение не-repudiable, това означава, че неговият автор не може да оспори, че те са били истинският създател на документа. Този имот отнема правдоподобна опровержимост или старото извинение „Съжалявам, приятелят ми използва акаунта ми“.

Докато личният ключ на индивида не е компрометиран, цифровите подписи могат да предоставят и трите тези свойства на данни.

Може би се чудите защо на първо място се нуждаем от тези свойства. Нека да направим крачка назад и да помислим как правим нещата в среща лице в лице.

Да речем, че дължите на приятеля си Майк 100 долара. Ти си добър човек, така че се радваш да му го върнеш, когато получиш парите.

Най-добрият начин да го направите е просто да дадете сметка на 100 долара на Майк. Познавате го от години и знаете как изглежда, така би било лесно да потвърдите самоличността си и по този начин да удостоверите, че давате парите на точния човек.

Ако сте били наистина анален, можете дори да проверите личната му карта и да го накарате да подпише ръкописна разписка за вас. Подписът върху разписката би я придал целостност и би я направил неподлежаща на повторение.

Ами ако вместо да извършите транзакцията лице в лице, получите обаждане от някой, който казва, че те са Майк и че трябва да изпратите 100 долара на номер на сметка 12345678.

„Но не приличаш на Майк“, казваш.

“Имам настинка. Изпратете го сега, имам нужда от парите. “

Бихте ли изпратили парите? Вероятно не.

Няма начин да разберем дали наистина е Майк или правилния номер на акаунта. За всичко, което знаете, може да е самозванец, който се опитва да открадне от вас. Вместо да превеждате парите веднага, най-добре би било да изчакате, докато видите Майк, за да можете да му дадете парите лично.

Точно както в горния сценарий, често се сблъскваме със ситуации, в които трябва проверете самоличността на дадена страна или целостта на данните в онлайн света. Ето защо цифровите подписи са станали като механизъм, който може да предостави тези свойства и да улесни сигурните онлайн транзакции.

Без тях може да не знаем с кого говорим, не бихме могли да сме сигурни дали данните са били подправени или не и човекът може да отрече, че носи отговорност.

Използването на цифровия подпис

Тези свойства на цифровия подпис ги правят полезни в голямо разнообразие от приложения. Те често се използват сами или заедно с криптиране в редица различни протоколи за сигурност, като например:

• IPsec
• SSH
• TLS

Те често се използват и при управление на цифровите права, в blockchain технология, в управление на договори приложения, като част от софтуерна дистрибуция, и в финанси.

История на цифровите подписи

Идеята за дигиталните подписи за пръв път се разпространи от известните криптографи Уитфийлд Дифи и Мартин Хелман в своята книга от 1976 г. Нови направления в криптографията. През 1978 г. Роналд Ривест, Ади Шамир и Лен Адлеман внесоха в публичен изглед алгоритъма на RSA, който може да се използва за създаване на несигурни цифрови подписи.

Отне още десетилетие, за да се появят цифрови подписи в широко разпространено приложение: издаването на IBM Lotus Notes 1.0. От този момент нататък цифровите подписи започнаха да виждат все по-широко приемане, тъй като се появяват нови техники и необходимостта от онлайн проверка на автентичността и проверка на целостта.

Кратко представяне на криптографията с публичен ключ

Преди да преминем към цифрови подписи, най-добре е да обхванем някои от важните аспекти на криптографията с публичен ключ, които формират основата на работата на цифровия подпис.

Ако сте сравнително нови в криптографията, системата, с която ще бъдете най-запознати, е криптиране на симетричен ключ. Това просто означава, че един и същ ключ (който е подобен на парола, но има някои разлики) се използва както за криптиране, така и за декриптиране на данни.

Шифроването с публичен ключ беше революция, защото включваше използвайки отделни ключове за процеса на криптиране и декриптиране, което води до редица различни криптографски приложения. Тези два клавиша образуваха двойка ключове, състояща се от публичен ключ и частен ключ. Публичният ключ очевидно може да бъде споделен публично, докато частният ключ трябва да се пази в тайна, за да може системата да бъде защитена.

Двете най-често използвани криптографии с публичен ключ са криптиране и цифров подпис.

Encryption

Една от основополагащите характеристики на криптографията с публичен ключ беше тази тя позволява на страните, които никога не са се срещали, да изпращат поверително съобщения един на друг. Подателят търси публичния ключ на желания от тях получател (те могат да бъдат намерени на сървъри с публични ключове, на лични уебсайтове или просто като попитате отделния човек), след което криптира съобщение с този ключ, преди да го изпрати на получателя.

Получателят е единственият човек, който може да получи достъп до съобщението – ако приемем, че частният ключ не е компрометиран – като го декриптира с личния си ключ. Въпреки че публичният ключ е използван за криптиране на съобщението, той може да бъде дешифриран само от частния ключ. Ако получателят желае да отговори, той намира публичния ключ на оригиналния подател, след което повтаря процеса.

Вижте също: Обяснени общи типове кодиране

Как работят цифровите подписи?

Както казахме, дигиталните подписи се използват за удостоверяване, за да се види дали данните са били подправени и да се предостави неотхвърляне. Съществуват редица различни механизми, които могат да се използват за цифрови подписи и всеки от тях има малки разлики в структурата си.

По принцип тези алгоритми трябва да се състоят от три под-алгоритми:

• Алгоритъм за генериране на ключове – Този алгоритъм генерира произволна двойка ключове за потребител. Числата, участващи в двойката ключове, трябва да спазват определени параметри, за да се считат за сигурни. Два от най-важните аспекти са, че числата са достатъчно случайни и адекватно оразмерени.
• Алгоритъм за подписване на данни – След като потребителят има своите ключове, има специфични начини за това как те се прилагат към данните в процеса на подписване.
• Алгоритъм за проверка на подписа – По същия начин проверката на подпис следва предварително определен процес.

За да бъде ефективна системата за цифров подпис, тя трябва да бъде структурирана по такъв начин, че:

• Данните, подписани с частен ключ, са потвърдено с съответния публичен ключ на същия индивид.
• По същество би трябвало да е невъзможно (използвайки съвременни технологии и техники) да подправите валиден подпис, без да знаете личния ключ на индивида.

Някои от най-разпространените схеми за цифров подпис включват RSA, DSA, EcDSA и EdDSA.

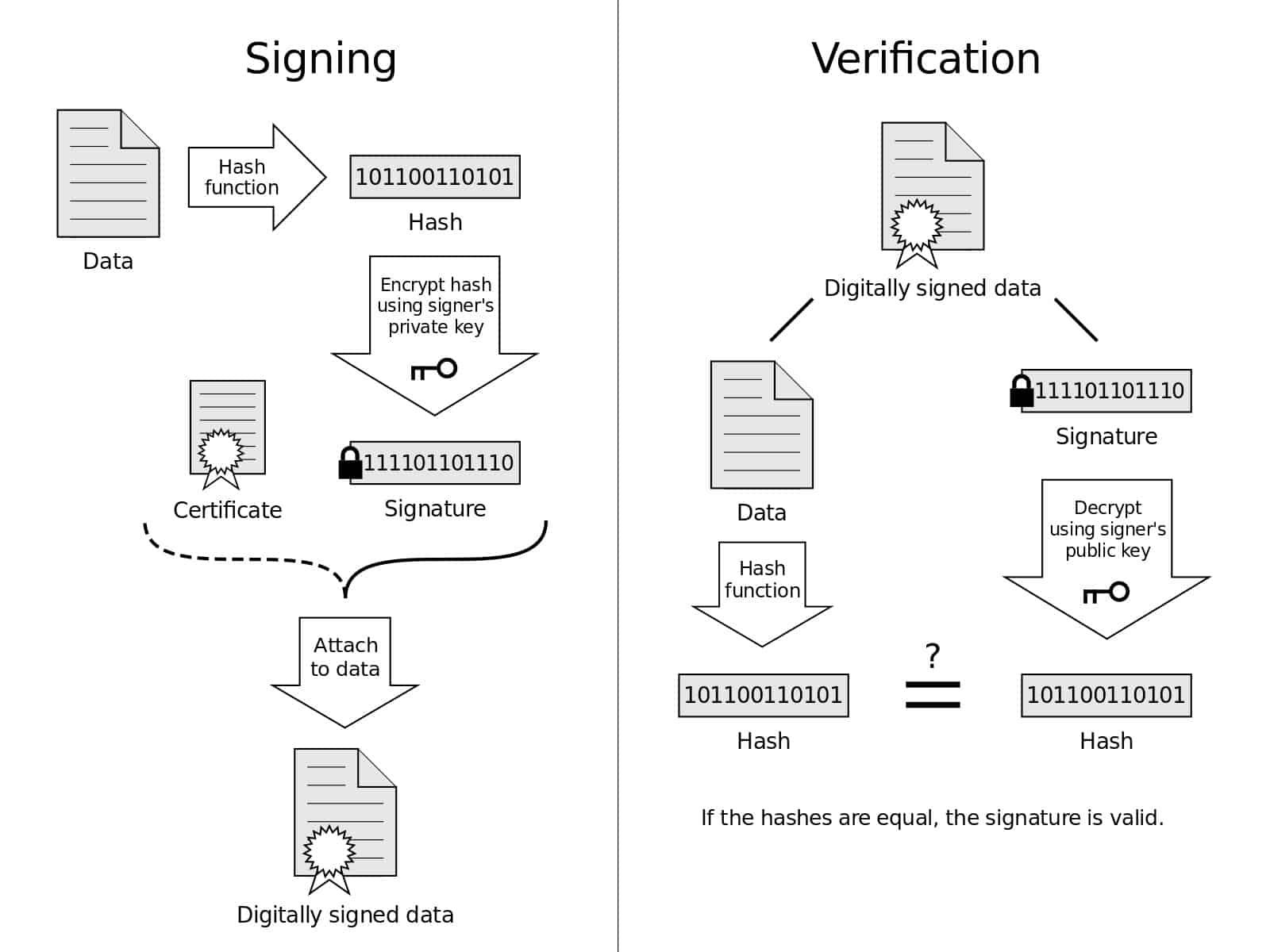
Това изображение дава визуално представяне на процесите на подписване и проверка. Диаграма за цифров подпис от Acdx, лицензиран съгласно CC0

RSA

RSA беше първият алгоритъм за цифров подпис, но той може да се използва и за криптиране с публичен ключ. В тази статия ще прескочим аспекта на криптирането, но можете да разберете повече за това в нашата обширна статия, която обхваща какво е RSA и как работи.

RSA ключово поколение

При сигурни реализации на RSA, ключовите двойки обикновено се установяват автоматично при следния процес:

Първо поколение

Избират се две индивидуални прости числа, р и р. Точният размер на тези прайсове ще варира в зависимост от размера на ключа. В наши дни минимум 2048-битови RSA ключове обикновено се препоръчват за адекватна сигурност, така че говорим за две прости числа, които се умножават, за да се получи 2048-битово число.

2048 бита е размер в двоичната система с числа. Ако число от този размер беше преобразувано в по-познатата ни десетична система, това ще бъде приблизително толкова дълго:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Праймерите в RSA трябва да бъдат избрани на случаен принцип и трябва да имат сходни дължини.

В нашия пример ще използваме много по-малки числа, за да улесним нещата. Имайте предвид, че използването на клавиши с такъв размер би направило цифровите подписи тривиални за фалшиви. Ето защо толкова големи стойности се използват на практика.

Нека да кажем, че:

р = 13

р = 17

Първата стъпка ще бъде изчисляването на модула н използвайки следната формула:

n = pq

н = 13 х 17

н = 221

Стойността на н е и дължината на ключа.

Тотисната функция на Carmichael

Сега, когато имаме стойността за н, следващата стъпка е да използвате тотинг функцията на Carmichael:

λ(н) = НОК (р – 1, р – 1)

Има няколко неща, които трябва да разберете:

• λ(н) означава тотиент на Carmichael за стойността на н
• НОК представлява най-ниският общ множител. Това е най-ниското общо число, което и двете р-1 и р-1 може да се раздели на

Нека включим нашите фигури в уравнението:

λ(221) = НОК (13 – 1, 17 – 1)

λ(221) = НОК (12, 16)

Ако сте добър в психическата математика, може би сте разбрали това 48 е най-ниският общ множител и на двете 12 и 16. Това е така, защото 48 е най-малкото число, в което и двете от тези числа могат да се поберат (12 x 4 = 48, 16 x 3 = 48). Следователно:

λ(221) = 48

Създаване с публичния ключ

В RSA публичният ключ се състои от стойността н (което вече сме изчислили като 221) и д. Тъй като публичният ключ се споделя свободно, стойността за д не трябва да е тайна Всъщност на практика често се задава 65 657, защото по-големите числа ще забавят процеса на криптиране. В нашия пример ще настроим д до 5, само за да го направите малък и прост номер за работа.

Следователно публичният ключ за този пример се състои от 221 и 5. Ще разгледаме спецификите за това как се прилага публичният ключ в следващите раздели.

Измисляне на частния ключ

Точно както публичният ни ключ е съставен от две номера, така и личният ни ключ. Частните ключове се състоят от д и д. Вече знаем стойността за д (5), и можем да използваме следната формула, за да намерим д:

д = 1 /д моден λ(н)

Отбележи, че моден просто символизира модулна операция, което обикновено означава, че трябва да намерите остатъка, след като разделите лявата страна на дясната. Като пример:

17 мод 3 = 2

Това е така, защото 3 се вписват в 17 общо 5 пъти, а в остатък 2.

Примерът ни е малко по-различен. The „1 /д моденМоже да изглежда, че сегментът на уравнението ви казва да разделите 1 от д, но всъщност не е. Това е объркващо, но това е начин за представяне на модулна обратна. Уравнението всъщност ни казва да изчислим модулния обрат на д и λ(н).

Модулната обръщане обикновено се извлича с помощта на разширения евклидов алгоритъм, но няма да покриваме това в тази статия. Вместо това ние просто ще използваме онлайн калкулатор, за да улесним нещата.

Сега, след като сме го измъкнали, нека въведем стойностите си във формулата:

д = 1/5 мод 48

Да намеря д, всичко, което трябва да направим, е да въведем нашата стойност за д (5) в онлайн калкулатора, където пише цяло число, тогава нашата стойност за λ(н), кое е 48, където пише модул.

Това ни дава резултат от 29 според онлайн калкулатора. Следователно, нашият частен ключ ще се състои от:

д = 5

д = 29.

След като генерирахме и двата ни ключа, следващият въпрос е: „Какво правим с тях?“ Е, бихме могли да ги използваме за криптиране и дешифриране на съобщения чрез криптография с публичен ключ, но тази статия е за цифровите подписи, така че ще се съсредоточим върху това.

Цифрово подписване на данни с RSA

Нека да кажем, че някой иска да изпрати съобщение до своя приятел, но иска да се увери, че приятелят може да провери автентичността и целостта на съобщението. Те биха могли да направят това, като използват цифров подпис RSA за подписване на съобщението.

Първата стъпка е да изпълнете цялото съобщение чрез хеш функция. Това са еднопосочни функции, които винаги дават един и същ изход за даден вход. Защитните хеш функции по същество е невъзможно да се обърне, което означава, че изходът не може да бъде използван за определяне на входа. Освен това е невъзможно две отделни съобщения да имат еднакъв изход.

Можете да разберете повече за хеш функциите в Какво е хеширане? Раздел на нашата статия, Шифроване, хеширане, осоляване – каква е разликата?

Да речем, че искаме да подпишем цифрово съобщението „Горещо е днес“, Така че нашият получател да знае дали съобщението е автентично или не и дали е било подправено. Така че ние бягаме „Горещо е днес”Чрез хеш функция.

Разбиране на хеш функциите

В наши дни най-често използваната функция за сигурен хеш е SHA-256. Когато поставим нашето съобщение чрез онлайн калкулатор SHA-256, той ни дава резултат като този:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Това поражда няколко проблема за нашия пример. Първата е, че тя не е десетично число като тези, с които повечето хора са свикнали. Може би сте забелязали, че в този номер има букви и че те се изкачват само е. Това ни дава представа, че това всъщност е шестнадесетично число.

Най- шестнадесетичната система разчита на база 16, а не на 10, като системата с числа, която обикновено използваме. Това означава, че вместо да се брои в кратни на 10, той се брои в кратни на 16, а първите 6 букви от нашата азбука се използват за съставяне на тези допълнителни числа. Брой като този може да бъде преобразуван в ежедневната ни десетична система, но това е извън обхвата на тази статия.

Вторият проблем, който имаме е, че това е наистина голям брой. Ако беше преобразуван в десетична, щеше да е още по-дълъг. Тъй като в това ръководство се стремим към простота, провеждането на изчисленията с толкова голям брой би направило нещата твърде объркващи, за да получат основните понятия в.

С идеята да покажем как RSA цифровите подписи работят по лесен за разбиране начин, в следващия пример няма да използваме толкова голяма хеш стойност. Вместо това ще се преструваме, че хеш стойността на „Горещо е днес”Е просто 10.

Ние също така ще трябва да се преструваме, че като всеки истински хеш, всеки път, когато поставим нашия принос на „Днес е горещо“ чрез функцията хеш, той винаги ще връща стойността на 10. За да бъдем съгласувани с това как нормално функционират хеш функциите, ще трябва да се преструваме, че е невероятно малко за всеки друг принос да даде същата стойност. По подобен начин трябва да се преструваме, че също не е възможно да разберем нашия първоначален принос от тази стойност. Тези свойства са това, което прави хешите изключително полезни.

Как личният ключ на изпращача се използва за цифрово подписване на хеш стойността

Нашият подател въведе тяхното съобщение, след което го постави чрез хеш функция, за която се преструваме, че върна стойност 10. След като подателят има хеш на съобщението, той може да създаде цифровия подпис, като приложи личния си ключ към хеш стойността със следната формула:

m (° С) = ° Сд моден н

Това всъщност е формулата за дешифриране на данни, които са шифровани с публичния ключ на получателя, но също така се използват за цифрово подписване на документи.

Що се отнася до цифровите подписи:

• Стойността на m (° С) ще бъде подписът.
• Стойността на ° С е хешът на съобщението (10).
• Стойността на д е част от личния ключ на изпращача, който получихме по-рано (29).
• Най- моден функция е същата операция на остатъка, която покрихме по-рано.
• Стойността на н е другата част от личния ключ на изпращача, която изчислихме в началото (221).

Така че, нека да включим всичко това в нашата формула:

m (° С) = 1029 мод 221

    m (° С) = 100 000 000 000 000 000 000 000 000 мод 221

Нека да стартираме това чрез следния модул калкулатор (обяснихме как работят тези операции в Измисляне на публичния ключ раздел). За да работи правилно, трябва да настроим своите входни данни като:

• номер а Тип – десетичен
• номер а стойност – 100000000000000000000000000000
• номер б Тип – десетичен
• номер б стойност – 221
• Уравнение на изчисление (това е само кодът, който казва на калкулатора коя операция да извърши. Този и други кодове могат да бъдат намерени на уеб страницата, свързана над секцията за въвеждане) – МО (А, В)

Ако сте направили нещата правилно, трябва да изглежда така:

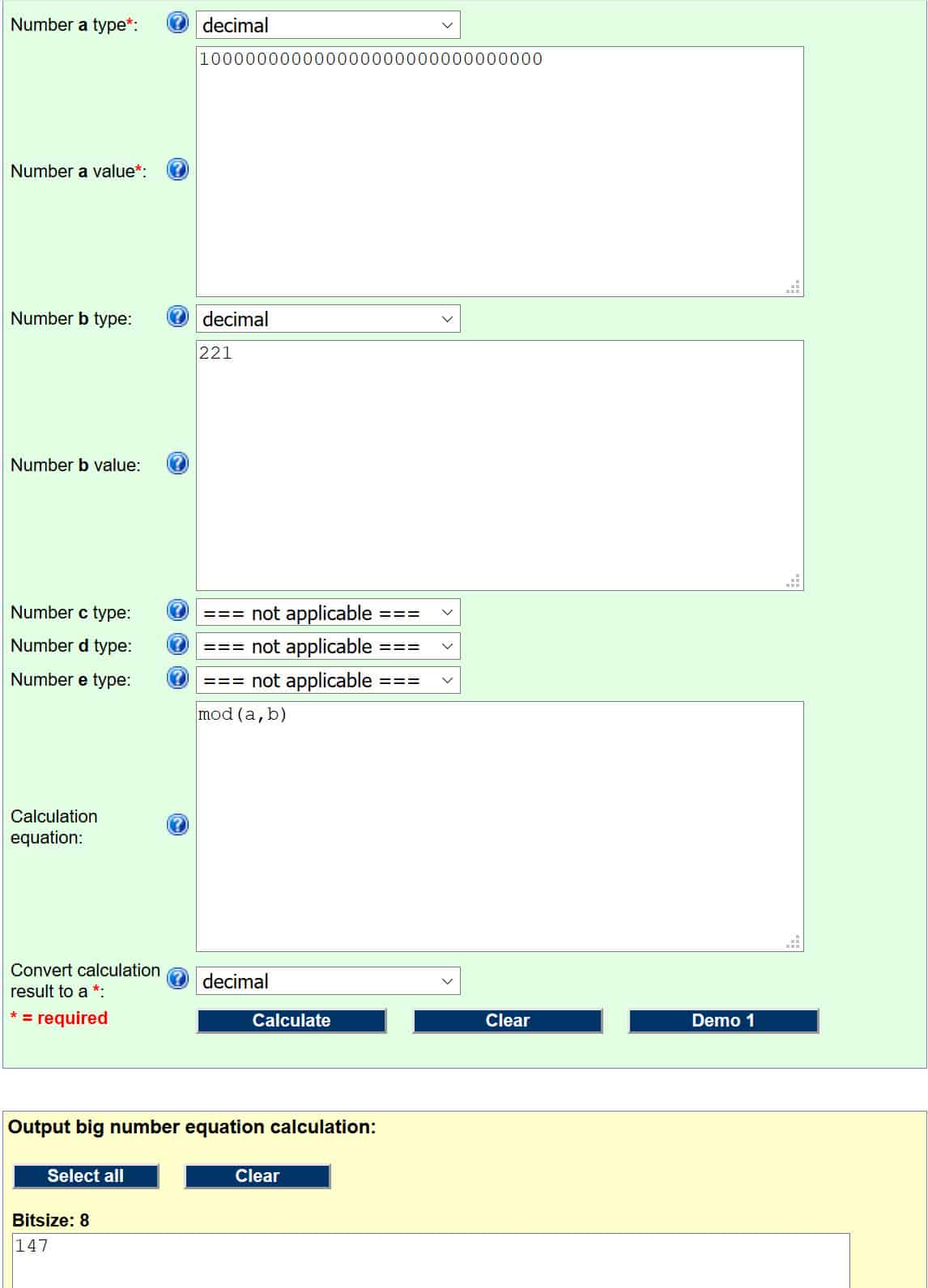
Номерът в жълтото поле е наш отговор, така че цифровият подпис за хеш на съобщението е 147.

За да докаже автентичността и целостта на съобщението, заедно с предоставяне на неотхвърляне, нашият изпращач ще предаде съобщението „Горещо е днес”Заедно с цифровия подпис на 147 на желания от тях получател. Само не забравяйте, че използвахме малка стойност за хеша, за да опростим нещата, вместо реалния хеш на съобщението.

Проверка на цифрови подписи

Цифровите подписи са полезни само ако можем да проверим дали са законни. Докато личният ключ на подателя не е компрометиран, получателят може да провери дали съобщението е автентично и запазва личната си цялост, като приложи следната формула към цифровия подпис:

    см) = mд моден н

При обръщане на процеса на подписване, това всъщност е формулата, която се използва за криптиране на данни в RSA. Когато използваме тази формула за проверка на подписите:

• Стойността на см) ще бъде хеш-стойността на изпращача в момента, в който са го подписали (поради структурата на алгоритъма на публичния ключ на RSA, прилагането на публичния ключ на изпращача чрез тази формула ще отмени операцията за подписване, която току-що извършихме, оставяйки ни с оригиналния си хеш за преструване ).
• Стойността на m е цифровият подпис (147).
• Стойността на д е част от публичния ключ на подателя, който получихме по-рано (5).
• Най- моден функция е същата операция на остатъка, която покрихме по-рано.
• Стойността на н е другата част от публичния ключ на изпращача, която изчислихме в началото (221).

Нека го хвърлим във формулата:

    см) = 1475 мод 221

    см) = 68,641,485,507 мод 221

Нека използваме същия модул калкулатор като преди и да поддържаме всичко същото, освен:

• номер а стойност – 68641485507

Ако сте въвели нещата правилно, трябва да получите резултат от:

см) = 10

Сега, след като получателят е изчислил хеш стойността от цифровия подпис, следващата им стъпка е да изчисли хеш стойността на съобщението, което е получил, “Горещо е днес“. Ако си спомняте от по-рано, всъщност не използвахме истинския хеш на SHA-256 на съобщението, защото номерът щеше да е твърде голям и да направи примера твърде сложен.

Вместо това ние се преструвахме, че хеш функцията всъщност ни даде малкия брой, 10, за нашия принос. Тъй като хеш функциите винаги извеждат един и същ резултат за даден вход, когато нашият получател поставя „Горещо е днес“Чрез нашата въображаема хеш функция те също биха получили стойността на 10.

Процесът на проверка на подписа води до две стойности. Първата стойност е хешът, какъвто е бил, когато подателят го цифрово подписва с личния си ключ. Изчислихме това по-горе с помощта на публичния ключ на изпращача.

Втората стойност е хешът на съобщението, което получателят е получил. Това се изчислява, като се използва същата хеш функция, която изпращачът използва за хеширане на първоначалното си съобщение. След това тези две стойности се сравняват и ако стойностите са едни и същи, тогава можем да приемем, че съобщението е автентично, запазва целостта си и че не може да бъде повторяемо. Разбира се, това предполага, че личният ключ на изпращача не е бил компрометиран.

Тъй като нашият пример върна стойност на 10 за хеша, когато той е бил подписан от изпращача, както и стойност на 10 като хеш на съобщението, което е получено, можем да приемем, че съобщението, „Горещо е днес” идва от лицето, което твърди, че го е изпратило, и че не е променено откакто е изпратено.

Ако получателят иска да отговори, за да може техният кореспондент да потвърди съобщението им по същия начин, целият процес се повтаря, с изключение на това, че личните и публичните ключове на получателя се използват съответно за процесите на подписване и потвърждаване.

Цялата тази математика може да ви е отклонила цялата идея за цифрови подписи. Не се притеснявайте, защото внедряването на RSA автоматизира този процес, така че не е нужно да разбивате никакви числа.

Плюсове RSA & минуси

RSA е един от най-широко поддържаните и прилагани алгоритми за цифров подпис, въпреки че има ход към по-новите, по-ефективни и сигурни алгоритми като ECDSA и EdDSA.

В сравнение с DSA (който ще разгледаме в следващия раздел), RSA е по-бърз при проверката на подписите, но по-бавен при генерирането им. Тъй като подписите обикновено се създават веднъж и се проверяват многократно, RSA обикновено се предпочита пред DSA.

DSA

Сигурността на алгоритъма на цифровия подпис се основава на две математически концепции, дискретен проблем с логаритъм и някои свойства на модулната експозиция. За някои групи е невъзможно да се изчислят техните дискретни логаритми със съвременни техники и технологии.

DSA генерация на ключове

За да генерирате DSA ключове, първата стъпка е да изберете параметрите, които група потребители в една и съща система могат да използват за генериране на двойка ключове.

Генериране на параметрите

• Избор на a хеш функция – SHA-256 е най-често срещаният вариант за изпълнение на съвременните изисквания за сигурност.
• Разрешаване на дължината на ключовете, L и н – Тези дни, L трябва да бъде поне 2,048 бита, докато н трябва да е поне 256 бита.
• Решете премиер, р, това е същата дължина като н.
• Изберете премиер, р, където р-1 е кратно на р.
• Изберете номер, г, използвайки следната формула (където з е произволно число между 1 и р-1):

г = з(р – 1) /р моден р

Обикновено тези стойности са много големи числа, за да се направи алгоритъмът сигурен. За да запазим нашия пример от твърде трудно да се изчисли или обясни, ще използваме много по-малки числа, които всъщност не биха били сигурни. Нека да кажем, че:

    р = 5

    р = 11

Да намеря г, ние включваме своите числа във формулата. Ще използваме 3 като нашата стойност за з:

г = 3 (11-1) / 5 мода 11

г = 32 мод 11

г = 9 мод 11

Ще използваме същия модул калкулатор като в Как личният ключ на изпращача се използва за цифрово подписване на хеш стойността секция. Параметрите ще бъдат същите, с изключение на:

• номер а стойност – 9
• номер б стойност – 11

Ако сте въвели всичко правилно, това ще ви даде резултат за г на 9.

Генериране на потребителските ключове

След това отделните потребители вземат тези параметри и ги използват, за да формират своята ключова двойка:

• Частният ключ (х) е число между тях 0 и р, които зададохме на 5. За нашия пример ще изберем 2 да бъде х, нашият частен ключ.
• Публичният ключ (ш) се изчислява по следната формула:

    ш = гх моден р

Следователно:

ш = 92 мод 11

ш = 81 мод 11

Ще използваме един и същ модул калкулатор още веднъж. Параметрите ще бъдат същите, с изключение на:

• номер а стойност – 81
• номер б стойност – 11

Ако сте въвели нещата правилно, би трябвало да получите резултат от y = 4. Следователно публичният ключ е 4.

Сега, когато генерирахме всички наши ценности, нека ви дадем бърз резюме. Параметрите за системата са:

• р = 11
• р = 5
• г = 9

Нашата ключова двойка е съставена от:

• Частният ключ, х = 2
• Публичният ключ, ш = 4

Цифрово подписване на данни с DSA

Изпращачите могат да използват личния си ключ DSA за цифрово подписване на данни, което позволява на получателя им да провери дали съобщението е автентично и запазва своята цялост. Освен това не позволява на изпращача да може да отхвърли съобщението.

Процесът на подписване започва с генериране на произволна стойност к, което е между 1 и р. За този пример, нека просто изберем 3 като наше „случайно“ число, к.

След това следваме следната формула, за да създадем индивидуален ключ (R) за съобщението:

R = (гк моден р) mod q

Нека се хвърлим в нашите номера:

R = (93 мод 11) мод 5

R = (729 мод 11) мод 5

Използваме отново нашия модулен калкулатор, влизайки 729 и 11, което ни дава резултат от 3. Следователно:

R = 3 мод 5

И след това отново повтаряме модулната операция с новите стойности, за да ни даде:

R = 3

Нашата стойност за R се използва като ключ за съобщението.

Излизаме с другата част на цифровия подпис, с, със следната формула:

с = к-1(Н(m) + XR) мод р

Най- к-1 не представлява отнемане на отрицателната сила на к, но вместо това да изчислим модулния обрат, точно както в нашия Измисляне на подсекция на частния ключ в по-ранната част на статията, където говорихме за RSA.

Н(m) е хеш стойността за съобщението, което изпращащият подписва. Обикновено това ще бъде дълга хеш стойност, получена от съобщението, точно както в Разбиране на хеш стойностите подраздел по-горе, който покрихме, когато говорихме за алгоритъма на RSA.

За този пример ще запазим нещата прости. Точно както в раздела за RSA, ние ще кажем, че нашето послание, m, е „Горещо е днес“ и че хешът на съобщението Н(m), е 10.

Затова нека въведем всички наши стойности във формулата:

с = 3-1 (10 + 2 х 3) (мод 5)

с = 3-1 (10 + 6) (мод 5)

с = 3-1 (16) (мод 5)

Сега, ние вземаме модулния обрат на 3 за реда на 5 (тъй като 5 е нашата стойност за р), използвайки същия модулен обратен калкулатор от по-рано. Въведете 3 като цяло число и 5 като модула, който ще ви даде резултат от 2. Следователно:

с = 2 (16) (мод 5)

с = 32 (мод 5)

Да се ​​върнем към нашия калкулатор за нормалната работа по модул, като запазваме същите параметри, които използвахме по-рано, освен:

• номер а стойност – 32
• номер б стойност – 5

Ако сте направили това правилно, той ще даде стойност за с от 2. Цифровият подпис е съставен от R и с (3 и 2 съответно). Изпращачите предава цифровия подпис на получателя си заедно със своето съобщение, “Горещо е днес“. Те също ще споделят стойностите на p, q, г и ш с получателя им.

Проверка на цифрови подписи

Когато получателят получи цифровия подпис заедно със съобщението, той може да провери целостта и автентичността на съобщението със следния набор от изчисления.

Първата стъпка е да намерите хеш на съобщението, което са получили. Получателят прави това, като пуска цялото съобщение чрез хеш функция. За да поддържате нещата прости и последователни, нека кажем, че хешът на съобщението, Н(m) е 10.

На получателя са изпратени и следните стойности, които те използват в процеса на проверка:

• Цифровият подпис (r, s) – 3, 2
• п – 1
• q – 5
• g – 9
• у – 4

Първото изчисление е да се намери w:

w = с-1 мод р

Отново с-1 представлява поемане на модулния обрат. Нека въведем нашите стойности:

w = 2-1 мод 5

Ще използваме модулния обратен калкулатор от по-рано. Въведете 2 като цяло число и 5 като модула, който ще ви даде резултат от 3 за w. Следващата стъпка е да намерите ф1 със следната формула:

ф1 = Н(m) х w моден р

Нека да хвърлим нашите ценности:

ф1 = 10 х 3 мод 5

ф1 = 30 мод 5

Обратно към нормалния модул калкулатор, като запазваме същите параметри, които използвахме по-рано, с изключение на:

• номер а стойност – 30
• номер б стойност – 5

Това ни дава резултат от 0 за ф1.

Използваме следващата формула, за да измислим ф2:

ф2 = R х w моден р

Нека въведем нашите номера:

ф2 = 3 x 3 mod 5

ф2 = 9 мод 5

След това се връщаме към нормалния модул калкулатор, използвайки същите параметри като по-рано, с изключение на:

• номер а стойност – 9
• номер б стойност – 5

Ако въведете това правилно, това ще ви даде резултат за ф2 от 4.

Сега, когато имаме своите ценности за ф1 и ф2, можем да намерим V, със следната формула:

v = (гu1шu2 моден р) мод р

Нека се хвърлим в нашите номера:

V = (90 x 44 mod 11) мод 5

V = (1 х 256 мод 11) мод 5

V = (256 mod 11) мод 5

Връщаме се към нашия нормален модул калкулатор, използвайки същите параметри като по-рано, с изключение на:

• номер а стойност – 256
• номер б стойност – 11

Това ни дава резултат от 3. Следователно:

V = 3 мод 5

След това използваме нормалния модул калкулатор един последен път, отново със същите параметри, с изключение на:

• номер а стойност – 256
• номер б стойност – 11

Това ни дава резултат за V от 3.

Ако съобщението е автентично и не е било подправено, тогава v ще бъде равно на r:

    v = 3

    r = 3

    3 = 3

Следователно съобщението е изпратено от собственика на частния ключ и съобщението не е променено от момента на подписването му.

Професионални DSA & минуси

Сигурността на DSA зависи от това дали използва адекватни номера. В допълнение на p, q и г спазвайки правилните параметри, стойността на к също трябва да е случайно. Тя не трябва да бъде предсказуема стойност или стойност, която се използва многократно. Ако тези изисквания не са изпълнени, ключът може да бъде възстановен от нападател.

Въпреки тази възможност, DSA обикновено се счита за сигурен, стига да е изпълнен правилно и да използва адекватни стойности. Въпреки че е сравнително сигурен, DSA няма тенденция да се прилага много в сравнение с RSA или другите методи за цифров подпис. В сравнение с RSA, той може да генерира ключове по-бързо и също така е по-бърз при генериране на цифрови подписи, но по-бавен при проверката им.

Версия 7.0 на OpenSSH по подразбиране спря да поддържа клавиши DSA, което изглежда е знак, че светът се движи покрай DSA и към други алгоритми.

ECDSA & EdDSA

RSA и DSA не са единствените алгоритми за цифров подпис, нито са най-подходящи за всички ситуации. Има редица други, като напр ECDSA и EdDSA, които имат свойства, които ги правят за предпочитане при определени обстоятелства.

За съжаление, те разчитат на още по-сложна математика, като например елиптична крива и криптография на кривата на Едуардс. Днес няма да ги обхващаме подробно поради тази допълнителна сложност, но ще говорим за някои от техните потенциални позитиви и негативи.

ECDSA

Алгоритъмът за цифров подпис на елиптичната крива е вариант на DSA, който включва криптография на елиптична крива. Той осигурява подобно ниво на сигурност като RSA, но с много по-малък ключ. Това го прави по-ефективен от RSA или DSA в повечето аспекти на работата.

EdDSA

Това е друга алтернатива на DSA, само че тя се основава на криви на Twisted Edwards. Той е сравнително нов, що се отнася до алгоритмите, което има както своите предимства, така и недостатъци. От положителна страна, той използва по-нови техники, които допринасят за неговата ефективност.

За съжаление, по-новите алгоритми не са били изложени на толкова голям контрол, така че много хора са предпазливи, когато решават дали да ги прилагат или не..

Въпреки това, използването на EdDSA осигурява високо ниво на производителност, устойчивост на атаки на странични канали и премахва необходимостта от уникално произволно число във всеки подпис. На този етап EdDSA изглежда обещаващо и започва да вижда по-широко приложение, но ще трябва да изчакаме и да видим дали бъдещите проучвания откриват дупки в сигурността.

Цифрови сертификати

Всеки може лесно да направи двойка ключове, дори и нападател. И така, това, което пречи на някого да направи куп ключове и да се преструва, че е президент, или да позира като всеки друг?

Е, нищо не пречи на някого да твърди, че е друг човек, но има система, която позволява на другите да проверят дали човекът наистина е този, за когото се твърди, че е. Нарича се инфраструктура за публични ключове (PKI), и включва цифрови сертификати, които свързват публичния ключ на физическо лице или образувание с тяхната истинска идентичност. Тези сертификати са подписани от други, за да посочат колко точно трябва да се вярва на сертификата.

Можете да сравните процеса с използването на нотариуси за проверка на документи. Ако някой има копие на акт за раждане, може да се поставите скептично дали това е законно или не. Ако същото свидетелство за раждане беше подписано и подпечатано от нотариус, много по-вероятно е да повярвате, че това е истинско копие.

Защо?

Тъй като подписът и печатът показват, че доверено публично образувание е видяло физическото лице и оригиналния му акт за раждане, след това се проверява дали копието в действителност е законно. Нотариусът заверява копието на акта за раждане и залага на тяхната репутация зад него със своя подпис и печат.

Доверието, което имаме към нотариуса, се прехвърля в копието на акта за раждане, което ни позволява да му се доверяваме много повече от това, което не е нотариално заверено..

Има два основни типа сертификация, cудостоверяващи власти (CA) и мрежата на доверие.

Сертифициращи органи

Сертифициращите органи са надеждни организации, които извършват проверки на физически или юридически лица, за да проверят дали те са законният собственик на публичен ключ. Ако проверките разкрият, че физическото лице е истинският собственик, тогава сертифициращият орган подписва сертификата със собствен ключ, което означава, че е приключил проверката и счита, че индивидуалният и публичният ключ са законно свързани.

Докато се доверяваме на сертифициращия орган и процеса на проверка на ключа, тогава можем да се доверим на сертификат, който е подписан от тях, и по този начин публичният ключ наистина представлява този индивид.

В зависимост от вида на сертификата и неговото приложение различните нива могат да имат различни процеси на проверка и по този начин или представляват по-висока или по-ниска степен на доверие.

Мрежата на доверие

Мрежата на доверие работи при подобно предположение, с изключение на tтук няма централни органи като сертификационни органи, които извършват процеса на проверка и подписват сертификатите.

Вместо това мрежата на доверие разчита на други лица да подписват сертификати, залагайки на репутацията си на връзката между индивида и публичния ключ. Тази система се използва най-вече с PGP, където потребителите лесно могат да правят свои собствени сертификати.

Работи така:

Да речем, че имате двама приятели, които искат техните сертификати да бъдат подписани, за да докажат, че са законните собственици на съответните им публични ключове. Познавате добре тези хора и ви показват техните държавни документи за самоличност, което ви прави абсолютно сигурни, че те са тези, за които казват, че са, и по този начин са истинските собственици на публичните ключове, за които претендират..

Тъй като знаете, че те са законните собственици на техните публични ключове, с удоволствие използвате личния си ключ, за да подпишете техните сертификати, като залагате на тяхната репутация и по същество казвате „Да, проверих самоличността на тези лица и те са кои те твърдят, че са ”. Тези двама приятели могат да направят същото и на вас.

Нека да кажем, че всеки от двамата ви приятели има още двама приятели, които искат да бъдат подписани сертификатите им. Ако вашите двама приятели подпишат тези други сертификати, тогава можете да използвате доверието, което имате във вашите приятели, за да приемете, че тези други хора са наистина тези, за които казват, че са и.

След това приятелите на вашите приятели могат да подпишат сертификатите на хората, на които имат доверие и така нататък, в крайна сметка да изградят голяма мрежа от хора, на които имат доверие. След като тези мрежи станат достатъчно големи и станат взаимосвързани с други мрежи, те могат да бъдат използвани като средство за доверие на всеки друг в мрежата.

Колкото повече подписи са в сертификат, особено ако става въпрос за подписи от високодоверни лица, толкова повече можете да се доверите на нечий цифров сертификат и връзката между техния публичен ключ и тяхната самоличност.

Потребителите на PGP често провеждат ключови партита за подписване, където хората се събират, за да проверят самоличността си и своите цифрови сертификати. Тези събирания помагат за привличането на нови хора в мрежата.

Въпреки че идва с някои сложности, предимството на мрежата от доверие на системата е, че няма централен орган, който може да се повреди.

Безопасни ли са цифровите подписи?

В общ смисъл, цифровите подписи са сигурни, освен ако не е компрометиран личният ключ на получателя. Ако собственикът е уведомил друго лице, е оставил записания частен ключ или го е откраднал по друг начин, тогава е възможно нападателят да подписва цифрово съобщения, сякаш те са собственикът.

Това може да доведе до нападателят, представящ се за жертвата си или подправяне на техните данни. Това е огромен проблем със сигурността и всеки, който подозира, че ключът им е компрометиран, трябва да отнеме цифровия си сертификат, който ги свързва с техния публичен ключ, и да издаде нов.

Има няколко други предупреждения, що се отнася до сигурността на цифровия подпис. Трябва да се използва подходящ алгоритъм за цифров подпис, който също трябва да бъде приложен правилно. Наред с това трябва да има и начин за свързване на публичния ключ със собственика му, обикновено чрез цифрови сертификати.

Докато тези изисквания са изпълнени, вие следвате най-добрите практики в индустрията и тогава вашият личен ключ не е компрометиран цифровите подписи са отличен начин за осигуряване на автентичност, цялостност и неотблъскване на данните.

Структурирани данни от Kai Stachowiak, лицензиран под CC0