امضاهای دیجیتال چیست و چگونه کار می کنند؟

امضاهای دیجیتال نوعی نسخه های الکترونیکی مانند امضاهای دست نویس شما هستند. آنها به افراد اجازه می دهند بررسی کنند صحت و تمامیت داده ها, و همچنین از جلوگیری از امضاءكنندگان امكان انكار (انكار) درگیری آنها جلوگیری می كند.

این ویژگی ها منجر به پذیرش امضاهای دیجیتالی در طیف گسترده ای از برنامه ها از جمله بسیاری از پروتکل های امنیتی ما ، ایمیل ایمن و در مدیریت حقوق دیجیتال شده است..

در این مقاله ، به بحث خواهیم پرداخت امضاهای دیجیتال چیست, در جایی که از آنها استفاده می شود و همچنین جزئیات فنی دو الگوریتم محبوب ترین, RSA و DSA.

امضاهای دیجیتالی چیست?

همانطور که گفته شد ، امضاهای دیجیتال سه خاصیت بسیار مهم را در اختیار ما قرار می دهند. اینها احراز هویت ، صداقت و عدم رد است.

احراز هویت این فرایند تأیید این است که فردی که پیامی را ارسال می کند واقعاً همان کسی است که می گوید آنها هستند و نه یک شخص متهم کننده.

تمامیت داده ها یا پیام به این واقعیت اشاره دارد که آیا در همان حالت ارسال شده در هنگام ارسال رسیده است یا خیر. اگر پیامی تغییر یافته یا دستکاری شده باشد ، دیگر صداقت خود را حفظ نمی کند.

اگر داده یا پیام است غیر قابل انکار, این بدان معنی است که نویسنده آن نمی تواند بحث کند که آنها خالق واقعی این سند بودند. این ویژگی قابل قبول بودن را از بین می برد ، یا بهانه قدیمی “ببخشید ، دوست من از حساب من استفاده کرده است”.

تا زمانی که کلید خصوصی فرد به خطر نیفتد ، امضاهای دیجیتالی می توانند هر سه ویژگی را به داده ها ارائه دهند.

شاید تعجب کنید که چرا در وهله اول به این خصوصیات احتیاج داریم. بیایید یک قدم عقب برداریم و در مورد نحوه انجام کارها در مواجهه چهره به چهره فکر کنیم.

بیایید بگوییم که شما به دوست خود مایک 100 دلار مدیون هستید. شما آدم خوبی هستید ، بنابراین خوشحال می شوید وقتی پول دریافت می کنید به او بازپرداخت کنید.

بهترین راه برای انجام این کار فقط دادن یک لایحه 100 دلار به مایک است. شما سالهاست که او را می شناسید و می دانید که چگونه به نظر می رسد ، بنابراین چنین خواهد بود تأیید هویت وی آسان است و بنابراین تأیید می کنید که پول را به شخص مناسب می دهید.

اگر واقعاً مقعد بودید ، حتی می توانید شناسنامه وی را بررسی کنید و از وی بخواهید که یک دست نوشته برای شما امضا کند. امضاي دريافت ، آن را به يكپارچگي مي بخشد و آن را قابل رد شدن مي داند.

چه می شود اگر به جای انجام معامله رو در رو ، با کسی تماس گرفتید که بگوید آنها مایک هستند و باید 100 دلار برای شماره حساب 12345678 بفرستید.

شما می گویید: “اما شما مثل مایک به نظر نمی رسید.”.

“من سرما خورده ام. اکنون ارسال کنید ، من به پول احتیاج دارم. “

آیا می خواهید پول ارسال کنید؟ احتمالا نه.

هیچ راهی برای دانستن اینکه آیا این واقعاً مایک است یا شماره حساب صحیح نیست. برای همه شما می دانید ، این می تواند یک متهم باشد که سعی در سرقت از شما داشته باشد. به جای انتقال سریع پول ، بهتر است صبر کنید تا مایک را مشاهده کنید تا بتوانید پول را به صورت حضوری به او بدهید.

دقیقاً مانند سناریوی فوق ، ما اغلب در شرایطی قرار می گیریم که لازم باشد هویت یک مهمانی یا تمامیت داده ها در دنیای آنلاین را تأیید کنید. به همین دلیل امضاهای دیجیتال به عنوان مکانیزمی که بتواند این خصوصیات را فراهم کرده و معاملات آنلاین ایمن را تسهیل کند ، افزایش یافته است.

بدون آنها ، ما نمی دانیم با چه کسی صحبت می کنیم ، نمی توانیم مطمئن باشیم که داده ها با آنها دستکاری شده است یا نه ، و شخص می تواند انکار کند که آنها مسئول بوده اند.

استفاده از امضاهای دیجیتال

این خصوصیات امضاهای دیجیتال باعث می شود تا آنها در طیف گسترده ای از کاربردها مفید باشند. آنها غالباً توسط خودشان یا درمورد رمزگذاری در طیف وسیعی از پروتکلهای امنیتی مختلف ، مانند:

• IPsec
• SSH
• TLS

آنها همچنین اغلب استفاده می شود مدیریت حقوق دیجیتال, که در فناوری blockchain, که در مدیریت قرارداد برنامه ها ، به عنوان بخشی از توزیع نرم افزار, و در دارایی، مالیه، سرمایه گذاری.

تاریخچه امضاهای دیجیتال

ایده امضاهای دیجیتالی اولین بار توسط رمزنگاران مشهور ویتفیلد دیفی و مارتین هلمن در مقاله 1976 خود منتشر شد مسیرهای جدید در رمزنگاری. در سال 1978 ، رونالد ریوست ، ادی شمر و لن آدلمن الگوریتم RSA را در معرض دید عموم قرار دادند که می تواند برای تولید امضای دیجیتالی ناامن مورد استفاده قرار گیرد.

یک دهه دیگر طول کشید تا امضاهای دیجیتالی در یک برنامه گسترده پدیدار شوند: انتشار Lotus Notes 1.0 IBM. از آن زمان به بعد ، با ظهور تکنیک های جدید ، امضاهای دیجیتالی شروع به پذیرش گسترده تر کردند و لزوم احراز هویت آنلاین و بررسی صداقت افزایش یافت..

معرفی مختصر به رمزنگاری کلید عمومی

قبل از پرش به امضاهای دیجیتال ، بهتر است برخی از جنبه های مهم رمزنگاری کلید عمومی را پوشش دهیم, که اساس کار امضاهای دیجیتال را تشکیل می دهد.

اگر نسبت به رمزنگاری نسبتاً جدید باشید ، سیستمی که با آن بیشتر آشنا خواهید شد رمزگذاری کلید متقارن است. این فقط بدان معنی است که برای رمزگذاری و رمزگشایی داده ها از همان کلید (که شبیه به یک رمز عبور است اما تفاوت هایی با آن دارد).

رمزگذاری کلید عمومی یک انقلاب بود ، زیرا این امر درگیر بود استفاده از کلیدهای جداگانه برای فرآیند رمزگذاری و رمزگشایی, منجر به طیف وسیعی از برنامه های رمزنگاری مختلف. این دو کلید یک جفت کلیدی را تشکیل داده اند که از کلید عمومی و کلید خصوصی تشکیل شده است. بدیهی است که کلید عمومی می تواند به صورت عمومی تقسیم شود ، در حالی که باید کلید خصوصی مخفی نگه داشته شود تا سیستم ایمن باشد.

دو مورد متداول از رمزنگاری کلید عمومی عبارتند از رمزگذاری و امضاهای دیجیتالی.

رمزگذاری

یکی از ویژگیهای مهم رمزنگاری کلید عمومی این بود این اجازه می دهد تا طرفهایی که هرگز ملاقات نکرده اند به صورت محرمانه پیام های دیگری را ارسال کنند. فرستنده کلید عمومی گیرنده مورد نظر خود را جستجو می کند (این موارد را می توان در سرورهای کلید عمومی ، در وب سایت های شخصی یا به سادگی با پرسیدن فرد مشاهده کرد) ، سپس قبل از ارسال آن به گیرنده ، پیامی را با این کلید رمزگذاری می کند..

گیرنده تنها شخصی است که می تواند به پیام دسترسی پیدا کند – با فرض اینکه کلید خصوصی به خطر نیفتد – با رمزگشایی آن با کلید خصوصی آنها. حتی اگر از کلید عمومی برای رمزگذاری پیام استفاده شده باشد ، فقط با کلید خصوصی قابل رمزگشایی است. اگر گیرنده بخواهد پاسخ دهد ، کلید عمومی فرستنده اصلی را پیدا می کند ، سپس فرایند را تکرار کنید.

همچنین ببینید: انواع رمزنگاری رایج توضیح داده شده است

چگونه امضاهای دیجیتال کار می کنند?

همانطور که گفتیم ، از امضاهای دیجیتال برای تأیید اعتبار استفاده می شود ، برای دیدن اینکه آیا داده ها با چه مواردی دستکاری شده است ، و همچنین برای عدم رد کردن استفاده می شود. طیف وسیعی از مکانیسم های مختلف وجود دارد که می تواند برای امضاهای دیجیتالی مورد استفاده قرار گیرد ، و هر یک در نحوه ساخت آنها تغییرات جزئی دارند..

به طور کلی ، این الگوریتم ها باید از سه الگوریتم فرعی تشکیل شوند:

• الگوریتم تولید کلید – این الگوریتم یک جفت کلید تصادفی برای کاربر ایجاد می کند. اعداد درگیر شده در جفت اصلی باید پارامترهای خاصی را رعایت کنند تا امنیت در نظر گرفته شوند. دو مورد از مهمترین جنبه ها این است که اعداد به اندازه کافی تصادفی و اندازه کافی هستند.
• الگوریتمی برای امضای داده ها – هنگامی که یک کاربر کلیدهای خود را پیدا کرد ، روشهای خاصی برای نحوه استفاده از داده ها در فرآیند امضا وجود دارد.
• الگوریتمی برای تأیید امضا – به همین ترتیب ، تأیید یک امضا به دنبال یک روند از پیش تعیین شده است.

برای اینکه سیستم امضای دیجیتالی مؤثر باشد ، باید به گونه ای ساخته شود که:

• داده هایی که با یک کلید خصوصی امضا شده اند تأیید شده است با کلید عمومی عمومی یکسان.
• لازم است جعل امضای معتبر بدون دانستن کلید خصوصی فرد غیرممکن باشد (با استفاده از فناوری و تکنیک های فعلی).

برخی از رایج ترین طرح های امضای دیجیتال شامل RSA ، DSA ، EcDSA و EdDSA هستند.

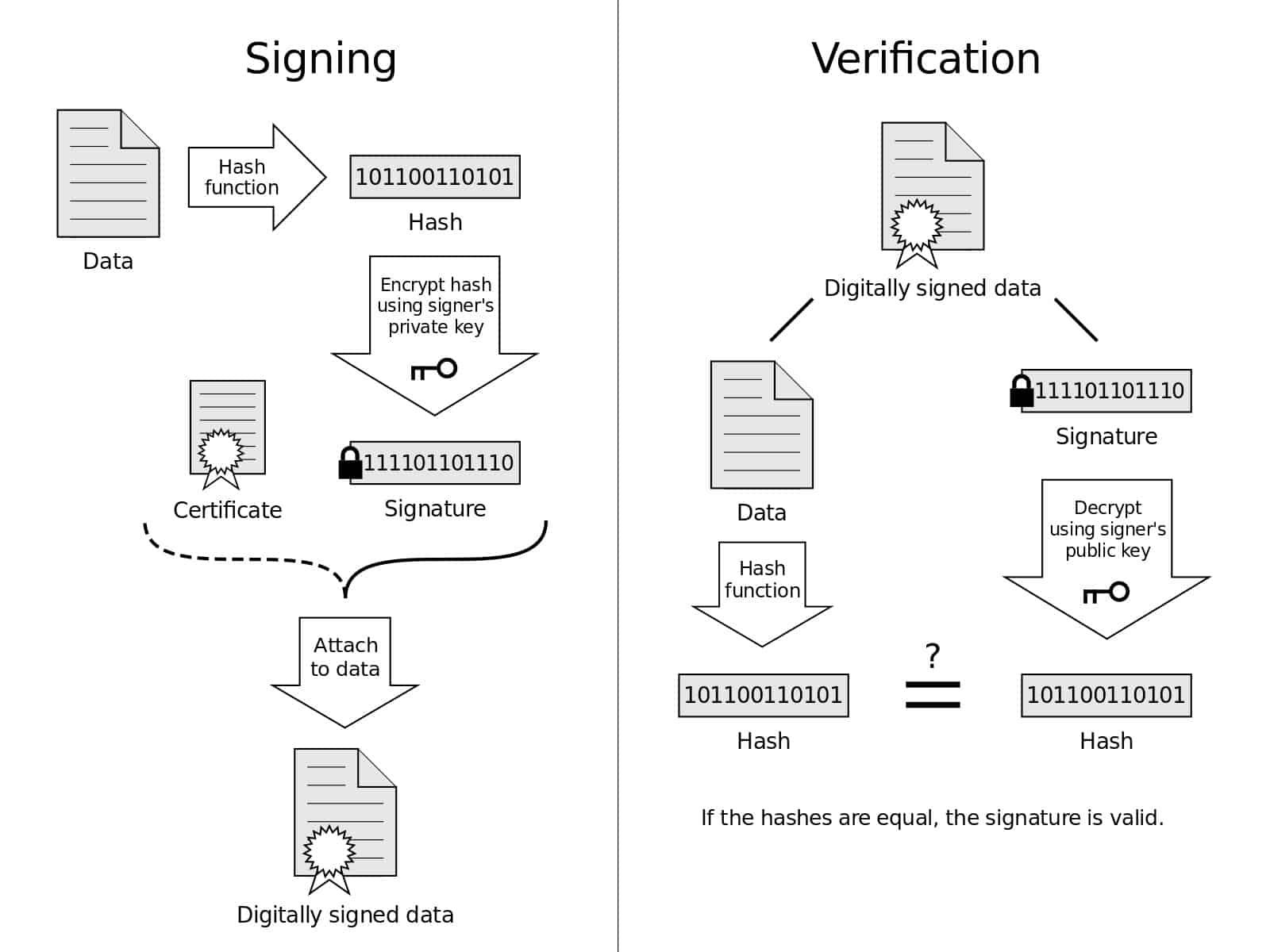
این تصویر نمایانگر بصری فرآیندهای امضای و تأیید است. نمودار امضای دیجیتال توسط Acdx تحت مجوز CC0

RSA

RSA اولین الگوریتم امضای دیجیتال بود ، اما می تواند از آن برای رمزگذاری کلید عمومی نیز استفاده شود. در این مقاله از جنبه رمزنگاری خواهیم گذشت ، اما می توانید در مقاله جامع ما که اطلاعات مربوط به عملکرد RSA و چگونگی عملکرد آن است ، اطلاعات بیشتری در مورد آن کسب کنید..

تولید کلید RSA

در پیاده سازی های ایمن RSA ، جفت های کلیدی به طور خودکار تحت فرآیند زیر ایجاد می شوند:

نسل اول

دو شماره اصلی اصلی انتخاب می شوند, پ و ق. اندازه دقیق این ابتکارات بسته به اندازه کلید متفاوت خواهد بود. این روزها ، حداقل کلیدهای RSA 2048 بیتی معمولاً برای امنیت کافی توصیه می شوند ، بنابراین ما در مورد دو شماره اصلی صحبت می کنیم که برای تولید یک عدد 2048 بیتی ضرب می شوند..

2048 بیت اندازه ای در سیستم شماره دودویی است. اگر تعدادی از این اندازه به سیستم اعشاری شناخته شده ما تبدیل شود ، تقریباً به طول طولانی می رسد:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

مقدمات ابتدایی در RSA باید بصورت تصادفی انتخاب شده و دارای طول های مشابه باشند.

در مثال ما ، از اعداد بسیار کمتری استفاده خواهیم کرد تا درک چیزها آسانتر شود. توجه داشته باشید که استفاده از کلیدهای این اندازه باعث می شود امضاهای دیجیتال برای جعلی بودن بی اهمیت باشند. به همین دلیل است که چنین مقادیر بزرگی در عمل استفاده می شود.

بیایید بگوییم که:

پ = 13

ق = 17

اولین قدم برای محاسبه مدول خواهد بود ن با استفاده از فرمول زیر:

n = قطعه

ن = 13. 17

ن = 221

ارزش ن همچنین طول کلیدی است.

عملکرد کمتری Carmichael

اکنون که ارزش آن را داریم ن, قدم بعدی استفاده از تابع تواتر Carmichael است:

ل(ن) = سی سی (پ – 1, ق – 1)

چند نکته وجود دارد که باید آنها را بفهمید:

• ل(ن) به معنی مقدار کامنت Carmichael برای مقدار است ن
• سی سی نشان دهنده پایین ترین ضرب مشترک است. این کمترین تعداد مشترکی است که هر دو دارند p-1 و q-1 می تواند به تقسیم شود

بیایید ارقام خود را به معادله وصل کنیم:

ل(221) = سی سی (13 – 1 ، 17 – 1)

ل(221) = سی سی (12 ، 16)

اگر در ریاضی ذهنی خوب هستید ، شاید این موضوع را فهمیده باشید 48 پایین ترین ضرب مشترک هر دو است 12 و 16. دلیل این است که 48 کمترین عددی است که هر دو این عدد می توانند در آن جای بگیرند (12 4 4 = 48 ، 16 x 3 = 48). از این رو:

ل(221) = 48

با کلید عمومی همراه شوید

در RSA ، کلید عمومی از مقدار تشکیل شده است ن (که قبلاً محاسبه کرده ایم 221) و ه. از آنجا که کلید عمومی آزادانه به اشتراک گذاشته می شود ، مقدار برای ه لازم نیست راز باشد در واقع ، این اغلب در عمل 65،537 تعیین می شود ، زیرا تعداد بزرگتر روند رمزگذاری را کند می کند. در مثال ما قرار خواهیم داد ه به 5, فقط برای اینکه آن را به یک شماره کوچک و ساده تبدیل کنید تا با آن کار کنید.

بنابراین ، کلید عمومی برای این مثال از آن تشکیل شده است 221 و 5. ما خصوصیات چگونگی استفاده از کلید عمومی را در بخش های بعدی پوشش خواهیم داد.

کشف کلید خصوصی

همانطور که کلید عمومی ما از دو شماره تشکیل شده است ، کلید خصوصی ما نیز همینطور است. کلیدهای خصوصی از آنها تشکیل شده است د و ه. ما قبلاً ارزش آن را می دانیم ه (5), و می توانیم از فرمول زیر استفاده کنیم د:

د = 1 /ه مود ل(ن)

توجه داشته باشید که مود فقط نمادی از یک عمل ماژول است ، که به معنای عادی این است که شما باید بخش دیگری را پس از تقسیم سمت چپ به سمت راست پیدا کنید. به عنوان مثال:

17 مود 3 = 2

این امر به این دلیل است که 3 بار در 17 بار در مجموع 5 بار و باقیمانده 2 متناسب است.

مثال ما کمی متفاوت است. “1 /ه مود“بخش معادله ممکن است به شما بگوید تقسیم کنید 1 توسط ه, اما در واقع اینگونه نیست گیج کننده است ، اما این راهی برای نمایندگی است معکوس مدولار. این معادله در واقع به ما می گوید که معکوس مدولار را محاسبه کنیم ه و ل(ن).

معکوس ماژولار به طور معمول با استفاده از الگوریتم طولانی اقلیدسی استخراج می شود ، اما ما در این مقاله آن را پوشش نمی دهیم. در عوض ، ما فقط یک ماشین حساب آنلاین برای آسان تر کردن امور استفاده خواهیم کرد.

اکنون که این کار را از سر راه دریافت نکردیم ، بگذارید مقادیر خود را در فرمول وارد کنیم:

د = 1/5 mod 48

برای پیدا کردن د, تنها کاری که باید انجام دهیم این است که ارزش خود را وارد کنیم ه (5) به حسابگر آنلاین که در آن می گوید عدد صحیح, سپس ارزش ما برای ل(ن), که است 48, جایی که می گوید مدول.

این نتیجه ای را به ما می دهد 29 با توجه به ماشین حساب آنلاین. بنابراین ، کلید خصوصی ما از این موارد تشکیل می شود:

ه = 5

د = 29.

حال که هر دو کلید را ایجاد کردیم ، سوال بعدی این است که “با آنها چه کار می کنیم؟” خوب ، می توانیم از آنها برای رمزگذاری و رمزگشایی پیامها از طریق رمزنگاری کلید عمومی استفاده کنیم ، اما این مقاله در مورد امضاهای دیجیتالی است ، بنابراین ما روی آن تمرکز خواهیم کرد.

امضای دیجیتالی داده ها با RSA

بیایید بگوییم که شخصی می خواهد پیامی را به دوست خود ارسال کند ، اما می خواهد مطمئن شود که دوست می تواند صحت و صحت پیام را تأیید کند. آنها می توانند این کار را با استفاده از امضای دیجیتال RSA برای امضای پیام انجام دهند.

قدم اول این است که کل پیام را از طریق یک تابع هش اجرا کنید. این توابع یک طرفه هستند که همیشه همان ورودی را برای ورودی معین ارائه می دهند. عملکردهای هش امن برای معکوس کردن غیرممکن است ، بدین معنی که از خروجی برای تشخیص ورودی نمی توان استفاده کرد. همچنین غیر ممکن است که دو پیام جداگانه خروجی یکسان داشته باشند.

می توانید اطلاعات بیشتری در مورد توابع هش در این قسمت کسب کنید چه حسی دارد? بخش مقاله ما, رمزگذاری ، هشدار ، نمک زدن – تفاوت چیست?

بیایید بگوییم که ما می خواهیم پیام را به صورت دیجیتال امضا کنیم “امروز گرم است“به طوری که گیرنده ما بداند که آیا این پیام معتبر است یا نه و در صورت استفاده از آن دستکاری شده است. بنابراین ما اجرا خواهیم کرد “امروز گرم است“از طریق یک تابع هش.

درک توابع هش

این روزها متداول ترین عملکرد هش ایمن SHA-256 است. وقتی پیام خود را از طریق یک ماشین حساب آنلاین SHA-256 قرار می دهیم ، نتیجه ای مانند این به ما می دهد:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

این مثال برای ما چند مشکل ایجاد می کند. اولین مورد این است که یک عدد اعشاری مانند کسانی نیست که بیشتر مردم به آنها عادت کرده اند. شاید متوجه شده باشید که در این شماره حروف وجود دارد ، و آنها فقط به بالا می روند f. این یک سرنخ به ما می دهد که در واقع یک عدد شش ضلعی است.

سیستم hexadecimal به جای پایه 10 از پایه 16 متکی است, مانند سیستم عددی که معمولاً از آن استفاده می کنیم. این بدان معناست که به جای شمارش در ضرب 10 ، تعداد آن در تعداد 16 است و از 6 حرف اول الفبای ما برای تشکیل این اعداد اضافی استفاده می شود. عددی مانند این می تواند به سیستم اعشاری روزمره ما تبدیل شود ، اما این خارج از محدوده این مقاله نیست.

دومین مسئله ای که ما داریم این است که این تعداد واقعا بزرگ است. اگر به دهدهی تبدیل شود ، حتی طولانی تر می شود. از آنجا که ما در این راهنما به دنبال سادگی هستیم ، اجرای محاسبات با چنین تعداد زیادی باعث می شود تا مسائل برای ایجاد مفاهیم اساسی گیج شود..

با ایده نشان دادن چگونگی عملکرد امضاهای دیجیتال RSA به روشی که درک آن آسان باشد ، در مثال زیر ما از چنین ارزش هش بزرگی استفاده نمی کنیم. در عوض ، وانمود خواهیم کرد که مقدار هش “امروز گرم است“به سادگی است 10.

ما همچنین باید وانمود کنیم ، مانند هر هش واقعی ، هر زمان که وارد عملکرد “هش امروز” شویم ، همیشه ارزش 10. برای اینکه با نحوه عملکرد توابع هش مطابقت داشته باشیم ، باید تظاهر کنیم که هیچ ورودی دیگری نمی تواند همان ارزش را داشته باشد. به همین ترتیب ، ما باید وانمود کنیم که همچنین نمی توان ورودی اصلی ما را از این مقدار مشخص کرد. این خصوصیات همان چیزی است که هشیارها را بسیار مفید می کند.

چگونه از کلید خصوصی فرستنده برای امضای دیجیتالی مقدار هش استفاده می شود

فرستنده ما پیام خود را تایپ کرده است ، سپس آن را از طریق یک عملکرد هش قرار داده است ، که ما وانمود می کنیم مقدار آن را برگردانده است 10. پس از ارسال پیام هشدار دهنده ، می توانید با استفاده از کلید خصوصی خود در مقدار هش با فرمول زیر ، امضای دیجیتالی ایجاد کنید:

م (ج) = جد مود ن

این در واقع فرمولی برای رمزگشایی داده هایی است که با کلید عمومی گیرنده رمزگذاری شده است ، اما از آن برای امضای دیجیتالی اسناد نیز استفاده می شود.

هنگام صحبت از امضاهای دیجیتال:

• ارزش م (ج) امضا خواهد بود.
• ارزش ج هش پیام است (10).
• ارزش د بخشی از کلید خصوصی فرستنده است ، که قبلاً آن را گرفتیم (29).
• مود تابع همان عملیات باقیمانده است که قبلاً آنرا پوشش داده بودیم.
• ارزش ن بخش دیگری از کلید خصوصی فرستنده است ، که در ابتدا محاسبه کردیم (221).

بنابراین ، بیایید همه اینها را در فرمول خود قرار دهیم:

م (ج) = 1029 mod 221

    م (ج) = 100،000،000،000،000،000،000،000،000 مود 221

بیایید این کار را از طریق حسابگر مدول زیر اجرا کنیم (ما توضیح دادیم که چگونه این عملیات تحت عنوان کار می کنند کشف کلید عمومی بخش). برای اینکه این درست کار کند ، باید ورودی های خود را به این ترتیب تنظیم کنیم:

• عدد آ نوع – اعشاری
• عدد آ ارزش – 100000000000000000000000000000
• عدد ب نوع – اعشاری
• عدد ب ارزش – 221
• معادله محاسبه (این فقط کدی است که به ماشین حساب می گوید کدام عملیات را انجام می دهد. این و سایر کدها را می توانید در صفحه وب در بالای قسمت ورودی پیدا کنید) – وزارت دفاع (a، b)

اگر کارها را به درستی انجام داده اید ، باید مانند این باشد:

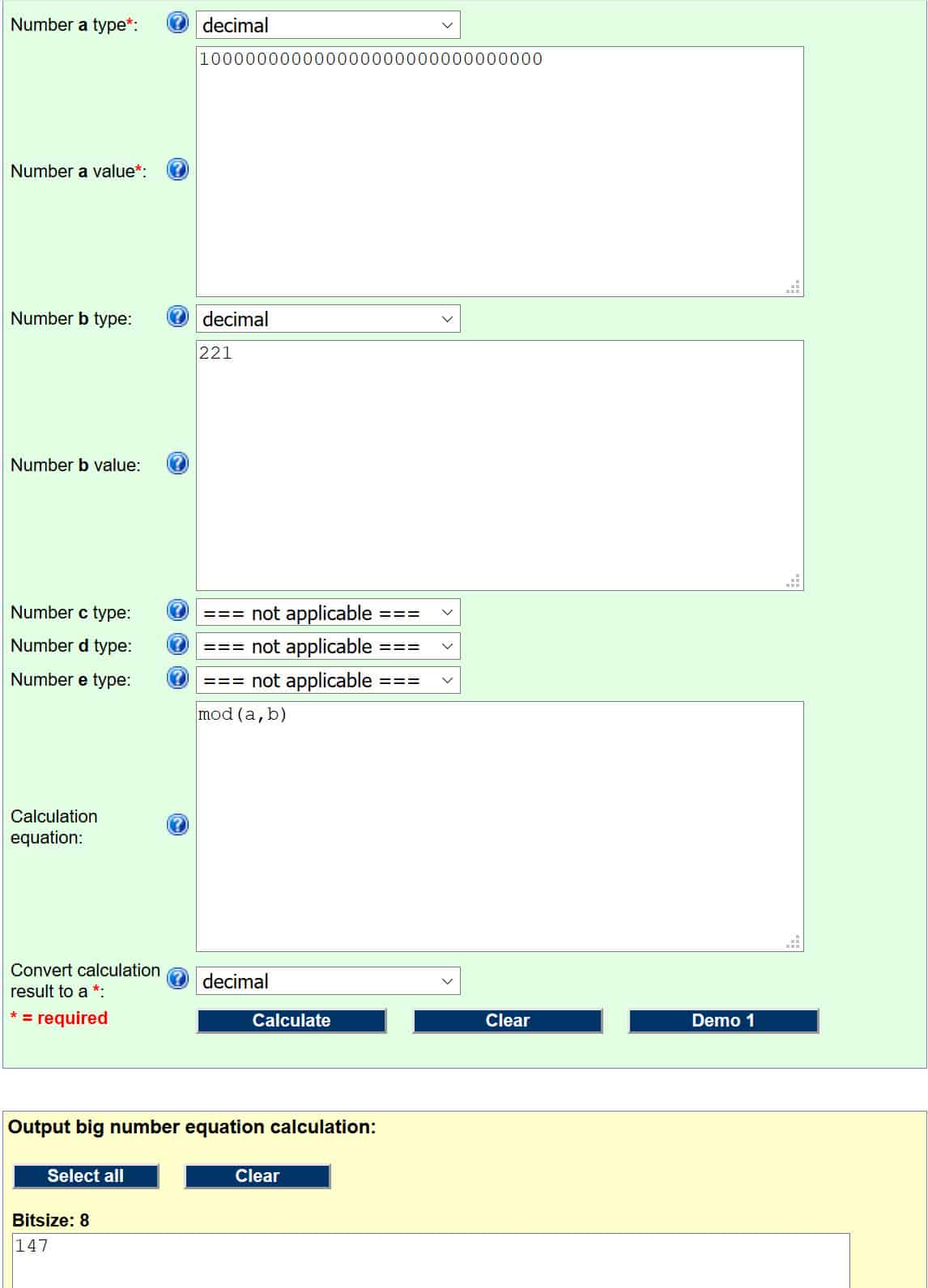
شماره موجود در جعبه زرد جواب ماست ، بنابراین امضای دیجیتالی برای هش پیام است 147.

برای اثبات صحت و صحت پیام ، همراه با ارائه عدم رد ، ارسال کننده ما پیام را ارسال می کند “امروز گرم است“در کنار امضای دیجیتال 147 به گیرنده مورد نظر خود فقط به یاد داشته باشید که ما به جای هش واقعی پیام ، از مقدار کمی برای هش برای ساده کردن موارد استفاده کردیم.

تأیید امضاهای دیجیتال

امضاهای دیجیتالی فقط درصورتی مفید هستند که بتوانیم صحت اثبات بودن آنها را بررسی کنیم. تا زمانی که کلید خصوصی فرستنده به خطر نیفتد ، گیرنده می تواند آزمایش کند که آیا یک پیام معتبر است یا خیر و با حفظ فرمول زیر در امضای دیجیتال ، صداقت خود را حفظ می کند:

    سانتی متر) = مه مود ن

در واژگونی روند امضای ، این در واقع فرمولی است که برای رمزگذاری داده ها در RSA استفاده می شود. وقتی از این فرمول برای تأیید امضاها استفاده می کنیم:

• ارزش سانتی متر) ارزش هش ارسال کننده در زمان امضای آن خواهد بود (با توجه به ساختار الگوریتم کلید عمومی RSA ، استفاده از کلید عمومی فرستنده از طریق این فرمول ، عملیات امضای را که ما تازه انجام دادیم خنثی می کند ، و ما را با داشتن هش اصلی وانمود کردن ما ترک می کند. ).
• ارزش م امضای دیجیتال است (147).
• ارزش ه بخشی از کلید عمومی فرستنده است ، که قبلاً آن را استخراج کردیم (5).
• مود تابع همان عملیات باقیمانده است که قبلاً آنرا پوشش داده بودیم.
• ارزش ن قسمت دیگر کلید عمومی فرستنده است ، که در ابتدا محاسبه کردیم (221).

بیایید همه آنرا به فرمول بیاندازیم:

    سانتی متر) = 1475 mod 221

    سانتی متر) = 68،641،485،507 مود 221

بیایید از همان ماشین حساب مدول مانند گذشته استفاده کنیم و همه چیز را یکسان نگه داریم ، به جز:

• عدد آ ارزش – 68،641،485،507

اگر موارد را به درستی وارد کرده اید ، باید نتیجه ای بدست آورید:

سانتی متر) = 10

اکنون که گیرنده مقدار هش را از امضای دیجیتال محاسبه کرده است ، مرحله بعدی محاسبه مقدار هش پیامی است که دریافت کرده اند ، “امروز گرم است” اگر از گذشته به خاطر دارید ، ما واقعاً از پیام واقعی SHA-256 استفاده نکردیم ، زیرا این تعداد خیلی بزرگ بود و نمونه را بسیار پیچیده می کردیم.

در عوض ، ما وانمود کرده ایم که عملکرد هش در واقع تعداد کمی را به ما داده است, 10, برای ورودی ما از آنجا که توابع هش همیشه همان نتیجه را برای ورودی معین تولید می کنند ، وقتی گیرنده ما “امروز گرم استاز طریق عملکرد هش خیالی ما ، آنها نیز ارزش این را دریافت می کردند 10.

فرآیند تأیید امضا به دو مقدار منجر می شود. مقدار اول هشی است همانطور که وقتی فرستنده به صورت دیجیتالی آن را با کلید خصوصی خود امضا کرد. ما این مورد را با استفاده از کلید عمومی فرستنده محاسبه کردیم.

مقدار دوم هش پیامی است که گیرنده دریافت کرده است. این با استفاده از همان عملکرد هش محاسبه می شود که فرستنده از آن برای پیام اصلی خود استفاده می کند. این دو مقدار سپس مقایسه می شوند و اگر مقادیر یکسان باشند ، پس می توانیم فرض کنیم که پیام معتبر است ، یکپارچگی آن را حفظ می کند ، و غیر قابل انکار است. البته این فرض می کند که کلید خصوصی فرستنده به خطر نیفتاده است.

از آنجا که نمونه ما یک مقدار از بازگشت 10 برای هش هنگام امضای ارسال کننده و همچنین مقدار آن 10 به عنوان هش پیامی که دریافت شد ، می توانیم فرض کنیم که این پیام ، “امروز داغ است “ از شخصی که ادعا می کند آنرا ارسال کرده است ، می آید و از زمان ارسال نیز تغییر نکرده است.

اگر گیرنده بخواهد پاسخ دهد تا خبرنگار آنها بتواند پیام خود را به همان شیوه تأیید کند ، کل روند تکرار می شود ، به جز کلیدهای خصوصی و عمومی گیرنده برای پروسه های امضاء و تأیید به ترتیب استفاده می شوند.

همه این ریاضیات ممکن است تمام ایده های امضاهای دیجیتالی را از شما دور کند. نگران نباشید ، زیرا پیاده سازی های RSA این فرآیند را به صورت خودکار انجام می دهد ، بنابراین مجبور نیستید شماره های خود را جمع کنید.

جوانب مثبت RSA & منفی

RSA یکی از الگوریتم های امضای دیجیتالی است که به طور گسترده پشتیبانی و اجرا می شود ، اگرچه حرکت به سمت الگوریتم های جدیدتر ، کارآمدتر و مطمئن تر مانند ECDSA و EdDSA وجود دارد..

در مقایسه با DSA (که در بخش بعدی به آن خواهیم پرداخت) ، RSA در تأیید امضا سریعتر است ، اما در تولید آنها کندتر است. از آنجا که امضاها یک بار ایجاد می شوند و بارها تأیید می شوند ، معمولاً RSA بر DSA ارجحیت دارد.

DSA

امنیت الگوریتم امضای دیجیتال بر اساس دو مفهوم ریاضی ، مسئله لگاریتم گسسته و برخی از خصوصیات افشای مدولار است. برای بعضی از گروهها محاسبه لگاریتم های گسسته آنها با تکنیک ها و فناوری های فعلی غیرممکن است.

تولید کلید DSA

برای تولید کلیدهای DSA ، اولین قدم انتخاب پارامترهایی است که گروهی از کاربران در همان سیستم می توانند از آنها برای تولید یک جفت کلید استفاده کنند..

تولید پارامترها

• انتخاب یک عملکرد هش – SHA-256 رایج ترین گزینه برای برآورده کردن الزامات امنیتی مدرن است.
• تنظیم طول کلید, ل و ن – این روزها, ل باید حداقل 2،048 بیت طول داشته باشد ، در حالی که ن باید حداقل 256 بیت باشد.
• تصمیم گیری در مورد نخست وزیر, ق, طول آن به همان طول است ن.
• نخست را انتخاب کنید, پ, جایی که پ-1 چند برابر است ق.
• یک شماره را انتخاب کنید, گرم, با استفاده از فرمول زیر (جایی که ساعت یک عدد دلخواه بین 1 و p-1):

گرم = ساعت(پ – 1) /ق مود پ

به طور معمول ، این مقادیر برای اطمینان از الگوریتم تعداد بسیار زیادی هستند. برای جلوگیری از محاسبه یا توضیح مثال بسیار دشوار ، از اعداد بسیار کمتری استفاده می کنیم که در واقع امن نیستند. بیایید بگوییم که:

    ق = 5

    پ = 11

برای پیدا کردن گرم, ما شماره های خود را به فرمول وصل می کنیم. ما استفاده خواهیم کرد 3 به عنوان ارزش ما برای ساعت:

گرم = 3 (11-1) / 5 mod 11

گرم = 32 مود 11

گرم = 9 مود 11

ما از همان ماشین حساب مدول مانند در استفاده خواهیم کرد چگونه از کلید خصوصی فرستنده برای امضای دیجیتالی مقدار هش استفاده می شود بخش. پارامترها یکسان خواهند بود ، به جز:

• عدد آ ارزش – 9
• عدد ب ارزش – 11

اگر همه چیز را به درستی وارد کرده باشید ، نتیجه ای را برای شما رقم خواهد زد گرم از 9.

ایجاد کلیدهای کاربر

کاربران انفرادی سپس این پارامترها را می گیرند و از آنها برای تشکیل جفت اصلی خود استفاده می کنند:

• کلید خصوصی (ایکس) یک عدد در بین است 0 و ق, که ما در 5 قرار داده ایم. برای مثال ما انتخاب خواهیم کرد 2 تا باشد ایکس, کلید خصوصی ما.
• کلید عمومی (ی) با استفاده از فرمول زیر محاسبه می شود:

    ی = گرمایکس مود پ

از این رو:

ی = 92 مود 11

ی = 81 مود 11

ما یکبار دیگر از همان ماشین حساب مدول استفاده خواهیم کرد. پارامترها یکسان خواهند بود ، به جز:

• عدد آ ارزش – 81
• عدد ب ارزش – 11

اگر موارد را به درستی وارد کرده اید ، باید نتیجه آن را بدست آورید y = 4. بنابراین کلید عمومی است 4.

اکنون که ما تمام ارزشهای خود را ایجاد کردیم ، اجازه می دهیم سریعاً به شما گزارش دهیم. پارامترهای سیستم عبارتند از:

• پ = 11
• ق = 5
• گرم = 9

جفت اصلی ما از این موارد تشکیل شده است:

• کلید خصوصی, ایکس = 2
• کلید عمومی, ی = 4

امضای دیجیتالی داده ها با DSA

فرستنده ها می توانند از کلید خصوصی DSA برای امضای دیجیتالی داده ها استفاده کنند ، این امر به گیرنده خود اجازه می دهد که صحت پیام را تأیید کند و صداقت آن را حفظ کند. همچنین مانع از رد شدن پیام برای ارسال کننده می شود.

فرآیند امضا با تولید یک مقدار تصادفی شروع می شود ک, که بین 1 و ق. برای این مثال ، بیایید فقط انتخاب کنیم 3 به عنوان شماره “تصادفی” ما, ک.

سپس فرمول زیر را برای ایجاد یک کلید شخصی دنبال می کنیم (r) برای پیام:

r = (گرمک مود پ) mod q

بیایید شماره های ما را بیاندازیم:

r = (93 مود 11) مود 5

r = (729 ماد 11) مود 5

ما دوباره وارد حساب ماشین حساب خود می شویم 729 و 11, که به ما نتیجه می دهد 3. از این رو:

r = 3 مود 5

و بعد دوباره عمل ماژول را با مقادیر جدید تکرار می کنیم تا به ما بدهند:

r = 3

ارزش ما برای r به عنوان کلید پیام استفاده می شود.

ما با بخش دیگری از امضای دیجیتال آشنا می شویم, s, با فرمول زیر:

s = ک-1(ح(م) + xr) مود ق

ک-1 نشان دهنده قدرت منفی نیست ک, اما در عوض همان معکوس ماژولار معکوس را محاسبه می کنیم فهم زیر بخش کلید خصوصی در قسمت قبلی مقاله که در مورد RSA صحبت کردیم.

ح(م) مقدار هش برای پیام ارسال شده توسط فرستنده است. به طور معمول ، این یک مقدار هش طولانی است که از پیام دریافت می شود ، دقیقاً مانند درک مقادیر هش بخش فوق ، که ما وقتی در مورد الگوریتم RSA صحبت می کردیم را پوشش دادیم.

برای این مثال ، ما امور را ساده نگه خواهیم داشت. درست مانند بخش RSA ، ما پیام خود را خواهیم گفت, م, است “امروز گرم است“ و این هش پیام است ح(م) ، 10 است.

بنابراین بیایید تمام ارزشهای ما را وارد فرمول کنیم:

s = 3-1 (10 + 2 x 3) (مود 5)

s = 3-1 (10 + 6) (مود 5)

s = 3-1 (16) (مود 5)

حال ، معکوس مدولار را از آن می گیریم 3 برای سفارش 5 (زیرا 5 ارزش ما برای ق) ، با استفاده از همان ماشین حساب معکوس مدولار از قبل. وارد 3 به عنوان عدد صحیح و 5 به عنوان مدول ، که به شما نتیجه می دهد 2. از این رو:

s = 2 (16) (مود 5)

s = 32 (مود 5)

بیایید برای عملکرد معمولی ماژولو به ماشین حساب ما برگردیم ، همان پارامترهایی را که قبلاً استفاده می کردیم حفظ کنیم ، به جز:

• عدد آ ارزش – 32
• عدد ب ارزش – 5

اگر این کار را به درستی انجام داده باشید ، ارزش آن را می دهد s از 2. امضای دیجیتالی از آن تشکیل شده است r و s (به ترتیب 3 و 2). فرستنده ها امضای دیجیتالی را در کنار پیام خود به گیرنده خود انتقال می دهند ، “امروز گرم است” آنها همچنین مقادیر اشتراک را به اشتراک می گذارند p ، q, گرم و ی با گیرنده آنها.

تأیید امضاهای دیجیتال

وقتی گیرنده امضای دیجیتالی را در کنار پیام دریافت کند ، می تواند صحت و صحت پیام را با مجموعه محاسبات زیر تأیید کند.

اولین قدم ، یافتن هش پیامی است که دریافت کرده اند. گیرنده این کار را با اجرای کل پیام از طریق یک عملکرد hash انجام می دهد. برای ساده تر و مداوم کارها ، بیایید بگوییم که پیام پیام, ح(م) 10 است.

مقادیر زیر نیز به گیرنده ارسال شده است که آنها در فرآیند تأیید از آنها استفاده می کنند:

• امضای دیجیتالی (r، s) – 3، 2
• پ – 1
• q – 5
• g – 9
• y – 4

اولین محاسبه یافتن است W:

W = s-1 مود ق

دوباره ، s-1 نشانگر گرفتن معکوس مدولار است. بگذارید مقادیر خود را وارد کنیم:

W = 2-1 mod 5

ما از ماشین حساب معکوس مدولار از قبل استفاده خواهیم کرد. وارد 2 به عنوان عدد صحیح و 5 به عنوان مدول ، که به شما نتیجه می دهد 3 برای W. مرحله بعدی پیدا کردن است تو1 با فرمول زیر:

تو1 = ح(م) ایکس W مود ق

بگذارید مقادیر خود را بیاندازیم:

تو1 = 10 x 3 mod 5

تو1 = 30 مود 5

به حسابگر ماژول معمولی برگردید و همان پارامترهایی را که قبلاً استفاده می کردیم حفظ کنید ، به جز:

• عدد آ ارزش – 30
• عدد ب ارزش – 5

این نتیجه ای را به ما می دهد 0 برای تو1.

ما از فرمول بعدی برای ارائه استفاده می کنیم تو2:

تو2 = r ایکس W مود ق

بیایید شماره های خود را وارد کنیم:

تو2 = 3 x 3 mod 5

تو2 = 9 مود 5

سپس با استفاده از همان پارامترهای قبلی به سراغ ماشین حساب ماژول معمولی میرویم ، به جز:

• عدد آ ارزش – 9
• عدد ب ارزش – 5

اگر به درستی وارد شوید ، نتیجه ای را برای شما به همراه خواهد داشت تو2 از 4.

اکنون که ارزشهای خود را برای آن داریم تو1 و تو2, ما میتوانیم پیدا کنیم v, با فرمول زیر:

v = (گرمu1یu2 مود پ) مود ق

بیایید شماره های ما را بیاندازیم:

v = (90 44 44 مود 11) مود 5

v = (1 x 256 mod 11) mod 5

v = (256 مود 11) مود 5

ما با استفاده از همان پارامترهای قبلی به حسابگر ماژولار معمولی خود برمی گردیم ، به جز:

• عدد آ ارزش – 256
• عدد ب ارزش – 11

این نتیجه ای را به ما می دهد 3. از این رو:

v = 3 مود 5

سپس ما یک بار نهایی ، دوباره با همان پارامترها از ماشین حساب ماژولال معمولی استفاده می کنیم ، به جز:

• عدد آ ارزش – 256
• عدد ب ارزش – 11

این به ما نتیجه می دهد v از 3.

اگر پیام معتبر است و با آن دستکاری نشده است ، پس v برابر با r خواهد بود:

    v = 3

    r = 3

    3 = 3

بنابراین این پیام توسط صاحب کلید خصوصی ارسال شده است و از زمان امضای آن پیام تغییر نکرده است.

جوانب مثبت DSA & منفی

امنیت DSA به استفاده از اعداد کافی وابسته است. بعلاوه p ، q و گرم رعایت پارامترهای صحیح ، مقدار ک همچنین باید تصادفی باشد. این نباید یک مقدار قابل پیش بینی باشد ، یا یک مقدار است که چندین بار استفاده می شود. در صورت عدم رعایت این الزامات ، کلید می تواند توسط یک مهاجم بازیابی شود.

با وجود این امکان, DSA تا زمانی که به درستی اجرا شود از مقادیر کافی استفاده می کند ، به طور کلی ایمن تلقی می شود. اگرچه نسبتاً ایمن است ، DSA در مقایسه با RSA یا سایر روشهای امضای دیجیتال تمایل به اجرای چندانی ندارد. با RSA مقایسه می شود ، می تواند کلیدها را سریعتر تولید کند و همچنین در تولید امضاهای دیجیتال سریعتر عمل می کند اما در تأیید آنها کندتر است.

نسخه 7.0 OpenSSH به طور پیش فرض پشتیبانی از کلیدهای DSA را متوقف کرده است ، که به نظر می رسد نشانه این است که دنیا در حال گذر از DSA و دیگر الگوریتم های دیگر است.

ECDSA & EdDSA

RSA و DSA تنها الگوریتم های امضای دیجیتال نیستند ، و همچنین مناسب ترین برای همه شرایط نیستند. طیف دیگری از افراد نیز وجود دارد ، مانند ECDSA و EdDSA, که دارای خواصی هستند که آنها را در شرایط خاص ترجیح می دهند.

متأسفانه ، اینها به ریاضیات پیچیده تری ، مانند منحنی بیضوی و رمزنگاری منحنی ادواردز متکی هستند. ما امروز به دلیل همین پیچیدگی اضافه نمی خواهیم آنها را با جزئیات بیشتری پوشش دهیم ، اما در مورد برخی از موارد مثبت و منفی آنها صحبت خواهیم کرد.

ECDSA

الگوریتم امضای دیجیتال منحنی Elliptic منحنی تنوع DSA است که شامل رمزنگاری منحنی بیضوی است. سطح امنیتی مشابهی را برای RSA فراهم می کند ، اما با یک کلید بسیار کوچکتر. این باعث می شود در اکثر جنبه های عملکرد ، از RSA یا DSA کارآمدتر باشد.

EdDSA

این یکی دیگر از گزینه های DSA است ، به استثنای آن که بر اساس منحنی های Twisted Edvard است. به نسبت الگوریتمها تقریباً جدید هستند که هم مزایا و هم مضرات آن را دارد. از طرف مثبت ، از تکنیک های جدیدتری استفاده می کند که به عملکرد آن می افزاید.

متأسفانه ، الگوریتم های جدیدتر در معرض دقت قرار نگرفته اند ، بنابراین بسیاری از افراد هنگام تصمیم گیری در مورد اجرای یا عدم اجرای آنها ، محتاط هستند..

با وجود این ، استفاده از EdDSA سطح بالایی از عملکرد را فراهم می کند, مقاومت در برابر حملات کانال جانبی ، و نیاز به یک شماره تصادفی منحصر به فرد در هر امضا را از بین می برد. در این مرحله ، EdDSA امیدوارکننده به نظر می رسد و شروع به دیدن اجرای گسترده تر خواهد کرد ، اما ما باید صبر کنیم و ببینیم که آیا مطالعات آینده حفره های امنیتی را پیدا می کند یا خیر..

گواهی های دیجیتال

هر کسی می تواند به راحتی یک جفت کلیدی ، حتی یک مهاجم بسازد. بنابراین آنچه که کسی مانع از ایجاد کلیدهای مختلف و تظاهرات رئیس جمهور می شود یا مانند هر کس دیگری نیست?

خوب ، هیچ چیز کسی را از ادعای شخص دیگری باز نمی دارد ، اما سیستمی وجود دارد که به دیگران اجازه می دهد تشخیص دهند که آیا شخص واقعاً همان کسی است که ادعا می کند یا خیر. آن را به نام زیرساخت کلید عمومی (PKI), و شامل می شود گواهی های دیجیتالی که کلید عمومی یک شخص یا شخص را به هویت واقعی آنها پیوند می دهد. این گواهینامه ها توسط دیگران امضا شده اند تا نشان دهند چقدر باید به گواهی اعتماد شود.

برای تأیید اسناد می توانید فرایند را با استفاده از اسناد رسمی مقایسه کنید. اگر کسی نسخه ای از شناسنامه داشته باشد ، ممکن است در مورد اینکه آیا این مشروعیت دارد یا خیر ، شکاک باشید. اگر همان شناسنامه توسط یک دفتر اسناد رسمی امضا شده و مهر شده باشد ، خیلی بیشتر احتمال دارد که باور داشته باشید که این یک نسخه واقعی است.

چرا?

از آنجا که امضا و تمبر نشان می دهد که یک نهاد عمومی معتبر فرد و شناسنامه اصلی آنها را دیده است ، پس تأیید کرد که نسخه در واقع قانونی است. دفتر اسناد رسمی کپی شناسنامه را تأیید می کند و شهرت خود را در پشت آن با امضای و مهر خود ثبت می کند.

امانتی که به دفتر اسناد رسمی داریم به نسخه کپی شناسنامه منتقل می شود و به ما این امکان را می دهد که به آن اعتماد کنیم به مراتب بیشتر از یک مورد که محضری نشده است..

دو نوع عمده صدور گواهینامه وجود دارد ، جمقامات برتر (CA) و شبکه اعتماد.

مقامات گواهی

مقامات گواهینامه هستند سازمانهای معتبری که افراد یا اشخاصی را بررسی می کنند تا تأیید کنند که آیا آنها صاحب قانونی یک کلید عمومی هستند یا خیر. اگر چک ها فاش کنند که فرد مالک واقعی است ، پس از آن مجوز گواهی را با کلید خود امضا می کند ، این نشان می دهد که این چک را به اتمام رسانده و معتقد است که کلید شخصی و عمومی به طور قانونی پیوند خورده است..

تا زمانی که به مرجع صدور گواهینامه و روند تأیید کلید آنها اعتماد داشته باشیم ، می توانیم به گواهی نامه امضا شده توسط آنها اعتماد کنیم, و به این ترتیب که کلید عمومی نمایانگر آن فرد است.

بسته به نوع گواهینامه و کاربرد آن ، سطوح مختلف می توانند فرایندهای تأیید متفاوتی داشته باشند و در نتیجه اعتماد به نفس بالاتری را نشان می دهند.

وب اعتماد

شبکه اعتماد تحت فرض مشابه عمل می کند ، به جز tدر اینجا هیچ بدن مرکزی وجود ندارد مانند مقامات گواهینامه که مراحل تأیید را انجام می دهند و گواهی نامه ها را امضا می کنند.

در عوض ، وب اعتماد به افراد دیگر متکی است تا بتوانند گواهی نامه ها را امضا کنند و اعتبار خود را در پیوند بین فرد و کلید عمومی قرار دهند. این سیستم بیشتر با PGP مورد استفاده قرار می گیرد که در آن کاربران می توانند به راحتی گواهینامه های خود را تهیه کنند.

اینگونه کار می کند:

بگذارید بگوییم شما دو دوست دارید که می خواهند گواهینامه هایشان امضا شود تا ثابت کنند که آنها صاحبان قانونی کلیدهای عمومی مربوطه هستند. شما این افراد را به خوبی می شناسید ، و آنها شناسنامه های دولتی خود را به شما نشان می دهند ، این باعث می شود که شما به طور کامل مطمئن شوید که آنها هستند که می گویند هستند و به این ترتیب صاحبان واقعی کلیدهای عمومی که ادعا می کنند هستند..

از آنجا که می دانید که آنها صاحبان مشروعیت کلیدهای عمومی خود هستند ، شما خوشحال هستید که از کلید خصوصی خود برای امضای گواهینامه های خود استفاده می کنید ، شهرت خود را بر روی آنها می گذارید و اساساً میگویید “بله ، من هویت این افراد را تأیید کردم و آنها چه کسانی هستند آنها ادعا می کنند “. این دو دوست بعد می توانند همین کار را برای شما انجام دهند.

بیایید بگوییم که هر دو دوست شما دارای دو دوست دیگر هستند که می خواهند گواهی های خود را امضا کنند. اگر دو دوست شما این گواهینامه های دیگر را امضا می کنند ، می توانید از اعتمادی که به دوستانتان دارید استفاده کنید تا بپذیرید که این افراد دیگر واقعاً همان کسانی هستند که می گویند آنها نیز هستند.

دوستان دوستان شما می توانند گواهینامه های افرادی را که به آنها اعتماد دارند و امثالهم از این طریق امضا کنند ، سرانجام شبکه بزرگی از افراد مورد اعتماد را بسازند. هنگامی که این شبکه ها به اندازه کافی بزرگ شوند و با دیگر شبکه ها بهم متصل شوند, آنها می توانند به عنوان ابزاری برای اعتماد به هر کس دیگری در شبکه استفاده شوند.

امضای بیشتر در مورد گواهینامه ، به ویژه اگر امضایی از افراد بسیار معتبر باشد, بیشتر می توانید به گواهی دیجیتال شخصی و پیوند بین کلید عمومی و هویت آنها اعتماد کنید.

کاربران PGP غالباً مهمانی هایی را امضا می کنند که افراد در آنجا گرد هم می آیند تا هویت خود را بررسی و گواهی های دیجیتالی خود را امضا کنند. این اجتماعات به ورود افراد جدید به شبکه کمک می کند.

اگرچه با برخی از پیچیدگی ها همراه است ، اما مزیت وب سایت سیستم اعتماد این است که هیچ بدنه مرکزی قابل تخریب نیست.

آیا امضاهای دیجیتال ایمن هستند?

به معنای کلی, امضاهای دیجیتال ایمن هستند مگر اینکه کلید خصوصی فرد ثبت شده به خطر بیفتد. اگر مالک به شخص دیگری اطلاع داده است ، کلید خصوصی را رها کرده یا آن را به طریقی دیگر دزدیده اید ، پس برای مهاجمین امکان دارد پیام ها را به صورت دیجیتالی امضا کند که گویی آنها مالک آن هستند..

این می تواند به مهاجمی منجر شود که از قربانی خود جعل کند یا اطلاعات خود را دستکاری کند. این یک مسئله امنیتی بزرگ است و هرکسی که گمان می کند کلید آنها به خطر بیافتد ، باید گواهی دیجیتالی خود را که آنها را به کلید عمومی خود پیوند می دهند ، ابطال کند ، و یک شماره جدید صادر کند.

درمورد امنیت امضاهای دیجیتالی چند هشدار دیگر وجود دارد. باید از الگوریتم امضای دیجیتالی مناسب استفاده شود ، همچنین باید به درستی اجرا شود. در کنار این ، معمولاً باید از طریق گواهی دیجیتال راهی برای پیوند دادن کلید عمومی به صاحب آن نیز وجود داشته باشد.

تا زمانی که این الزامات برآورده شود ، شما بهترین شیوه های صنعت را دنبال می کنید ، و کلید خصوصی شما به خطر نمی افتد امضاهای دیجیتال روشی عالی برای تهیه اصالت ، صداقت و عدم رد اطلاعات به داده ها است.

داده های ساختاری توسط کای Stachowiak تحت مجوز CC0