Ce sunt semnăturile digitale și cum funcționează?

Semnăturile digitale sunt ca versiunile electronice ale semnăturilor tale scrise de mână. Ele permit oamenilor să verifice autenticitatea și integritatea datelor, precum și împiedicarea semnatarului de a-și putea respinge (nega) implicarea.

Aceste proprietăți au dus la adoptarea de semnături digitale într-o gamă largă de aplicații, incluzând multe dintre protocoalele noastre de securitate, e-mail securizat și în gestionarea drepturilor digitale..

În acest articol, vom discuta ce sunt semnăturile digitale, unde sunt utilizate, precum și detaliile tehnice ale doi dintre cei mai populari algoritmi, RSA și DSA.

Ce sunt semnăturile digitale?

După cum am spus mai sus, semnăturile digitale ne oferă trei proprietăți foarte importante. Acestea sunt autentificarea, integritatea și non-repudierea.

Autentificare este procesul de verificare a faptului că individul care trimite un mesaj este cu adevărat cine spune că sunt și nu un impostor.

integritate de date sau de un mesaj se referă la faptul că au ajuns în aceeași stare ca și când au fost trimise. Dacă un mesaj a fost modificat sau modificat, acesta nu-și mai păstrează integritatea.

Dacă date sau un mesaj este non-repudiable, înseamnă că autorul său nu poate contesta faptul că au fost adevăratul creator al documentului. Această proprietate îndepărtează credibilitatea plauzibilă sau vechea scuză „Îmi pare rău, prietenul meu folosea contul”.

Atâta timp cât cheia privată a persoanei nu a fost compromisă, semnăturile digitale pot furniza date tuturor celor trei proprietăți.

Este posibil să vă întrebați de ce avem nevoie de aceste proprietăți în primul rând. Să facem un pas înapoi și să ne gândim la cum facem lucrurile într-o întâlnire față în față.

Să spunem că îți datorezi prietenului tău Mike $ 100. Ești o persoană bună, așa că ești fericit să-i plătești înapoi atunci când vei primi banii.

Cel mai bun mod de a face acest lucru ar fi să îi dai doar o factură de 100 USD lui Mike. Îl cunoști de ani buni și știi cum arată, așa ar fi ușor să-i verifici identitatea și astfel să autentifici că dai banii persoanei potrivite.

Dacă ai fi cu adevărat anal, ai putea chiar să-l verifici și să-l faci să semneze o primire scrisă de mână pentru tine. Semnătura de pe chitanță i-ar conferi integritate și ar face-o ireproșabilă.

Dar dacă în loc să efectuați tranzacția față în față, ați primit un apel de la cineva care să spună că sunt Mike și că ar trebui să trimiteți 100 USD la numărul de cont 12345678.

„Dar nu sună ca Mike”, spui.

“Am o răceală. Trimite-o acum, am nevoie de bani. ”

Ai trimite banii? Probabil ca nu.

Nu există nicio modalitate de a ști dacă este cu adevărat Mike sau numărul corect al contului. Pentru tot ce știi, ar putea fi un impostor care încearcă să fure de la tine. În loc să transferați banii imediat, cel mai bine ar fi să așteptați până îl veți vedea pe Mike, astfel încât să îi puteți da banii în persoană.

La fel ca în scenariul de mai sus, întâlnim frecvent situații în care trebuie verificați identitatea unei părți sau integritatea datelor din lumea online. Acesta este motivul pentru care semnăturile digitale au crescut ca un mecanism care poate oferi aceste proprietăți și poate facilita tranzacțiile online sigure.

Fără ei, s-ar putea să nu știm cu cine vorbim, nu am putea fi siguri dacă datele au fost sau nu manipulate, iar persoana ar putea nega că au fost responsabili.

Utilizările semnăturilor digitale

Aceste proprietăți ale semnăturilor digitale le fac utile într-o mare varietate de aplicații. Acestea sunt adesea utilizate singure sau în combinație cu criptarea într-o serie de protocoale de securitate diferite, cum ar fi:

• IPsec
• SSH
• TLS

De asemenea, sunt frecvent utilizate în gestionarea drepturilor digitale, în tehnologia blockchain, în gestionarea contractelor aplicații, ca parte a distribuție software, si in finanţa.

Istoricul semnăturilor digitale

Ideea semnăturilor digitale a fost prima dată plutită de criptografii renumiți Whitfield Diffie și Martin Hellman în lucrarea lor din 1976 Noi direcții în criptografie. În 1978, Ronald Rivest, Adi Shamir și Len Adleman au adus în viziunea publicului algoritmul RSA, care ar putea fi folosit pentru a produce semnături digitale nesigure..

A fost nevoie de încă un deceniu pentru ca semnăturile digitale să apară într-o aplicație larg răspândită: lansarea Lotus Notes 1.0 a IBM. De atunci, semnăturile digitale au început să vadă adoptarea mai largă pe măsură ce apar tehnici noi și nevoia de autentificare online și verificări de integritate a crescut.

O scurtă introducere în criptografia cu chei publice

Înainte de a intra în semnături digitale, cel mai bine este să acoperim unele dintre aspectele importante ale criptografiei cu chei publice, care stau la baza modului de funcționare a semnăturilor digitale.

Dacă sunteți relativ nou la criptografie, sistemul cu care veți fi cel mai familiar este criptarea cu cheie simetrică. Acest lucru înseamnă doar că aceeași cheie (care este similară cu o parolă, dar are unele diferențe) este folosită atât pentru criptarea, cât și pentru decriptarea datelor.

Criptarea cu chei publice a fost o revoluție, deoarece a implicat folosind chei separate pentru procesul de criptare și decriptare, ceea ce duce la o serie de aplicații criptografice diferite. Aceste două chei au format o pereche de chei, formată din cheia publică și cea privată. Cheia publică poate fi, în mod evident, partajată public, în timp ce cheia privată trebuie păstrată secretă pentru ca sistemul să fie securizat.

Cele mai frecvente două utilizări ale criptografiei cu cheie publică sunt criptarea și semnăturile digitale.

Criptarea

Una dintre caracteristicile de bază ale criptografiei cu cheie publică a fost aceea permite părților care nu s-au întâlnit niciodată să își transmită mesaje confidențiale reciproc. Expeditorul caută cheia publică a destinatarului dorit (acestea pot fi găsite pe serverele de chei publice, pe site-urile personale sau pur și simplu solicitând individului), apoi criptează un mesaj cu această cheie, înainte de a o trimite destinatarului..

Destinatarul este singura persoană care poate accesa mesajul – presupunând că cheia privată nu a fost compromisă – decriptând-o cu cheia lor privată. Chiar dacă cheia publică a fost utilizată pentru criptarea mesajului, aceasta poate fi decriptată doar de cheia privată. Dacă destinatarul dorește să răspundă, găsește cheia publică a expeditorului inițial, apoi repetă procesul.

Vedeți și: Tipurile de criptare comune explicate

Cum funcționează semnăturile digitale?

Așa cum am spus, semnăturile digitale sunt utilizate pentru autentificare, pentru a vedea dacă datele au fost modificate și pentru a ne-repudia. Există o serie de mecanisme diferite care pot fi utilizate pentru semnăturile digitale și au fiecare variații ușoare în modul în care sunt structurate.

În general, acești algoritmi trebuie să fie compuse din trei sub-algoritmi:

• Un algoritm de generare cheie – Acest algoritm generează o pereche de chei aleatoare pentru un utilizator. Numerele implicate în perechea de chei trebuie să respecte anumite parametri pentru a fi considerați siguri. Două dintre cele mai importante aspecte sunt că numerele sunt suficient de aleatorii și de dimensiuni adecvate.
• Un algoritm pentru semnarea datelor – Odată ce un utilizator are cheile sale, există modalități specifice de aplicare a datelor la procesul de semnătură.
• Un algoritm pentru verificarea semnăturii – De asemenea, verificarea unei semnături urmează un proces prestabilit.

Pentru ca un sistem de semnătură digitală să fie eficient, acesta trebuie să fie structurat astfel încât:

• Datele semnate cu o cheie privată sunt verificată cu cheia publică potrivită de aceeași persoană.
• Ar trebui să fie în esență imposibil (folosind tehnologia și tehnicile actuale) să falsifice o semnătură valabilă fără să știi cheia privată a individului.

Unele dintre cele mai frecvente scheme de semnătură digitală includ RSA, DSA, EcDSA și EdDSA.

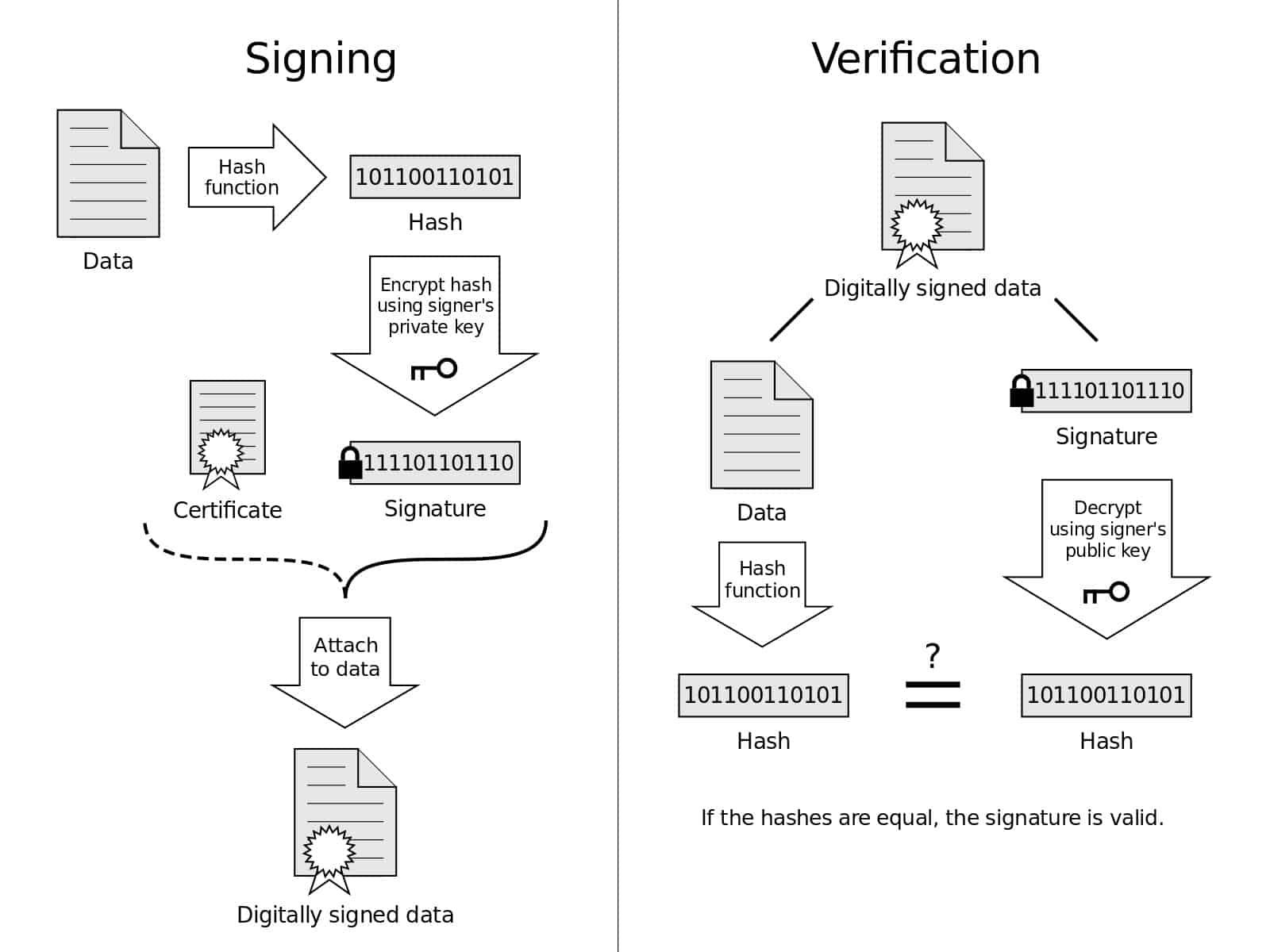
Această imagine oferă o reprezentare vizuală a proceselor de semnare și verificare. Diagrama semnăturii digitale de Acdx licențiat sub CC0

RSA

RSA a fost primul algoritm de semnătură digitală, dar poate fi folosit și pentru criptarea cu chei publice. În acest articol, vom sări peste aspectul de criptare, dar puteți afla mai multe despre el în articolul nostru cuprinzător care acoperă ce este RSA și cum funcționează..

Generare cheie RSA

În implementările sigure ale RSA, perechile de chei vor fi stabilite în mod automat în cadrul următorului proces:

Generație primă

Sunt selectate două numere prime individuale, p și q. Mărimea exactă a acestor prime va varia în funcție de dimensiunea cheii. În aceste zile, un minim de chei RSA de 2048 biți sunt, în general, recomandate pentru o securitate adecvată, deci vorbim despre două numere prime care se înmulțesc pentru a produce un număr de 2048 biți..

2048 de biți este o dimensiune în sistemul de numere binare. Dacă un număr de această dimensiune a fost convertit în sistemul nostru zecimal mai familiar, ar fi aproximativ acest timp:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Primele din RSA trebuie selectate aleatoriu și trebuie să aibă lungimi similare.

În exemplul nostru, vom folosi numere mult mai mici pentru a face lucrurile mai ușor de înțeles. Fiți conștienți că utilizarea tastelor de această dimensiune ar face semnăturile digitale banale spre fals. Acesta este motivul pentru care valorile atât de mari sunt utilizate în practică.

Să spunem că:

p = 13

q = 17

Primul pas ar fi calcularea modulului n folosind următoarea formulă:

n = pq

n = 13 x 17

n = 221

Valoarea a n este de asemenea lungimea cheii.

Funcția totală a lui Carmichael

Acum că avem valoarea pentru n, următorul pas este să folosiți funcția totientă a lui Carmichael:

λ(n) = LCM (p – 1, q – 1)

Există câteva lucruri pe care trebuie să le înțelegeți:

• λ(n) înseamnă totientul lui Carmichael pentru valoarea lui n
• LCM reprezintă cel mai mic multiplicator comun. Acesta este cel mai scăzut număr comun ca ambele p-1 și q-1 se poate împărți în

Să ne conectăm cifrele la ecuație:

λ(221) = LCM (13 – 1, 17 – 1)

λ(221) = LCM (12, 16)

Dacă vă pricepeți la matematica mentală, este posibil să vă fi dat seama de asta 48 este cel mai scăzut multiplicator comun al ambelor 12 și 16. Acest lucru se datorează faptului că 48 este cel mai mic număr în care se pot încadra ambele numere (12 x 4 = 48, 16 x 3 = 48). Prin urmare:

λ(221) = 48

Venind cu cheia publică

În RSA, cheia publică este constituită din valoare n (pe care am calculat-o deja 221) și e. Deoarece cheia publică este distribuită liber, valoarea pentru e nu trebuie să fie un secret. De fapt, de cele mai multe ori este stabilită la 65.537, deoarece numerele mai mari ar încetini procesul de criptare. În exemplul nostru, vom seta e la 5, doar pentru a face un număr mic și simplu cu care să lucrezi.

Prin urmare, cheia publică pentru acest exemplu este alcătuită din 221 și 5. Vom acoperi specificul modului în care se aplică cheia publică în secțiunile următoare.

Descoperind cheia privată

La fel cum cheia noastră publică este formată din două numere, la fel și cheia noastră privată. Cheile private sunt alcătuite din d și e. Știm deja valoarea pentru e (5), și putem utiliza următoarea formulă pentru a găsi d:

d = 1 /e mod λ(n)

Rețineți că mod simbolizează doar o operație de modulo, ceea ce ar însemna în mod normal că trebuie să găsești restul odată ce împărțiți partea stângă de dreapta. Ca exemplu:

17 mod 3 = 2

Acest lucru se datorează faptului că 3 se potrivește cu 17 în total de 5 ori, cu restul de 2.

Exemplul nostru este puțin diferit. „1 /e mod”Segmentul ecuației poate părea că vă spune să împărțiți 1 de e, dar de fapt nu este. Este confuz, dar acesta este un mod de a reprezenta invers modular. Ecuația ne spune de fapt să calculăm inversul modular al e și λ(n).

Inversul modular este obținut în mod normal folosind algoritmul euclidian extins, dar nu vom acoperi acest lucru în acest articol. În schimb, vom folosi doar un calculator online pentru a facilita lucrurile.

Acum că ne-am extras din asta, hai să introducem valorile noastre în formula:

d = 1/5 mod 48

A găsi d, tot ceea ce trebuie să facem este să ne introducem valoarea e (5) în calculatorul online unde se spune întreg, atunci valoarea noastră pentru λ(n), care este 48, unde spune modulo.

Acest lucru ne oferă un rezultat al 29 conform calculatorului online. Prin urmare, cheia noastră privată va fi alcătuită din:

e = 5

d = 29.

Acum că am generat ambele chei, următoarea întrebare este „Ce facem cu ele?” Ei bine, i-am putea folosi pentru a cripta și decripta mesajele prin criptografia cu cheie publică, dar acest articol este despre semnături digitale, deci ne vom concentra pe asta.

Semnarea digitală a datelor cu RSA

Să spunem că cineva vrea să-i trimită un mesaj prietenului său, dar dorește să se asigure că prietenul poate verifica autenticitatea și integritatea mesajului. Ei ar putea face acest lucru folosind o semnătură digitală RSA pentru a semna mesajul.

Primul pas este să rulați întregul mesaj printr-o funcție hash. Acestea sunt funcții unidirecționale care furnizează întotdeauna aceeași ieșire pentru o intrare dată. Funcțiile hash sigure sunt în esență imposibil de inversat, ceea ce înseamnă că ieșirea nu poate fi utilizată pentru a da seama de intrare. De asemenea, este imposibil ca două mesaje separate să aibă aceeași ieșire.

Puteți afla mai multe despre funcțiile hash în Ce este hashing? Secțiunea articolului nostru, Criptare, degajare, sărare – care este diferența?

Să spunem că vrem să semnăm digital mesajul „Azi e cald”, Astfel încât destinatarul nostru să știe dacă mesajul este autentic sau nu și dacă a fost modificat. Deci, am alerga „Azi e cald”Printr-o funcție hash.

Înțelegerea funcțiilor hash

În aceste zile, funcția de hash sigură cea mai frecvent utilizată este SHA-256. Când ne trimitem mesajul printr-un calculator SHA-256 online, acesta ne oferă un astfel de rezultat:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Acest lucru ridică câteva probleme pentru exemplul nostru. Primul este că nu este un număr zecimal precum cele cu care sunt obișnuiți majoritatea oamenilor. Este posibil să fi observat că există litere în acest număr și că acestea merg doar la f. Acest lucru ne oferă un indiciu că este de fapt un număr hexadecimal.

sistemul hexadecimal se bazează pe o bază de 16, mai degrabă decât pe o bază de 10, ca sistemul de numere pe care îl folosim în mod normal. Acest lucru înseamnă că, în loc să numărați în multipli de 10, acesta contează în multipli de 16, iar primele 6 litere ale alfabetului nostru sunt folosite pentru a alcătui aceste numere suplimentare. Un număr ca acesta poate fi transformat în sistemul nostru zecimal de zi cu zi, dar acesta nu intră în sfera de aplicare a acestui articol.

A doua problemă pe care o avem este că acesta este un număr foarte mare. Dacă ar fi convertit în zecimale, ar fi și mai mult. Întrucât vizăm simplitatea din acest ghid, efectuarea calculelor cu un număr atât de mare ar face lucrurile prea confuze pentru a obține conceptele de bază.

Cu ideea de a demonstra cum funcționează semnăturile digitale RSA într-o manieră ușor de înțeles, nu vom folosi o valoare de hash atât de mare în exemplul următor. În schimb, ne vom preface că valoarea hașei din „Azi e cald”Este pur și simplu 10.

De asemenea, va trebui să ne prefacem că, ca orice hash real, ori de câte ori vom introduce aportul de „Este fierbinte azi” prin funcția de hash, va întoarce întotdeauna valoarea 10. Pentru a fi în concordanță cu modul în care funcționează hash-urile în mod normal, va trebui să ne prefacem că este foarte puțin probabil ca orice altă intrare să dea aceeași valoare. În mod similar, trebuie să ne prefacem că nu este posibil să ne dăm seama de contribuția noastră inițială din această valoare. Aceste proprietăți sunt cele care fac ca hașea să fie extrem de utilă.

Modul de utilizare a cheii private a expeditorului pentru a semna digital valoarea hash

Expeditorul nostru a scos mesajul lor, apoi l-a trecut printr-o funcție de hash, despre care pretindem că a returnat o valoare a acesteia 10. Odată ce expeditorul are hash-ul mesajului, poate crea semnătura digitală prin aplicarea cheii private la valoarea hash cu următoarea formulă:

m (c) = cd mod n

Aceasta este de fapt formula de decriptare a datelor care au fost criptate cu cheia publică a destinatarului, dar este folosită și pentru semnarea digitală a documentelor.

Când vine vorba de semnături digitale:

• Valoarea a m (c) va fi semnătura.
• Valoarea a c este hash-ul mesajului (10).
• Valoarea a d face parte din cheia privată a expeditorului, pe care am derivat-o mai devreme (29).
• mod funcția este aceeași operațiune rămasă pe care am acoperit-o anterior.
• Valoarea a n este cealaltă parte a cheii private a expeditorului, pe care am calculat-o la început (221).

Așadar, haideți să punem totul în formula noastră:

m (c) = 1029 mod 221

    m (c) = 100.000.000.000.000.000.000.000.000.000 mod 221

Haideți să executăm acest lucru prin următorul calculator de modulo (am explicat cum funcționează aceste operațiuni în baza Descoperind cheia publică secțiune). Pentru ca acesta să funcționeze corect, trebuie să ne setăm intrările ca:

• Număr A tip – zecimal
• Număr A valoare – 100000000000000000000000000000
• Număr b tip – zecimal
• Număr b valoare – 221
• Ecuația de calcul (acesta este doar codul care spune calculatorului ce operație trebuie efectuată. Acesta și alte coduri pot fi găsite pe pagina web legată deasupra secțiunii de intrare) – mod (a, b)

Dacă ați făcut lucrurile cum trebuie, ar trebui să arate astfel:

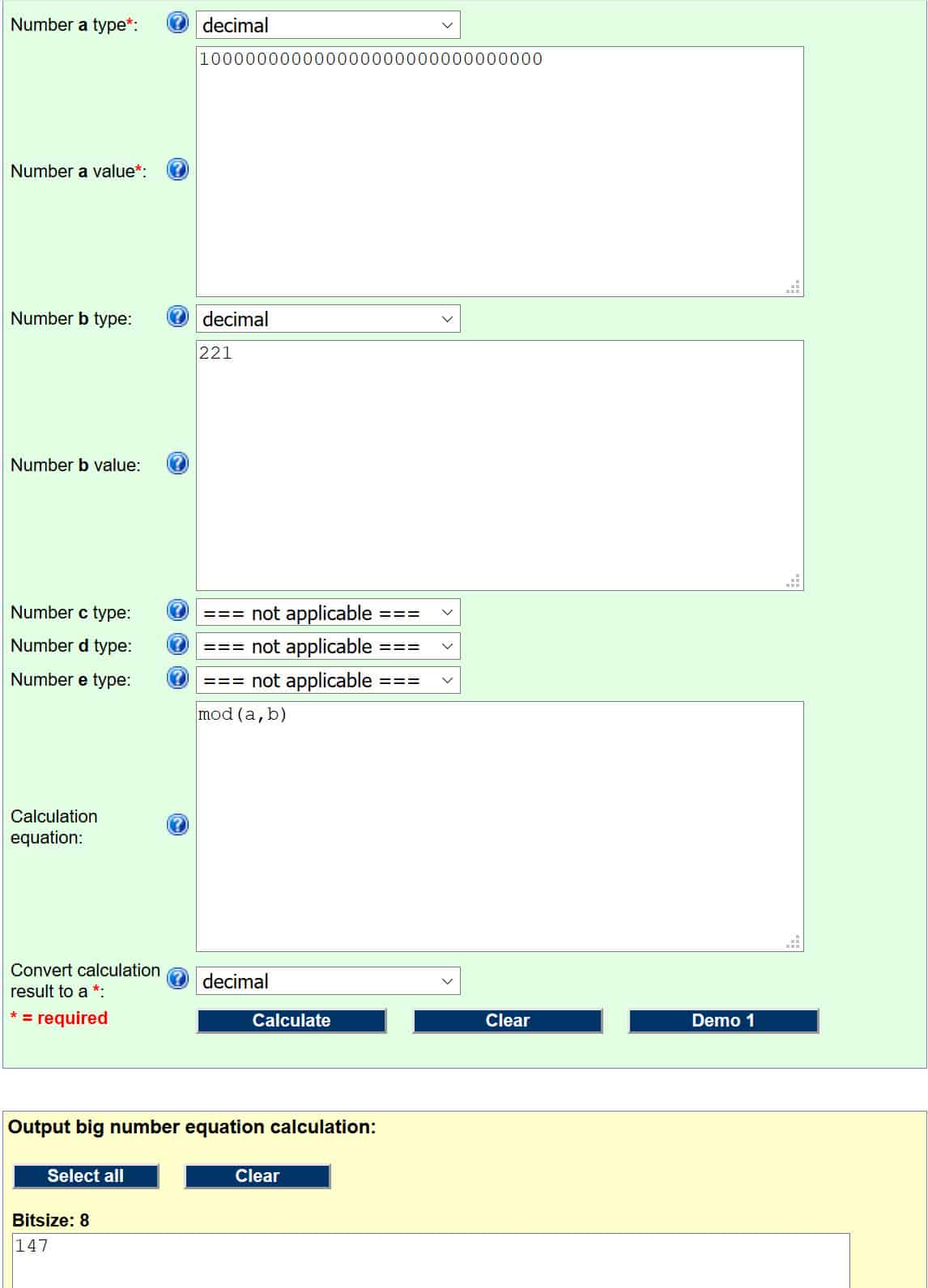
Numărul din căsuța galbenă este răspunsul nostru, deci semnătura digitală pentru hash-ul mesajului este 147.

Pentru a dovedi autenticitatea și integritatea mesajului, împreună cu furnizarea non-repudierii, expeditorul nostru va transmite mesajul „Azi e cald”Alături de semnătura digitală a 147 destinatarului dorit. Amintiți-vă doar că am folosit o valoare mică pentru hash pentru a simplifica lucrurile, în loc de hash-ul real al mesajului.

Verificarea semnăturilor digitale

Semnăturile digitale sunt utile numai dacă putem verifica dacă sunt legitime. Atâta timp cât cheia privată a expeditorului nu a fost compromisă, destinatarul poate testa dacă un mesaj este autentic și își păstrează integritatea aplicând următoarea formulă semnăturii digitale:

    cm) = me mod n

Într-o inversare a procesului de semnare, aceasta este de fapt formula care este utilizată pentru criptarea datelor în RSA. Când folosim această formulă pentru a verifica semnăturile:

• Valoarea a cm) va fi valoarea de hash a expeditorului la momentul semnării acesteia (datorită structurii algoritmului cheie publică RSA, aplicând cheia publică a expeditorului prin această formulă va anula operațiunea de semnare pe care tocmai am efectuat-o, lăsându-ne cu hash-ul nostru pretendent original) ).
• Valoarea a m este semnătura digitală (147).
• Valoarea a e face parte din cheia publică a expeditorului, pe care am derivat-o mai devreme (5).
• mod funcția este aceeași operațiune rămasă pe care am acoperit-o anterior.
• Valoarea a n este cealaltă parte a cheii publice a expeditorului, pe care am calculat-o la început (221).

Să aruncăm totul în formulă:

    cm) = 1475 mod 221

    cm) = 68.61.485.507 mod 221

Să folosim același calculator de modulo ca și înainte și să păstrăm totul la fel, cu excepția:

• Număr A valoare – 68641485507

Dacă ați introdus lucrurile corect, ar trebui să obțineți un rezultat din:

cm) = 10

Acum, după ce destinatarul a calculat valoarea hash din semnătura digitală, următorul pas este să calculeze valoarea hash a mesajului pe care l-a primit, „Azi e cald“. Dacă vă amintiți mai devreme, nu am folosit de fapt hash-ul SHA-256 adevărat al mesajului, deoarece numărul ar fi fost prea mare și a făcut exemplul prea complicat.

În schimb, ne-am prefăcut că funcția de hash ne-a dat de fapt numărul mic, 10, pentru aportul nostru. Deoarece funcțiile hash întotdeauna produc același rezultat pentru o intrare dată, atunci când destinatarul nostru pune „Azi e cald”Prin funcția noastră de hash imaginar, ei ar fi primit și valoarea de 10.

Procesul de verificare a semnăturii are ca rezultat două valori. Prima valoare este hash-ul așa cum a fost atunci când expeditorul a semnat-o digital cu cheia lor privată. Am calculat acest lucru mai sus folosind cheia publică a expeditorului.

A doua valoare este hash-ul mesajului pe care l-a primit destinatarul. Aceasta se calculează folosind aceeași funcție hash pe care expeditorul o folosea pentru a reda mesajul inițial. Aceste două valori sunt apoi comparate și dacă valorile sunt aceleași, atunci putem presupune că mesajul este autentic, își păstrează integritatea și că nu este respingibil. Desigur, acest lucru presupune că cheia privată a expeditorului nu a fost compromisă.

Deoarece exemplul nostru a returnat o valoare de 10 pentru hash când a fost semnat de expeditor, precum și o valoare de 10 ca hașa mesajului primit, putem presupune că mesajul „Este azi cald ” provine de la persoana care pretinde că a trimis-o și că nu a fost modificată de când a fost trimisă.

Dacă destinatarul dorește să răspundă, astfel încât corespondentul său să-și poată verifica mesajul în același mod, întregul proces este repetat, cu excepția cheilor private și a cheilor publice ale destinatarului sunt utilizate pentru procesele de semnare și verificare, respectiv.

Toate aceste matematică te-au putut scoate din ideea de semnături digitale. Nu vă faceți griji, deoarece implementările RSA automatizează acest proces, astfel încât nu trebuie să zgâriați niciun număr.

Pro RSA & contra

RSA este unul dintre cei mai susțineți și implementați algoritmi de semnătură digitală, deși există o mișcare către algoritmi mai noi, mai eficienți și mai siguri, precum ECDSA și EdDSA.

În comparație cu DSA (pe care o vom acoperi în secțiunea următoare), RSA este mai rapid la verificarea semnăturilor, dar mai lent la generarea lor. Întrucât semnăturile tind să fie create o dată și verificate de mai multe ori, RSA este în general preferat decât DSA.

DSA

Securitatea algoritmului de semnătură digitală se bazează pe două concepte matematice, problema logaritmului discret și unele proprietăți ale exponenției modulare. Pentru unele grupuri, este imposibil să se calculeze logaritmele lor discrete cu tehnicile și tehnologia actuală.

Generare cheie DSA

Pentru a genera chei DSA, primul pas este alegerea parametrilor pe care un grup de utilizatori din același sistem îl pot utiliza pentru a genera o pereche de chei.

Generarea parametrilor

• Alegerea a funcție hash – SHA-256 este cea mai comună opțiune pentru a satisface cerințele moderne de securitate.
• Stabilirea pe lungimile cheii, L și N – Aceste zile, L ar trebui să aibă cel puțin 2.048 de biți în timp N ar trebui să aibă cel puțin 256 biți.
• Decideți un prim, q, aceasta este aceeași lungime ca și N.
• Selectați un prim, p, Unde p-1 este un multiplu al q.
• Alegeți un număr, g, folosind următoarea formulă (unde h este un număr arbitrar între 1 și p-1):

g = h(p – 1) /q mod p

În mod normal, aceste valori sunt un număr foarte mare pentru a asigura securitatea algoritmului. Pentru a evita ca exemplul nostru să fie prea dificil de calculat sau explicat, vom folosi numere mult mai mici care nu ar fi în realitate sigure. Să spunem că:

    q = 5

    p = 11

A găsi g, ne conectăm numerele în formulă. Noi vom folosi 3 ca valoare pentru h:

g = 3 (11-1) / 5 mod 11

g = 32 mod 11

g = 9 mod 11

Vom folosi același calculator pentru moduloși ca și în Modul de utilizare a cheii private a expeditorului pentru a semna digital valoarea hash secțiune. Parametrii vor fi aceiași, cu excepția:

• Număr A valoare – 9
• Număr b valoare – 11

Dacă ați introdus totul corect, vă va da un rezultat pentru g de 9.

Generarea cheilor de utilizator

Utilizatorii individuali iau apoi acești parametri și îi folosesc pentru a-și forma perechea de chei:

• Cheia privată (X) este un număr între 0 și q, pe care am setat-o ​​la 5. Pentru exemplul nostru, vom alege 2 a fi X, cheia noastră privată.
• Cheia publică (y) se calculează folosind următoarea formulă:

    y = gX mod p

Prin urmare:

y = 92 mod 11

y = 81 mod 11

Vom mai folosi același calculator de modulo încă o dată. Parametrii vor fi aceiași, cu excepția:

• Număr A valoare – 81
• Număr b valoare – 11

Dacă ați introdus lucrurile corect, ar fi trebuit să obțineți un rezultat din y = 4. Prin urmare, cheia publică este 4.

Acum că am generat toate valorile noastre, vă oferim o recapitulare rapidă. Parametrii sistemului sunt:

• p = 11
• q = 5
• g = 9

Perechea noastră de chei este formată din:

• Cheia privată, X = 2
• Cheia publică, y = 4

Semnarea digitală a datelor cu DSA

Expeditorii își pot folosi cheia privată DSA pentru a semna digital datele, care le permite destinatarului să verifice dacă mesajul este autentic și își păstrează integritatea. De asemenea, împiedică expeditorul să poată repudia mesajul.

Procesul de semnătură începe prin generarea unei valori aleatorii k, care este între 1 și q. Pentru acest exemplu, să alegem doar 3 ca număr „aleatoriu”, k.

Urmăm apoi următoarea formulă pentru a crea o cheie individuală (r) pentru mesaj:

r = (gk mod p) mod q

Aruncăm numărul nostru:

r = (93 mod 11) mod 5

r = (729 mod 11) mod 5

Folosim din nou calculatorul modulo, intrând 729 și 11, ceea ce ne oferă un rezultat al 3. Prin urmare:

r = 3 mod 5

Și apoi repetăm ​​din nou operația de modulo cu valorile noi pentru a ne oferi:

r = 3

Valoarea noastră pentru r este folosit ca cheie pentru mesaj.

Venim cu cealaltă parte a semnăturii digitale, s, cu următoarea formulă:

s = k-1(H(m) + xr) mod q

k-1 nu reprezintă preluarea puterii negative a k, ci în schimb calculează inversul modular, la fel ca în cazul nostru Descoperind subsecțiunea cheie privată în partea anterioară a articolului în care am vorbit despre RSA.

H(m) este valoarea hash pentru mesajul pe care expeditorul îl semnează. În mod normal, aceasta ar fi o valoare de hash lungă care a fost derivată din mesaj, la fel ca în Înțelegerea valorilor hash subsecțiunea de mai sus, pe care am tratat-o ​​atunci când vorbim despre algoritmul RSA.

Pentru acest exemplu, vom păstra lucrurile simple. La fel ca în secțiunea RSA, vom spune că mesajul nostru, m, este “Azi e cald“ și că hash-ul mesajului H(m), este 10.

Așadar, să introducem toate valorile noastre în formulă:

s = 3-1 (10 + 2 x 3) (mod 5)

s = 3-1 (10 + 6) (mod 5)

s = 3-1 (16) (mod 5)

Acum, luăm inversul modular al 3 pentru ordinea 5 (deoarece 5 este valoarea noastră pentru q), folosind același calcul invers invers modular de mai devreme. introduce 3 ca număr întreg și 5 ca modulo, care vă va oferi un rezultat de 2. Prin urmare:

s = 2 (16) (mod 5)

s = 32 (mod 5)

Să revenim la calculatorul nostru pentru funcționarea normală a modulului, păstrând aceiași parametri pe care i-am folosit anterior, cu excepția:

• Număr A valoare – 32
• Număr b valoare – 5

Dacă ați făcut acest lucru corect, va oferi o valoare pentru s din 2. Semnătura digitală este compusă din r și s (Respectiv 3 și 2). Expeditorii transmit semnătura digitală destinatarului alături de mesajul lor, „Azi e cald“. De asemenea, vor împărtăși valorile p, q, g și y cu destinatarul lor.

Verificarea semnăturilor digitale

Când destinatarul primește semnătura digitală alături de mesaj, poate verifica integritatea și autenticitatea mesajului cu următorul set de calcule.

Primul pas este de a găsi hash-ul mesajului pe care l-au primit. Destinatarul face acest lucru rulând întregul mesaj printr-o funcție hash. Pentru a păstra lucrurile simple și coerente, să spunem că hașa mesajului, H(m) este 10.

De asemenea, destinatarului i-au fost trimise următoarele valori, pe care le utilizează în procesul de verificare:

• Semnătura digitală (r, s) – 3, 2
• p – 1
• q – 5
• g – 9
• y – 4

Primul calcul este de a găsi w:

w = s-1 mod q

Din nou, s-1 reprezintă luarea inversă modulară. Să introducem valorile noastre:

w = 2-1 mod 5

Vom folosi calculatorul invers modular de mai devreme. introduce 2 ca număr întreg și 5 ca modulo, care vă va oferi un rezultat de 3 pentru w. Următorul pas este să găsești u1 cu următoarea formulă:

u1 = H(m) X w mod q

Aruncăm valorile noastre:

u1 = 10 x 3 mod 5

u1 = 30 mod 5

Înapoi la calculatorul modulului normal, păstrând aceiași parametri pe care i-am folosit anterior, cu excepția:

• Număr A valoare – 30
• Număr b valoare – 5

Acest lucru ne oferă un rezultat al 0 pt u1.

Folosim următoarea formulă pentru a veni cu u2:

u2 = r X w mod q

Să introducem numerele noastre:

u2 = 3 x 3 mod 5

u2 = 9 mod 5

Ne întoarcem apoi către calculatorul modulo normal, folosind aceiași parametri ca mai devreme, cu excepția:

• Număr A valoare – 9
• Număr b valoare – 5

Dacă introduceți corect acest lucru, vă va da un rezultat pentru u2 din 4.

Acum că avem valorile noastre pentru u1 și u2, noi putem gasi v, cu următoarea formulă:

v = (gu1yu2 mod p) mod q

Aruncăm numărul nostru:

v = (90 x 44 mod 11) mod 5

v = (1 x 256 mod 11) mod 5

v = (256 mod 11) mod 5

Revenim la calculatorul nostru modulo normal, folosind aceiași parametri ca mai devreme, cu excepția:

• Număr A valoare – 256
• Număr b valoare – 11

Acest lucru ne oferă un rezultat al 3. Prin urmare:

v = 3 mod 5

Apoi folosim calculatorul modulo normal o dată finală, din nou cu aceiași parametri, cu excepția:

• Număr A valoare – 256
• Număr b valoare – 11

Acest lucru ne oferă un rezultat pentru v din 3.

Dacă mesajul este autentic și nu a fost modificat, atunci v va fi egal cu r:

    v = 3

    r = 3

    3 = 3

Prin urmare, mesajul a fost trimis de către proprietarul cheii private, iar mesajul nu a fost modificat de la semnarea acestuia.

Proza DSA & contra

Securitatea DSA depinde dacă folosește un număr adecvat. Pe lângă p, q și g respectând parametrii corecți, valoarea de k de asemenea, trebuie să fie la întâmplare. Nu trebuie să fie o valoare previzibilă sau o valoare care este folosită de mai multe ori. Dacă aceste cerințe nu sunt îndeplinite, atunci cheia poate fi recuperată de un atacator.

În ciuda acestei posibilități, DSA este în general considerat sigur, atât timp cât este implementat corect și utilizează valori adecvate. Chiar dacă este relativ sigur, DSA nu are tendința de a fi implementat prea mult în comparație cu RSA sau cu celelalte metode de semnătură digitală. În comparație cu RSA, poate genera chei mai rapid și este, de asemenea, mai rapid la generarea de semnături digitale, dar mai lent la verificarea acestora.

Versiunea 7.0 a OpenSSH a încetat să sprijine tastele DSA în mod implicit, ceea ce pare a fi un semn că lumea trece prin DSA și pe alte algoritmi.

ECDSA & EdDSA

RSA și DSA nu sunt singurii algoritmi de semnătură digitală și nici nu sunt cei mai potriviți pentru toate situațiile. Există o serie de altele, cum ar fi ECDSA și EdDSA, care au proprietăți care le fac preferabile în anumite circumstanțe.

Din păcate, acestea se bazează pe o matematică și mai complicată, cum ar fi curba eliptică și criptografia curbei Edwards. Nu le vom acoperi în detaliu astăzi, din cauza acestei complexități adăugate, dar vom vorbi despre unele dintre pozitivele posibile și negative ale acestora..

ECDSA

Algoritmul semnăturii digitale cu curbă eliptică este o variație a DSA care încorporează criptografia curburilor eliptice. Oferă un nivel similar de securitate cu RSA, dar cu o cheie mult mai mică. Acest lucru îl face mai eficient decât RSA sau DSA în cele mai multe aspecte ale performanței.

EdDSA

Aceasta este o altă alternativă DSA, cu excepția faptului că se bazează pe curbele Twisted Edwards. Este relativ nouă în ceea ce privește algoritmii, care are atât avantajele, cât și dezavantajele. Pe partea pozitivă, folosește tehnici mai noi care se adaugă la performanțele sale.

Din păcate, algoritmii mai noi nu au fost expuși la atâtea cercetări, astfel că multe persoane sunt precaute atunci când decid dacă le punem în aplicare sau nu.

În ciuda acestui fapt, utilizarea de EdDSA oferă un nivel înalt de performanță, rezistența la atacurile cu canal lateral și elimină necesitatea unui număr aleatoriu unic în fiecare semnătură. În această etapă, EdDSA pare promițător și începe să vadă o implementare mai largă, dar va trebui să așteptăm și să vedem dacă studiile viitoare vor găsi orificii de securitate.

Certificate digitale

Oricine poate face cu ușurință o pereche de chei, chiar și un atacator. Deci, ceea ce împiedică pe cineva să facă o grămadă de chei și să se prefacă că sunt președintele sau să poarte ca oricine altcineva?

Ei bine, nimic nu împiedică pe cineva să pretindă că este o altă persoană, dar există un sistem în vigoare care le permite celorlalți să constate dacă persoana respectivă este sau nu cine pretinde a fi. Se numește infrastructura cu cheie publică (PKI), și implică certificate digitale care leagă cheia publică a unei persoane sau entități de identitatea reală. Aceste certificate sunt semnate de alții pentru a indica cât de mult trebuie să fie de încredere certificatul.

Puteți compara procesul cu notarii pentru a verifica documentele. Dacă cineva are o copie a unui certificat de naștere, este posibil să fiți sceptici cu privire la faptul dacă este sau nu legitim. Dacă același certificat de naștere a fost semnat și ștampilat de un notar, ai fi mult mai probabil să crezi că este o copie reală.

De ce?

Deoarece semnătura și ștampila arată că o entitate publică de încredere a văzut individul și certificatul de naștere original, atunci a verificat că copia este de fapt legitimă. Notarul validează copia certificatului de naștere și își ia reputația în spatele acesteia cu semnătura și ștampila lor.

Încrederea pe care o avem pentru notar este transferată copiei certificatului de naștere, permițându-ne să avem încredere în ea mult mai mult decât unul care nu a fost notat.

Există două tipuri majore de certificare, cautorități ertificate (CA) și rețeaua de încredere.

Autoritățile de certificare

Autoritățile de certificare sunt organizații de încredere care efectuează verificări asupra unor persoane sau entități pentru a verifica dacă acestea sunt proprietarul legitim al unei chei publice. Dacă verificările dezvăluie că persoana fizică este adevăratul proprietar, atunci autoritatea de certificare va semna certificatul cu propria sa cheie, semnificând că a finalizat verificarea și consideră că cheia individuală și cea publică sunt legitime în mod legitim..

Atâta timp cât avem încredere în autoritatea de certificare și în procesul lor de verificare a cheii, atunci putem avea încredere într-un certificat semnat de acestea, și, astfel, cheia publică reprezintă cu adevărat acel individ.

În funcție de tipul de certificat și de cererea acestuia, nivelurile diferite pot avea diferite procese de verificare și, astfel, reprezintă un grad mai mare sau mai mic de încredere.

Web de încredere

Web-ul de încredere operează sub o premisă similară, cu excepția taici nu există corpuri centrale ca autoritățile de certificare care efectuează procesul de verificare și semnează certificatele.

În schimb, rețeaua de încredere se bazează pe alte persoane pentru a semna certificate, bazându-și reputația pe legătura dintre individ și cheia publică. Acest sistem este folosit mai ales cu PGP, unde utilizatorii își pot face cu ușurință propriile certificate.

Funcționează așa:

Să presupunem că aveți doi prieteni care doresc să fie semnate certificatele lor pentru a demonstra că sunt proprietarii legitimi ai cheilor lor publice. Îi cunoașteți bine pe acești oameni și vă arată codurile lor guvernamentale, ceea ce vă face absolut siguri că sunt cine spun ei și sunt astfel adevărații proprietari ai cheilor publice pe care le solicită..

Întrucât știți că sunt proprietarii legitimi ai cheilor lor publice, sunteți fericiți să utilizați cheia privată pentru a semna certificatele lor, stabilindu-vă reputația asupra lor și spunând în esență „Da, am verificat identitățile acestor persoane și sunt aceia care ei pretind că sunt ”. Acești doi prieteni vă pot face la fel.

Să zicem că fiecare dintre cei doi prieteni ai tăi are alți doi prieteni care doresc ca certificatele lor să fie semnate. Dacă cei doi prieteni semnează aceste alte certificate, atunci puteți utiliza încrederea pe care o aveți în prietenii dvs. pentru a accepta că acești alți oameni sunt cu adevărat cine spun ei că sunt la fel de bine.

Prietenii prietenilor dvs. pot apoi să semneze certificatele persoanelor în care au încredere și așa mai departe, construind în cele din urmă o rețea mare de persoane de încredere. Odată ce aceste site-uri devin suficient de mari și devin interconectate cu alte site-uri, ele pot fi folosite ca mijloc de a avea încredere în oricine altcineva în rețea.

Mai multe semnături pe un certificat, mai ales dacă sunt semnături de la persoane de înaltă încredere, cu atât mai mult poți avea încredere în certificatul digital al cuiva și în legătura dintre cheia publică și identitatea sa.

Utilizatorii PGP dețin frecvent părți cheie de semnare în care oamenii se adună pentru a avea identitatea verificată și certificatele lor digitale semnate. Aceste adunări ajută la aducerea de noi persoane în rețea.

Deși vine cu anumite complexități, avantajul sistemului de încredere este că nu există un corp central care să poată fi corupt.

Semnăturile digitale sunt sigure?

În sens general, Semnăturile digitale sunt sigure, cu excepția cazului în care cheia privată a signeului a fost compromisă. Dacă proprietarul a informat o altă persoană, a lăsat cheia privată scrisă sau a fost furată într-un alt mod, atunci este posibil ca un atacator să semneze digital mesaje ca și cum ar fi proprietarul.

Acest lucru poate duce la atacarea persoanelor care le-ar putea să-și răspundă victima sau să-și modifice datele. Aceasta este o problemă de securitate uriașă și oricine bănuiește că cheia lor a fost compromisă trebuie să-și revoce certificatul digital care le leagă de cheia publică și să aibă unul nou.

Există alte câteva avertismente când vine vorba de securitatea semnăturilor digitale. Ar trebui utilizat un algoritm de semnătură digitală adecvat și trebuie, de asemenea, să fie pus în aplicare în mod corespunzător. Pe lângă aceasta, trebuie să existe și o modalitate de conectare a cheii publice cu proprietarul său, de obicei prin intermediul certificatelor digitale.

Atâta timp cât aceste cerințe sunt îndeplinite, urmați cele mai bune practici din industrie, iar cheia dvs. privată nu a fost compromisă Semnăturile digitale sunt o modalitate excelentă de a oferi autenticitate, integritate și non-repudiere datelor.

Date structurate de Kai Stachowiak autorizat sub CC0