Što su digitalni potpisi i kako funkcioniraju?

Digitalni potpisi slični su elektroničkoj verziji vaših ručno napisanih potpisa. Omogućuju ljudima da provjere stanje autentičnost i cjelovitost podataka, kao i sprečavanje potpisnika u mogućnosti da odbaci (negira) njihovu uključenost.

Ova svojstva dovela su do prihvaćanja digitalnog potpisa u širokom rasponu aplikacija, uključujući mnoge naše sigurnosne protokole, sigurnu e-poštu i upravljanje digitalnim pravima.

U ovom ćemo članku razgovarati što su digitalni potpisi, gdje se koriste, kao i tehničke pojedinosti dvaju najpopularnijih algoritama, RSA i DSA.

Što su digitalni potpisi?

Kao što je gore navedeno, digitalni potpisi pružaju nam tri vrlo važna svojstva. To su provjera autentičnosti, integriteta i nevaljanja.

Ovjera je postupak provjere da je pojedinac koji pošalje poruku uistinu onaj za koga kažu da je, a ne prevarant.

integritet podataka ili se poruka odnosi na to je li stigla u istom stanju kao i kad je poslana. Ako je poruka izmijenjena ili neovlašteno promijenjena, ona više ne zadržava svoju cjelovitost.

Ako su podaci ili poruke non-repudiable, to znači da se njezin autor ne može osporiti da su bili pravi tvorci dokumenta. Ovo svojstvo oduzima vjerojatnu poricanje ili stari izgovor “Oprosti, moj prijatelj je koristio moj račun”.

Sve dok privatni ključ pojedinca nije ugrožen, digitalni potpisi mogu sva tri svojstva dati podatke.

Možda se pitate zašto su nam ova svojstva uopće potrebna. Napravimo korak unatrag i razmislimo o tome kako radimo stvari licem u lice.

Recimo da dugujete prijatelju Mikeu 100 dolara. Dobra si osoba, pa mu rado vraćaš kad dobiješ novac.

Najbolji način da to učinite bio bi samo dati Mikeu novčanicu od 100 USD. Poznavali ste ga godinama i znate kako izgleda, tako bi i bilo lako potvrditi njegov identitet i na taj način potvrditi da novac dajete pravoj osobi.

Ako ste stvarno analni, čak biste mogli provjeriti njegovu osobnu iskaznicu i natjerati ga da potpisuje rukopis za vas. Potpis na primitku dao bi joj cjelovitost i učinio ga nepotkupljivim.

Što ako ako umjesto da izvršite transakciju licem u lice, nazovete nekoga rekavši da je to Mike i da biste trebali poslati 100 USD na broj računa 12345678.

“Ali ne zvučiš kao Mike”, kažeš.

“Prehlađen sam. Pošaljite ga sada, treba mi novac. “

Bi li poslao novac? Vjerojatno ne.

Ne možete znati je li to uistinu Mike ili točan broj računa. Koliko znate, to bi mogao biti prevarant koji pokušava ukrasti od vas. Umjesto da novac odmah prebacite, bilo bi najbolje pričekati dok ne vidite Mikea kako biste mu mogli unovčiti novac osobno.

Baš kao u gornjem scenariju, često nailazimo na situacije u kojima to trebamo provjeriti identitet stranke ili integritet podataka u mrežnom svijetu. Zbog toga su digitalni potpisi postali mehanizam koji može pružiti ova svojstva i olakšati sigurne mrežne transakcije.

Bez njih možda ne možemo znati s kim razgovaramo, ne bismo mogli biti sigurni jesu li podaci krivotvoreni ili ne, i osoba bi mogla poreći da su odgovorni..

Uporaba digitalnog potpisa

Ova svojstva digitalnog potpisa čine ih korisnim u širokom rasponu aplikacija. Oni se često koriste sami ili zajedno s enkripcijom u različitim sigurnosnim protokolima, kao što su:

• IPsec
• SSH
• TLS

Oni se često koriste u upravljanje digitalnim pravima, u blockchain tehnologija, u upravljanje ugovorom aplikacija, kao dio distribucija softvera, i u financije.

Povijest digitalnog potpisa

Ideju o digitalnom potpisu prvi su plasirali poznati kriptografi Whitfield Diffie i Martin Hellman u svom radu iz 1976. godine Novi smjerovi u kriptografiji. 1978. Ronald Rivest, Adi Shamir i Len Adleman doveli su u javni algoritam RSA algoritam koji se može koristiti za proizvodnju nesigurnih digitalnih potpisa.

Prošlo je još jedno desetljeće da se digitalni potpisi pojave u širokoj primjeni: izdanju IBM-ovog Lotus Notes 1.0. Od tada pa nadalje, digitalni potpisi počeli su se širiti usvajanjem kako su se pojavile nove tehnike i potreba za mrežnom provjerom autentičnosti i provjerom integriteta rasla.

Kratki uvod u kriptografiju s javnim ključem

Prije nego što skočimo na digitalni potpis, najbolje je pokriti neke od važnih aspekata kriptografije javnog ključa, koji čine osnovu za funkcioniranje digitalnog potpisa.

Ako ste relativno novi u kriptografiji, sustav koji će vam biti najpoznatiji je šifriranje ključa simetričnog ključa. To samo znači da se isti ključ (koji je sličan lozinci, ali ima neke razlike) koristi i za šifriranje i za dešifriranje podataka.

Šifriranje javnih ključeva bila je revolucija, jer je uključivala pomoću zasebnih ključeva za postupak šifriranja i dešifriranja, što dovodi do niza različitih kriptografskih aplikacija. Ove dvije tipke tvorile su par ključeva, koji se sastojao od javnog i privatnog ključa. Javni se ključ očito može dijeliti javno, dok privatni ključ mora biti čuvan u tajnosti da bi sustav bio siguran.

Dvije najčešće uporabe kriptografije s javnim ključem su šifriranje i digitalni potpis.

Šifriranje

Jedna od najznačajnijih kriptografija javnog ključa bila je ta omogućava strankama koje se nikada nisu susrele da povjerljivo šalju poruke jedna drugoj. Pošiljatelj traži javni ključ željenog primatelja (oni se mogu naći na poslužiteljima javnih ključeva, na osobnim web mjestima ili jednostavno tako da pojedinac zatraži), a zatim šifrira poruku tim ključem prije nego što ga pošalje primatelju..

Primatelj je jedina osoba kojoj može pristupiti poruka – pod pretpostavkom da privatni ključ nije ugrožen – dešifrirajući je svojim privatnim ključem. Iako se za šifriranje poruke koristio javni ključ, on se može dešifrirati samo privatnim ključem. Ako primatelj želi odgovoriti, oni će pronaći javni ključ izvornog pošiljatelja, a zatim ponoviti postupak.

Vidi također: Objašnjene uobičajene vrste šifriranja

Kako rade digitalni potpisi?

Kao što smo rekli, digitalni se potpisi koriste za provjeru autentičnosti, za provjeru jesu li podaci neovlašteni i da se omogući nepotvrđivanje. Postoji niz različitih mehanizama koji se mogu koristiti za digitalni potpis, i svaki od njih ima male varijacije u strukturi strukture.

Općenito, ovi se algoritmi moraju sastojati od tri podagoritma:

• Algoritam stvaranja ključeva – Ovaj algoritam generira slučajni par ključeva za korisnika. Brojevi uključeni u par ključeva moraju se pridržavati određenih parametara da bi se smatrali sigurnim. Dva najvažnija aspekta su da su brojevi dovoljno slučajni i odgovarajuće veličine.
• Algoritam za potpisivanje podataka – Jednom kada korisnik ima svoje ključeve, postoje određeni načini na koji se način primjenjuje na podatke u postupku potpisa.
• Algoritam za provjeru potpisa – Isto tako, provjera potpisa slijedi unaprijed određen postupak.

Da bi sustav digitalnog potpisa bio učinkovit, on mora biti strukturiran na takav način da:

• Podaci potpisani privatnim ključem su potvrđeno odgovarajućim javnim ključem istog pojedinca.
• U osnovi bi bilo nemoguće (koristeći trenutnu tehnologiju i tehnike) krivotvoriti važeći potpis bez poznavanja privatnog ključa pojedinca.

Neke od najčešćih shema digitalnog potpisa uključuju RSA, DSA, EcDSA i EdDSA.

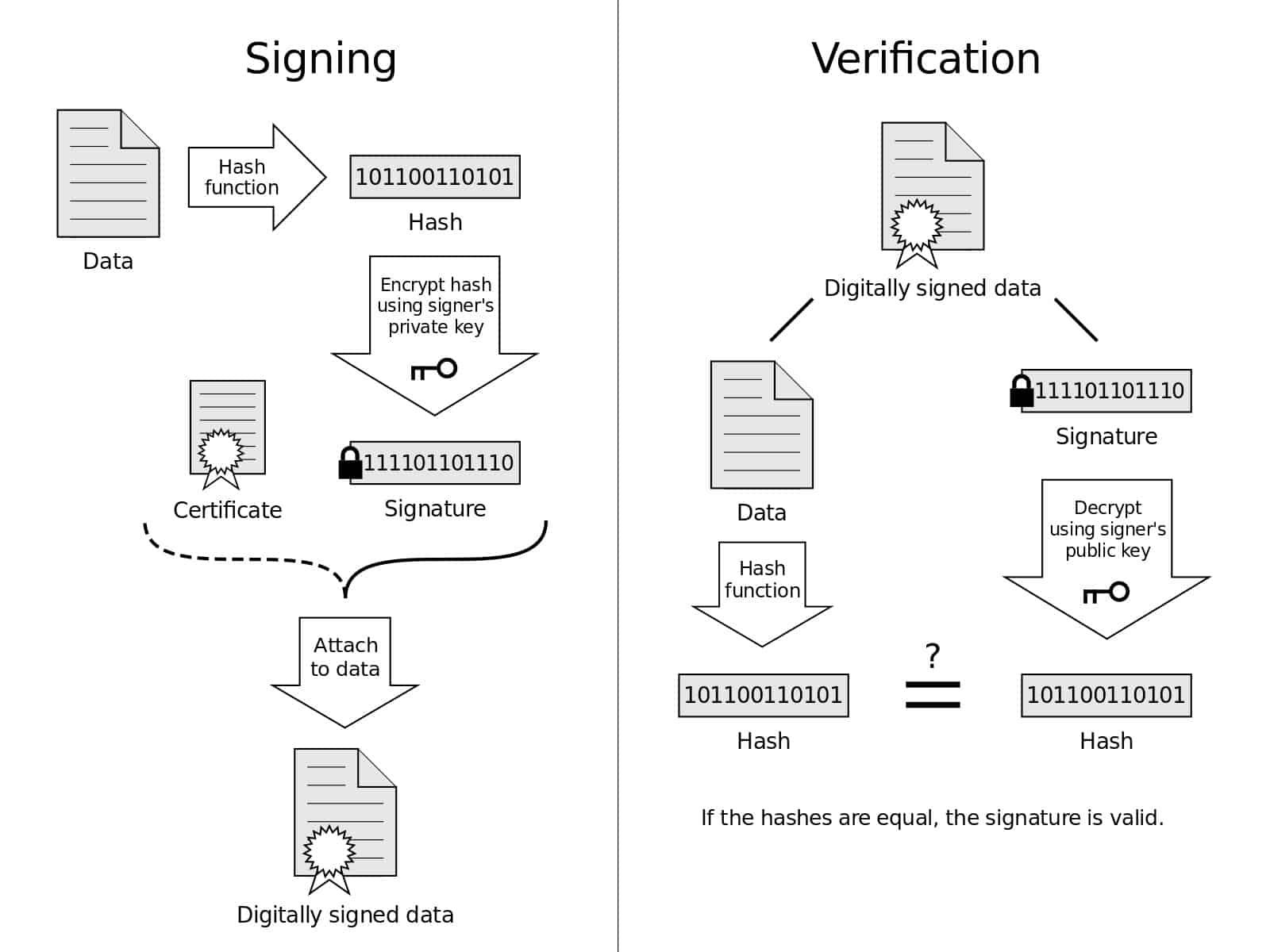
Ova slika daje vizualni prikaz procesa potpisivanja i provjere. Dijagram digitalnog potpisa od Acdx pod licencom pod CC0

RSA

RSA je bio prvi algoritam digitalnog potpisa, ali se također može koristiti za šifriranje javnih ključeva. U ovom ćemo članku preskočiti aspekt šifriranja, ali više o tome možete saznati u našem opsežnom članku koji govori o tome što je RSA i kako funkcionira.

RSA ključna generacija

U sigurnim implementacijama RSA, parovi ključeva obično će se automatski uspostaviti prema sljedećem procesu:

Prime generacija

Odabir su dva pojedinačna glavna broja, p i q. Točna veličina ovih prajmi će se razlikovati ovisno o veličini ključa. Ovih dana općenito se preporučuje najmanje 2048-bitni RSA ključ za adekvatnu sigurnost, pa govorimo o dva glavna broja koji se množe da bi se stvorio 2048-bitni broj.

2048 bita je veličina u sustavu binarnih brojeva. Ako bi se jedan broj ove veličine pretvorio u naš poznatiji decimalni sustav, to bi bio otprilike ovako dug:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

Primeri u RSA moraju biti odabrani nasumično i trebaju imati slične duljine.

U našem primjeru koristit ćemo mnogo manje brojeve kako bismo stvari lakše razumjeli. Imajte na umu da će upotreba tipki ove veličine digitalni potpis učiniti trivijalnim u lažnu. Zbog toga se tako velike vrijednosti koriste u praksi.

Recimo to:

p = 13

q = 17

Prvi korak bio bi izračunavanje modula n koristeći sljedeću formulu:

n = pq

n = 13 x 17

n = 221

Vrijednost n je ujedno i duljina ključa.

Carmichaelova totientska funkcija

Sada kada imamo vrijednost za n, sljedeći je korak upotreba Carmichaelove totientne funkcije:

λ(n) = LCM (p – 1, q – 1)

Nekoliko je stvari koje morate razumjeti:

• λ(n) znači Carmichaelov totient za vrijednost n
• LCM predstavlja najniži zajednički množitelj. To je najniži zajednički broj koji su obojica p-1 i q-1 mogu se podijeliti u

Uključimo naše brojke u jednadžbu:

λ(221) = LCM (13 – 1, 17 – 1)

λ(221) = LCM (12, 16)

Ako ste dobri u mentalnoj matematici, možda ste to shvatili 48 najniži je zajednički množnik obaju 12 i 16. To je zato što je 48 najmanji broj u koji se oba ova broja mogu uklopiti (12 x 4 = 48, 16 x 3 = 48). Stoga:

λ(221) = 48

Spremam se za javni ključ

U RSA-u, javni se ključ sastoji od vrijednosti n (što smo već izračunali kao 221) i e. Budući da se javni ključ slobodno dijeli, vrijednost za e to ne mora biti tajna Zapravo se često postavlja na 65.537 u praksi, jer bi veći broj usporio proces šifriranja. U našem primjeru, postavit ćemo e do 5, samo da bi bio mali i jednostavan broj za rad.

Stoga se javni ključ za ovaj primjer sastoji od 221 i 5. Detalje o načinu na koji se javni ključ primjenjuje obradit ćemo u sljedećim odjeljcima.

Otkrivanje privatnog ključa

Baš kao što se naš javni ključ sastoji od dva broja, tako je i naš privatni ključ. Privatni se ključevi sastoje od d i e. Već znamo vrijednost e (5), a za pronalaženje možemo upotrijebiti sljedeću formulu d:

d = 1 /e modni λ(n)

Primjetite to modni samo simbolizira modulnu operaciju, što bi obično značilo da ostatak morate pronaći nakon što lijevu stranu podijelite s desnom. Kao primjer:

17 mod 3 = 2

To je zato što se 3 uklapaju u 17 ukupno 5 puta, a ostatak 2.

Naš je primjer malo drugačiji. The “1 /e modni”Čini se da se segment jednadžbe govori o podjeli 1 po e, ali to zapravo nije. Zbunjujuće je, ali ovo je način predstavljanja modularni inverzni. Jednadžba nam zapravo govori da izračunamo modularni inverzni broj e i λ(n).

Modularni inverzni se obično izvodi pomoću proširenog euklidskog algoritma, ali to nećemo obuhvatiti u ovom članku. Umjesto toga, samo ćemo koristiti internetski kalkulator kako bismo olakšali stvari.

Sada kada smo to izvukli iz ruke, unesemo svoje vrijednosti u formulu:

d = 1/5 mod 48

Pronaći d, sve što moramo učiniti je unijeti našu vrijednost e (5) u mrežni kalkulator gdje piše broj, tada je naša vrijednost za λ(n), koji je 48, gdje piše modulo.

To nam daje rezultat 29 prema mrežnom kalkulatoru. Stoga će naš privatni ključ činiti:

e = 5

d = 29.

Sada kada smo stvorili oba naša ključa, sljedeće je pitanje: “Što ćemo s njima?” Pa, mogli bismo ih koristiti za šifriranje i dešifriranje poruka kriptografijom javnog ključa, ali ovaj članak govori o digitalnom potpisu, tako da usredotočit ćemo se na to.

Digitalno potpisivanje podataka s RSA-e

Recimo da netko želi poslati poruku svom prijatelju, ali želi biti siguran da prijatelj može provjeriti autentičnost i cjelovitost poruke. To bi mogli učiniti koristeći digitalni potpis RSA za potpis poruke.

Prvi korak je pokrenite cijelu poruku putem hash funkcije. Ovo su jednosmjerne funkcije koje uvijek daju isti izlaz za zadani ulaz. Sigurne hash funkcije u osnovi je nemoguće preokrenuti, što znači da se izlaz ne može upotrijebiti za utvrđivanje ulaza. Također je nemoguće da dvije odvojene poruke imaju isti izlaz.

Više o funkcijama hashna možete pronaći u odjeljku Što je hashing? Odjeljak našeg članka, Šifriranje, hashing, soljenje – u čemu je razlika?

Recimo da želimo digitalno potpisati poruku “Vruće je danas“Tako da naš primatelj može znati je li poruka autentična ili ne i je li bila umiješana. Pa bismo trčali „Vruće je danas“Pomoću hash funkcije.

Razumijevanje hash funkcija

Ovih je dana najčešće korištena sigurna hash funkcija SHA-256. Kada svoju poruku prebacimo putem internetskog kalkulatora SHA-256, ona daje rezultat poput ovog:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

Ovo stvara nekoliko problema za naš primjer. Prvi je da to nije decimalni broj poput onoga na koji je većina ljudi navikla. Možda ste primijetili da u ovom broju postoje slova i da se samo oni popeju na njih f. To nam daje pojma da je ustvari heksadecimalni broj.

šesterokutni sustav temelji se na bazi 16, a ne na bazi 10, poput brojačkog sistema koji inače koristimo. To znači da se, umjesto da se broji u množini od 10, broji u množini od 16, a prvih 6 slova naše abecede koriste se za izradu tih dodatnih brojeva. Broj poput ovog može se pretvoriti u naš svakodnevni decimalni sustav, ali to je izvan okvira ovog članka.

Drugo pitanje koje imamo jest da se radi o zaista velikom broju. Ako bi se pretvorio u decimalnu vrijednost bio bi još duži. Budući da smo u ovom vodiču ciljani na jednostavnost, pokretanje izračuna s tako velikim brojem učinilo bi stvari previše zbunjujućim da bi se dobili osnovni pojmovi u cijelosti.

S idejom da pokažemo kako RSA digitalni potpisi funkcioniraju na jednostavan način, nećemo upotrebljavati tako veliku hash vrijednost u sljedećem primjeru. Umjesto toga, pravit ćemo se da je hash vrijednost “Vruće je danas“Jednostavno je 10.

Također ćemo se morati pretvarati da će, poput bilo kojeg pravog hash-a, kad god stavimo svoj unos “Danas je vruće” kroz hash funkciju, uvijek vraća vrijednost 10. Da bismo bili u skladu s načinom funkcioniranja hash funkcija, morat ćemo se pretvarati da je nevjerojatno malo da će bilo koji drugi ulaz dati istu vrijednost. Slično tome, moramo se pretvarati da iz ove vrijednosti također nije izvedivo naš izvorni unos. Ova svojstva su ono što hašiš čini izuzetno korisnim.

Kako se privatni ključ pošiljatelja koristi za digitalno potpisivanje hash vrijednosti

Naš pošiljatelj je upisao njihovu poruku, a zatim je poslao pomoću hash funkcije, za koju pretvaramo da je vratila vrijednost 10. Nakon što pošiljatelj ima hash poruke, može stvoriti digitalni potpis primjenom privatnog ključa na hash vrijednost sa sljedećom formulom:

m (c) = cd modni n

Ovo je zapravo formula za dešifriranje podataka koji su šifrirani javnim ključem primatelja, ali se također koriste za digitalno potpisivanje dokumenata.

Kada je riječ o digitalnom potpisu:

• Vrijednost m (c) bit će potpis.
• Vrijednost c je hash poruke (10).
• Vrijednost d je dio pošiljateljevog privatnog ključa, koji smo prethodno izvadili (29).
• modni funkcija je ista preostala operacija koju smo prethodno pokrili.
• Vrijednost n je drugi dio privatnog ključa pošiljatelja, koji smo izračunali na početku (221).

Pa, stavimo to sve u našu formulu:

m (c) = 1029 mod 221

    m (c) = 100.000.000.000.000.000.000.000.000 mod 221

Pokrenimo to putem sljedećeg modula kalkulatora (objasnili smo kako ove operacije rade u okviru Utvrđivanje javnog ključa odjeljak). Da bi on pravilno radio, moramo svoje ulaze postaviti na:

• Broj vrsta – decimal
• Broj vrijednost – 100000000000000000000000000000
• Broj b vrsta – decimal
• Broj b vrijednost – 221
• Jednadžba izračunavanja (ovo je samo kôd koji kalendaru govori koja operacija treba obavljati. Ovaj i ostali kodovi mogu se naći na web stranici povezanoj iznad ulaznog odjeljka) – mod (a, b)

Ako ste ispravno postupili, to bi trebalo izgledati ovako:

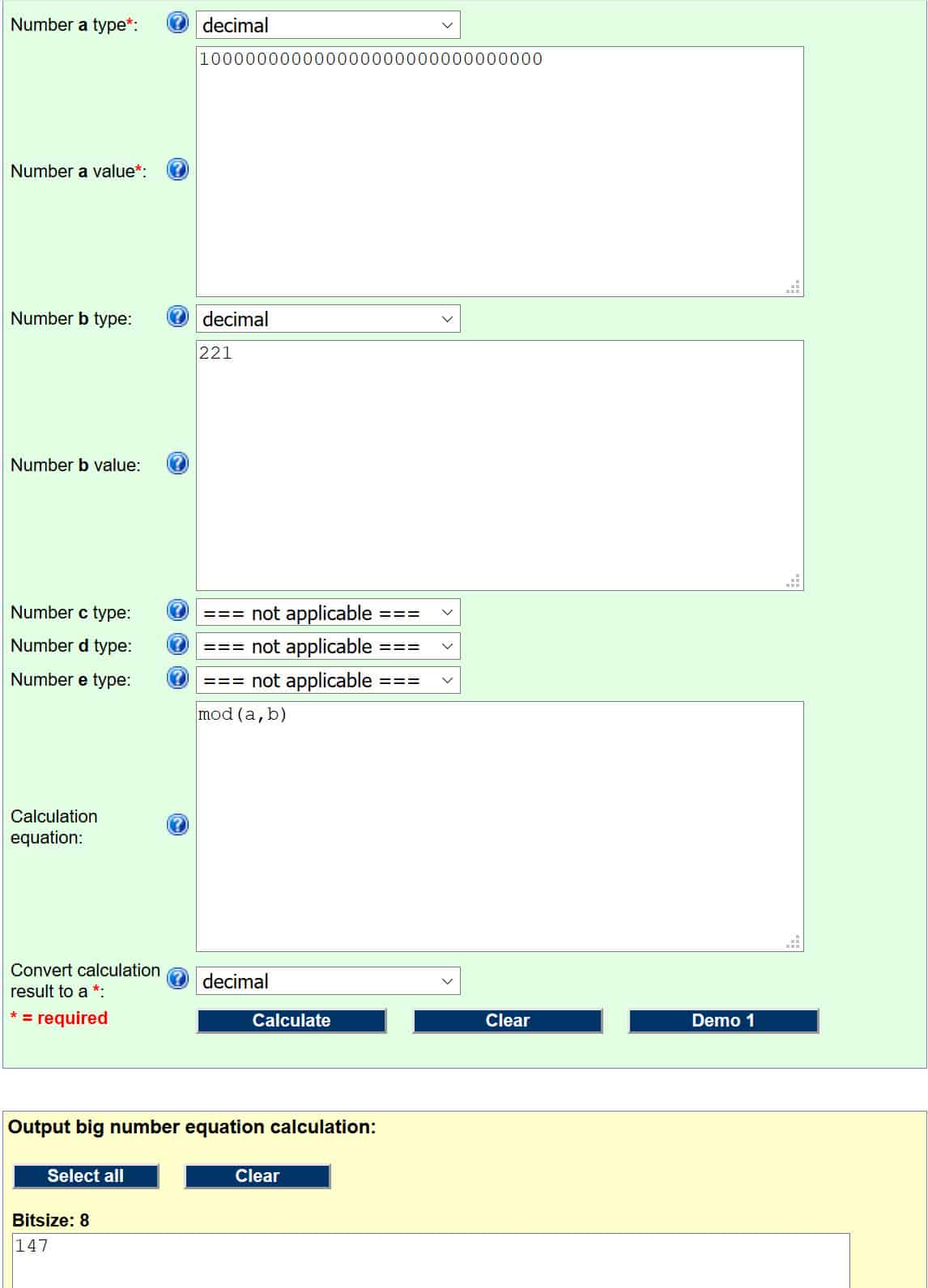
Broj u žutom polju naš je odgovor, pa je digitalni potpis za hash poruke 147.

Da bismo dokazali autentičnost i cjelovitost poruke, zajedno s pružanjem nepotvrđivanja, naš je pošiljatelj prenio poruku „Vruće je danas“, Uz digitalni potpis tvrtke 147 željenom primatelju. Sjetite se samo da smo koristili malu vrijednost za hash da bismo pojednostavili stvari, umjesto pravog hash-a poruke.

Provjera digitalnih potpisa

Digitalni potpisi korisni su samo ako možemo provjeriti jesu li legitimni. Sve dok privatni ključ pošiljatelja nije ugrožen, primatelj može provjeriti je li poruka autentična i zadržava li svoj integritet primjenom sljedeće digitalne potpisa na sljedeću formulu:

    c (m) = me modni n

U preokretu procesa potpisivanja, ovo je zapravo formula koja se koristi za šifriranje podataka u RSA. Kad koristimo ovu formulu za provjeru potpisa:

• Vrijednost c (m) bit će pošiljateljeva hash vrijednost u trenutku kada su ga potpisali (zbog strukture algoritma RSA javnog ključa, primjena pošiljateljevog javnog ključa putem ove formule ponistit će operaciju potpisivanja koju smo upravo izveli, ostavivši nas sa svojim izvornim hash pretvaranjem ).
• Vrijednost m je digitalni potpis (147).
• Vrijednost e je dio javnog ključa pošiljatelja, koji smo izvadili ranije (5).
• modni funkcija je ista preostala operacija koju smo prethodno pokrili.
• Vrijednost n je drugi dio javnog ključa pošiljatelja, koji smo izračunali na početku (221).

Ubacimo sve to u formulu:

    c (m) = 1475 mod 221

    c (m) = 68.641.485.507 mod 221

Upotrijebimo isti modulski kalkulator kao i prije i zadržite sve isto, osim:

• Broj vrijednost – 68641485507

Ako ste ispravno unijeli stvari, trebali biste dobiti rezultat:

c (m) = 10

Sada kada je primatelj izračunao hash vrijednost iz digitalnog potpisa, njihov je sljedeći korak izračunavanje hash vrijednosti poruke koju je primio, “Vruće je danas”. Ako se sjećate iz ranije, zapravo nismo koristili pravi SHA-256 hash poruke, jer bi taj broj bio prevelik i napravio primjer previše složenim.

Umjesto toga, pretvarali smo se da nam je zapravo hash funkcija dala mali broj, 10, za naš doprinos. Budući da hash funkcije uvijek daju isti rezultat za dani unos, kad naš primatelj postavi “Vruće je danas“Pomoću naše imaginarne hash funkcije oni bi također dobili vrijednost 10.

Proces provjere potpisa ima dvije vrijednosti. Prva vrijednost je hash kakav je bio kad ga je pošiljatelj digitalno potpisao svojim privatnim ključem. Gore smo izračunali koristeći javni ključ pošiljatelja.

Druga vrijednost je hash poruke koju je primatelj primio. To se izračunava pomoću iste hash funkcije koju je pošiljalac upotrijebio za pisanje izvorne poruke. Te dvije vrijednosti se zatim uspoređuju, a ako su vrijednosti iste, tada možemo pretpostaviti da je poruka autentična, da zadržava svoj integritet i da se ne može ponoviti. Naravno, ovo pretpostavlja da privatni ključ pošiljatelja nije ugrožen.

Budući da je naš primjer vratio vrijednost od 10 za hash kada ga je potpisao pošiljatelj, kao i vrijednost od 10 kao hash poruke koja je primljena, možemo pretpostaviti da je poruka, “Vruće je danas” dolazi od osobe koja tvrdi da ga je poslala i da nije promijenjena otkad je poslana.

Ako primatelj želi odgovoriti tako da njihov dopisnik može potvrditi njihovu poruku na isti način, cijeli se postupak ponavlja, osim što se privatni i javni ključevi primatelja koriste za postupke potpisivanja i provjere..

Sva ta matematika možda vas je odvratila od čitave ideje o digitalnom potpisu. Ne brinite, jer implementacije RSA automatiziraju ovaj postupak, tako da ne morate krčiti nijedan broj.

RSA pro & kontra

RSA je jedan od najčešće podržanih i implementiranih algoritama digitalnog potpisa, iako postoji pomak prema novijim, učinkovitijim i sigurnijim algoritmima kao što su ECDSA i EdDSA.

U usporedbi s DSA-om (koji ćemo opisati u sljedećem odjeljku), RSA je brži u provjeri potpisa, ali sporiji pri njihovom generiranju. Budući da se potpisi stvaraju jednom i provjeravaju više puta, RSA se uglavnom preferira nad DSA.

DSA

Sigurnost algoritma digitalnog potpisa temelji se na dva matematička koncepta, diskretnom problemu logaritma i nekim svojstvima modularne eksponencije. Za neke su skupine nemoguće izračunati njihove diskretne logaritme trenutnim tehnikama i tehnologijom.

DSA generacija ključeva

Da biste generirali DSA ključeve, prvi korak je odabir parametara koje grupa korisnika u istom sustavu može upotrijebiti za generiranje parova ključeva.

Generiranje parametara

• Odabir a hash funkcija – SHA-256 je najčešća opcija za ispunjavanje modernih sigurnosnih zahtjeva.
• Postavljanje na duljine ključeva, L i N – Ovih dana, L trebao bi biti najmanje 2.048 bita, dok N trebao bi biti najmanje 256 bita.
• Odlučite se za premijeru, q, to je iste dužine kao N.
• Odaberite premijeru, p, gdje p-1 je višestruki od q.
• Odaberite broj, g, pomoću sljedeće formule (gdje h je proizvoljni broj između 1 i p-1):

g = h(p – 1) /q modni p

Obično su te vrijednosti vrlo velike brojke kako bi se algoritam mogao osigurati. Da se naš primjer ne bi previše teško izračunati ili objasniti, upotrijebit ćemo mnogo manje brojeve koji zapravo ne bi bili sigurni. Recimo to:

    q = 5

    p = 11

Pronaći g, ubacujemo svoje brojeve u formulu. Iskoristit ćemo 3 kao našu vrijednost za h:

g = 3 (11-1) / 5 mod 11

g = 32 mod 11

g = 9 mod 11

Upotrijebit ćemo isti kalkulator modula kao i na Kako se privatni ključ pošiljatelja koristi za digitalno potpisivanje hash vrijednosti odjeljak. Parametri će biti isti, osim:

• Broj vrijednost – 9
• Broj b vrijednost – 11

Ako ste sve ispravno unijeli, to će vam dati rezultat za g od 9.

Generiranje korisničkih ključeva

Potom pojedini korisnici uzimaju ove parametre i koriste ih za oblikovanje svog ključnog para:

• Privatni ključ (x) je broj između 0 i q, koju smo postavili na 5. Za naš primjer odabrat ćemo 2 biti x, naš privatni ključ.
• Javni ključ (y) izračunava se prema sljedećoj formuli:

    y = gx modni p

Stoga:

y = 92 mod 11

y = 81 mod 11

Upotrijebit ćemo isti kalkulator modula još jednom. Parametri će biti isti, osim:

• Broj vrijednost – 81
• Broj b vrijednost – 11

Ako ste ispravno upisali stvari, trebali ste dobiti rezultat y = 4. Javni ključ je, dakle 4.

Sada kada smo stvorili sve naše vrijednosti, dajmo vam kratki sažetak. Parametri za sustav su:

• p = 11
• q = 5
• g = 9

Naš ključni par čine:

• Privatni ključ, x = 2
• Javni ključ, y = 4

Digitalno potpisivanje podataka pomoću DSA

Pošiljatelji mogu koristiti svoj DSA privatni ključ za digitalno potpisivanje podataka, što omogućava njihovom primatelju da provjeri je li poruka autentična i zadržava li svoj integritet. Također sprečava pošiljatelja da može odbiti poruku.

Proces potpisa počinje generiranjem slučajne vrijednosti k, koja je između 1 i q. Za ovaj primjer, samo odaberite 3 kao naš “slučajni” broj, k.

Zatim slijedimo sljedeću formulu za stvaranje pojedinačnog ključa (r) za poruku:

r = (gk modni p) mod q

Uključimo u naše brojeve:

r = (93 mod 11) mod 5

r = (729 mod 11) mod 5

Ponovno koristimo naš modulski kalkulator, ulazi 729 i 11, što nam daje rezultat od 3. Stoga:

r = 3 mod 5

A onda opet ponovimo modul operaciju s novim vrijednostima koje će nam dati:

r = 3

Naša vrijednost za r koristi se kao ključ za poruku.

Smislimo drugi dio digitalnog potpisa, a, sa sljedećom formulom:

a = k-1(H(m) + XR) mod q

k-1 ne predstavlja uzimanje negativne moći k, ali umjesto da se izračuna modularni inverzni, baš kao i u našem Izračunavanje potpoglavlja privatnog ključa u ranijem dijelu članka u kojem smo govorili o RSA.

H(m) je vrijednost hash-a za poruku koju pošiljalac potpisuje. Obično bi to bila duga hash vrijednost koja je izvedena iz poruke, baš kao i u Razumijevanje hash vrijednosti pododjeljak gore, koji smo pokrivali kada smo govorili o algoritmu RSA.

Za ovaj primjer pojednostavit ćemo stvari. Baš kao u odjeljku RSA, reći ćemo da je naša poruka, m, je „Vruće je danas” i da je hash poruke H(m), iznosi 10.

Pa, unesemo sve naše vrijednosti u formulu:

a = 3-1 (10 + 2 x 3) (mod 5)

a = 3-1 (10 + 6) (mod 5)

a = 3-1 (16) (mod 5)

Sada uzmemo modularni obratni oblik 3 za naredbu od 5 (jer 5 je naša vrijednost za q), koristeći isti modularni inverzni kalkulator od ranije. Unesi 3 kao cijeli broj i 5 kao modul koji će vam dati rezultat od 2. Stoga:

a = 2 (16) (mod 5)

a = 32 (mod 5)

Vratimo se našem kalkulatoru za normalan rad modula zadržavajući iste parametre kao i ranije, osim:

• Broj vrijednost – 32
• Broj b vrijednost – 5

Ako ste to učinili ispravno, dat će vrijednost za a od 2. Digitalni potpis sastoji se od r i a (3 i 2, respektivno). Pošiljatelji prenose primatelju digitalni potpis zajedno s porukom, “Vruće je danas”. Oni će također dijeliti vrijednosti p, q, g i y sa svojim primateljem.

Provjera digitalnih potpisa

Kad primatelj primi digitalni potpis uz poruku, može potvrditi integritet i autentičnost poruke slijedeći skup izračuna.

Prvi korak je pronalazak hash-a poruke koju su primili. Primatelj to čini pokretanjem cijele poruke putem hash funkcije. Da bi stvari bile jednostavne i dosljedne, recimo da je sloj poruke, H(m) iznosi 10.

Primatelju su također poslane sljedeće vrijednosti koje koriste u postupku provjere:

• Digitalni potpis (r, s) – 3, 2
• p – 1
• q – 5
• g – 9
• y – 4

Prvi izračun je pronaći w:

w = a-1 mod q

Opet a-1 predstavlja uzimanje modularnog obrnutog. Unesite naše vrijednosti:

w = 2-1 mod 5

Koristit ćemo modularni inverzni kalkulator od ranije. Unesi 2 kao cijeli broj i 5 kao modul koji će vam dati rezultat od 3 za w. Sljedeći korak je pronaći u1 sa sljedećom formulom:

u1 = H(m) x w modni q

Ubacimo u naše vrijednosti:

u1 = 10 x 3 mod 5

u1 = 30 mod 5

Vratite se uobičajenom kalkulatoru modula zadržavajući iste parametre kao i ranije, osim:

• Broj vrijednost – 30
• Broj b vrijednost – 5

To nam daje rezultat 0 for u1.

Sljedeću formulu koristimo u2:

u2 = r x w modni q

Unesite naše brojeve:

u2 = 3 x 3 mod 5

u2 = 9 mod 5

Vratimo se na uobičajeni modulski kalkulator koristeći iste parametre kao i ranije, osim:

• Broj vrijednost – 9
• Broj b vrijednost – 5

Ako to ispravno unesete, dobit će rezultat za u2 od 4.

Sad kad imamo svoje vrijednosti za u1 i u2, možemo pronaći v, sa sljedećom formulom:

v = (gu1yu2 modni p) mod q

Uključimo u naše brojeve:

v = (90 x 44 mod 11) mod 5

v = (1 x 256 mod 11) mod 5

v = (256 mod 11) mod 5

Vratimo se našem uobičajenom kalkulatoru modula koristeći iste parametre kao i ranije, osim:

• Broj vrijednost – 256
• Broj b vrijednost – 11

To nam daje rezultat 3. Stoga:

v = 3 mod 5

Tada koristimo normalan kalkulator modula jedan završni put, opet s istim parametrima, osim:

• Broj vrijednost – 256
• Broj b vrijednost – 11

To nam daje rezultat za v od 3.

Ako je poruka autentična i nije krivotvorena, tada v će biti jednak r:

    v = 3

    r = 3

    3 = 3

Stoga je poruku poslao vlasnik privatnog ključa, a poruka nije promijenjena otkako je potpisana.

DSA profesionalci & kontra

Sigurnost DSA ovisi o tome koristi li on odgovarajuće brojeve. Pored toga p, q i g pridržavajući se ispravnih parametara, vrijednost k također mora biti slučajna. To ne bi trebala biti predvidljiva vrijednost ili vrijednost koja se koristi više puta. Ako ti zahtjevi nisu ispunjeni, napadač može otkriti ključ.

Unatoč toj mogućnosti, DSA se općenito smatra sigurnim ako je pravilno implementiran i koristi adekvatne vrijednosti. Iako je relativno siguran, DSA se ne nastoji primijeniti mnogo u usporedbi s RSA-om ili drugim metodama digitalnog potpisa. U usporedbi s RSA-om, ključevi mogu generirati brže i brže je generirati digitalne potpise, ali sporije pri provjeri..

Verzija 7.0 OpenSSH je zadano prestala podržavati DSA ključeve, što se čini znakom da se svijet kreće mimo DSA-e i prema drugim algoritmima.

ECDSA & EdDSA

RSA i DSA nisu jedini algoritam digitalnog potpisa, niti su najprikladniji za sve situacije. Postoji niz drugih, kao što su ECDSA i EdDSA, koja imaju svojstva koja im u određenim okolnostima čine prednost.

Nažalost, oni se oslanjaju na još složeniju matematiku, kao što su eliptična krivulja i kriptografija Edwardsove krivulje. Nećemo ih danas detaljno pokrivati ​​zbog dodane složenosti, ali govorit ćemo o nekim njihovim potencijalnim pozitivnim i negativnim stvarima.

ECDSA

Algoritam digitalnog potpisa Elliptic Curve je inačica DSA koja uključuje kriptografiju eliptične krivulje. Pruža sličnu razinu sigurnosti kao RSA, ali s puno manjim tipkama. To ga čini učinkovitijim od RSA ili DSA u većini aspekata performansi.

EdDSA

Ovo je još jedna alternativa DSA, osim što se temelji na krivuljama Twisted Edwards. Relativno je nov što se tiče algoritama, što ima i svoje prednosti i nedostatke. S pozitivne strane, koristi se novijim tehnikama koje pridonose njezinoj izvedbi.

Nažalost, noviji algoritmi nisu izloženi toliko pomno ispitivanju, pa su mnogi oprezni kad odlučuju hoće li ih primijeniti ili ne..

Unatoč tome, upotreba EdDSA pruža visoku razinu performansi, otpornost na napade bočnih kanala i uklanja potrebu za jedinstvenim slučajnim brojem u svakom potpisu. U ovoj fazi EdDSA izgleda obećavajuće i počinje vidjeti širu implementaciju, ali morat ćemo pričekati i vidjeti hoće li buduće studije pronaći rupe u sigurnosti.

Digitalni certifikati

Svatko može lako stvoriti par ključeva, čak i napadač. Pa što sprečava nekoga da napravi gomilu ključeva i pretvara se da je predsjednik ili da se predstavlja kao bilo tko drugi?

Pa, ništa ne sprečava nekoga da tvrdi da je druga osoba, ali postoji sustav koji omogućava drugima da utvrde je li osoba uistinu ona za koju tvrde da je ili ne. Zove se infrastruktura javnog ključa (PKI), a uključuje digitalne potvrde koje povezuju javni ključ pojedinca ili entiteta s njihovim stvarnim identitetom. Ove potvrde potpisuju drugi kako bi se pokazalo koliko treba vjerovati certifikatu.

Postupak možete usporediti s korištenjem javnih bilježnika za provjeru dokumenata. Ako netko ima kopiju izvoda iz matične knjige rođenih, možda ćete biti skeptični u pogledu toga da li je zakonit ili ne. Ako je isti taj rodni list potpisao i ovjerio notar, vjerovatnije bi bilo vjerovati da je to stvarna kopija.

Zašto?

Budući da potpis i pečat pokazuju da je javni subjekt od povjerenja vidio pojedinca i njegov izvorni izvod iz matične knjige rođenih, tada je potvrdio da je kopija u stvari zakonita. Javni bilježnik ovjerava presliku izvoda iz matične knjige rođenih i za to stavlja svoj ugled svojim potpisom i pečatom.

Povjerenje koje imamo za bilježnika prelazi u kopiju izvoda iz matične knjige rođenih, omogućavajući nam da vjerujemo daleko više od onoga koji nije ovjeren..

Postoje dvije glavne vrste certifikacije, cpotvrđuju nadležna tijela (CA) i mrežu povjerenja.

Tijela za ovjeru

Tijela za ovjeru su pouzdane organizacije koje vrše provjere pojedinaca ili entiteta kako bi provjerile jesu li legitimni vlasnik javnog ključa. Ako provjere otkriju da je pojedinac pravi vlasnik, tijelo za ovjeru potpisat će potvrdu vlastitim ključem, što znači da je provjeru izvršio i vjeruje da su pojedinačni i javni ključ legitimno povezani.

Sve dok vjerujemo autoritetu certifikata i njegovom postupku provjere ključa, tada možemo vjerovati certifikatu koji je on potpisao, i time javni ključ zaista predstavlja tog pojedinca.

Ovisno o vrsti certifikata i njegovoj primjeni, različite razine mogu imati različite postupke provjere, pa tako predstavljaju ili viši ili niži stupanj povjerenja.

Mreža povjerenja

Web povjerenja djeluje u sličnoj premisi, osim tovdje nema središnjih tijela poput certifikacijskih tijela koja provode postupak provjere i potpisuju certifikate.

Umjesto toga, mreža povjerenja oslanja se na druge pojedince da potpišu potvrde, stavljajući svoju reputaciju na vezu između pojedinca i javnog ključa. Ovaj se sistem uglavnom koristi s PGP-om, gdje korisnici lako mogu dati vlastite certifikate.

Djeluje ovako:

Recimo da imate dva prijatelja koji žele da im se potvrde potpišu da dokazuju da su legitimni vlasnici svojih javnih ključeva. Te ljude dobro poznajete i pokazuju vam vladine iskaznice, zbog čega ste apsolutno sigurni da su oni oni za koje kažu da su, i samim tim su istinski vlasnici javnih ključeva za koje tvrde..

Budući da znate da su oni legitimni vlasnici njihovih javnih ključeva, rado koristite svoj privatni ključ za potpisivanje njihovih potvrda, ulažući im vašu reputaciju i u osnovi kažete “Da, potvrdio sam identitet tih pojedinaca i oni su koji tvrde da jesu “. Ova dva prijatelja tada mogu učiniti isto i vama.

Recimo da svaki od vaša dva prijatelja ima još dva prijatelja koji žele svoje potpise. Ako vaša dva prijatelja potpišu ove druge potvrde, tada možete upotrijebiti povjerenje svojih prijatelja da biste prihvatili da su ti drugi ljudi zaista oni koji kažu da jesu..

Prijatelji vaših prijatelja tada mogu potpisati potvrde ljudi u koje imaju povjerenja i tako dalje, naposljetku gradeći veliku mrežu pojedinaca u koje imaju povjerenja. Jednom kada ovi mrežari postanu dovoljno veliki i postaju povezani s drugim mrežama, mogu se koristiti kao sredstvo za povjerenje bilo kome drugom u mreži.

Što više potpisa na certifikatu, pogotovo ako se radi o potpisima osoba s puno povjerenja, što više možete vjerovati nečijem digitalnom certifikatu i vezi između njegovog javnog ključa i njegovog identiteta.

Korisnici PGP-a često održavaju ključne potpise na kojima se ljudi okupljaju kako bi provjerili svoj identitet i potpisali svoje digitalne potvrde. Ova druženja pomažu prikupljanju novih ljudi u mreži.

Iako dolazi s nekim složenjima, prednost web sustava povjerenja je ta što ne postoji središnje tijelo koje se može pokvariti.

Jesu li digitalni potpisi sigurni?

U općem smislu, digitalni su potpisi sigurni osim ako privatni ključ primatelja nije ugrožen. Ako je vlasnik obavijestio drugu osobu, ostavio privatni ključ zapisan ili ga je ukrao na drugi način, tada je napadač mogao digitalno potpisati poruke kao da je on vlasnik.

Ovo može dovesti do toga da napadač lažno predstavlja svoju žrtvu ili neovlašteno dira u njihove podatke. Ovo je veliki sigurnosni problem, a svi koji sumnjaju da je njihov ključ ugrožen, moraju opozvati svoju digitalnu potvrdu koja ih povezuje s njihovim javnim ključem i izdati novi.

Postoji nekoliko drugih upozorenja kada je u pitanju sigurnost digitalnog potpisa. Treba koristiti odgovarajući algoritam digitalnog potpisa, a također ga treba pravilno implementirati. Pored toga, također mora postojati i način povezivanja javnog ključa s njegovim vlasnikom, obično putem digitalnih certifikata.

Sve dok su ti zahtjevi zadovoljeni, slijedite najbolje industrijske prakse i vaš privatni ključ tada nije ugrožen digitalni potpisi izvrstan su način za pružanje autentičnosti, integriteta i nepotvrđivanja podataka.

Strukturirani podaci autor Kai Stachowiak pod licencom pod CC0