ลายเซ็นดิจิทัลคืออะไรและทำงานอย่างไร

ลายเซ็นดิจิทัลเป็นเหมือนลายมือชื่ออิเล็กทรอนิกส์ของคุณในรูปแบบอิเล็กทรอนิกส์ พวกเขาอนุญาตให้คนตรวจสอบ ความถูกต้องและความสมบูรณ์ของข้อมูล, เช่นเดียวกับการป้องกันไม่ให้ผู้ลงนามสามารถปฏิเสธ (ปฏิเสธ) การมีส่วนร่วมของพวกเขา.

คุณสมบัติเหล่านี้นำไปสู่การยอมรับลายเซ็นดิจิทัลในแอปพลิเคชันที่หลากหลายรวมถึงโปรโตคอลความปลอดภัยของเราอีเมลที่ปลอดภัยและในการจัดการสิทธิ์ดิจิทัล.

ในบทความนี้เราจะพูดถึง ลายเซ็นดิจิทัลคืออะไร, พวกเขาจะใช้ที่ใดรวมถึงรายละเอียดทางเทคนิคของอัลกอริทึมยอดนิยมสองอย่าง, RSA และ DSA.

ลายเซ็นดิจิทัลคืออะไร?

ตามที่ระบุไว้ข้างต้นลายเซ็นดิจิทัลมอบคุณสมบัติที่สำคัญสามประการแก่เรา เหล่านี้คือการรับรองความถูกต้องความสมบูรณ์และไม่ปฏิเสธ.

การรับรอง เป็นกระบวนการในการตรวจสอบว่าบุคคลที่ส่งข้อความนั้นเป็นใครจริงๆพวกเขาบอกว่าพวกเขาเป็นและไม่ได้เป็นคนหลอกลวง.

ความสมบูรณ์ ข้อมูลหรือข้อความอ้างอิงถึงว่ามันมาถึงในสถานะเดียวกับเมื่อมันถูกส่ง หากข้อความมีการเปลี่ยนแปลงหรือถูกดัดแปลงข้อความนั้นจะไม่คงอยู่ในความถูกต้องอีกต่อไป.

หากข้อมูลหรือข้อความเป็น ไม่ใช่ repudiable, หมายความว่าผู้แต่งไม่สามารถโต้แย้งได้ว่าพวกเขาเป็นผู้สร้างที่แท้จริงของเอกสาร สถานที่ให้บริการนี้นำไปสู่การปฏิเสธความน่าเชื่อถือหรือข้ออ้าง“ ขออภัยเพื่อนของฉันใช้บัญชีของฉัน”.

ตราบใดที่คีย์ส่วนตัวของแต่ละบุคคลไม่ได้ถูกบุกรุกลายเซ็นดิจิทัลสามารถให้คุณสมบัติทั้งสามนี้แก่ข้อมูล.

คุณอาจสงสัยว่าทำไมเราถึงต้องการคุณสมบัติเหล่านี้ตั้งแต่แรก ลองย้อนกลับไปและคิดเกี่ยวกับวิธีที่เราทำสิ่งต่าง ๆ ในการเผชิญหน้าแบบเผชิญหน้า.

สมมติว่าคุณเป็นหนี้ Mike $ เพื่อนของคุณ คุณเป็นคนดีดังนั้นคุณยินดีที่จะจ่ายคืนให้เขาเมื่อคุณได้รับเงิน.

วิธีที่ดีที่สุดที่จะทำคือเพียงแค่ให้เงิน $ 100 กับไมค์ คุณรู้จักเขามาหลายปีแล้วและรู้ว่าเขาเป็นอย่างไรดังนั้นมันจะเป็นเช่นนั้น ง่ายต่อการตรวจสอบตัวตนของเขาและทำให้รับรองว่าคุณให้เงินแก่คนที่เหมาะสม.

หากคุณทวารหนักจริงๆคุณสามารถตรวจสอบ ID ของเขาและทำให้เขาเซ็นใบเสร็จด้วยลายมือให้คุณ. ลายเซ็นบนใบเสร็จรับเงินจะให้ความซื่อสัตย์และทำให้มันไม่สามารถปฏิเสธได้.

จะทำอย่างไรถ้าแทนที่จะทำธุรกรรมแบบเห็นหน้ากันคุณจะได้รับโทรศัพท์จากคนที่บอกว่าพวกเขาเป็น Mike และคุณควรส่ง $ 100 ไปที่หมายเลขบัญชี 12345678.

“ แต่คุณไม่ฟังเหมือนไมค์” คุณพูด.

“ ฉันเป็นหวัด ส่งทันทีฉันต้องการเงิน”

คุณจะส่งเงินได้ไหม อาจจะไม่.

ไม่มีทางที่จะรู้ว่ามันคือ Mike จริง ๆ หรือหมายเลขบัญชีที่ถูกต้อง สำหรับทุกสิ่งที่คุณรู้มันอาจเป็นนักต้มตุ๋นที่พยายามจะขโมยจากคุณ แทนที่จะโอนเงินทันทีจะเป็นการดีที่สุดที่จะรอจนกว่าคุณจะเห็นไมค์เพื่อให้คุณสามารถให้เงินสดแก่เขาได้.

เช่นเดียวกับในสถานการณ์ข้างต้นเรามักพบกับสถานการณ์ที่เราต้องการ ตรวจสอบตัวตนของฝ่ายหรือความสมบูรณ์ของข้อมูลในโลกออนไลน์. นั่นเป็นสาเหตุที่ลายเซ็นดิจิทัลเพิ่มขึ้นเป็นกลไกที่สามารถให้คุณสมบัติเหล่านี้และอำนวยความสะดวกในการทำธุรกรรมออนไลน์ที่ปลอดภัย.

หากไม่มีพวกเขาเราอาจไม่ทราบว่าเรากำลังพูดคุยกับใครไม่แน่ใจว่าข้อมูลถูกเปลี่ยนแปลงหรือไม่และบุคคลนั้นสามารถปฏิเสธได้ว่าพวกเขามีความรับผิดชอบ.

การใช้ลายเซ็นดิจิทัล

คุณสมบัติของลายเซ็นดิจิทัลเหล่านี้ทำให้มีประโยชน์ในแอพพลิเคชั่นที่หลากหลาย พวกเขามักจะใช้ด้วยตนเองหรือร่วมกับการเข้ารหัสในช่วงของโปรโตคอลความปลอดภัยที่แตกต่างกันเช่น:

• IPsec
• SSH
• TLS

พวกเขายังใช้บ่อยใน การจัดการสิทธิ์ดิจิทัล, ใน เทคโนโลยี blockchain, ใน การจัดการสัญญา แอปพลิเคชันซึ่งเป็นส่วนหนึ่งของ การกระจายซอฟต์แวร์, และใน การเงิน.

ประวัติลายเซ็นดิจิทัล

ความคิดเกี่ยวกับลายเซ็นดิจิตอลถูกลอยครั้งแรกโดยผู้เข้ารหัสที่มีชื่อเสียง Whitfield Diffie และ Martin Hellman ในบทความของพวกเขา 1976 ทิศทางใหม่ในการเข้ารหัส. ในปี 1978 Ronald Rivest, Adi Shamir และ Len Adleman นำอัลกอริธึม RSA มาสู่มุมมองสาธารณะซึ่งสามารถนำมาใช้ในการสร้างลายเซ็นดิจิทัลที่ไม่ปลอดภัย.

ต้องใช้เวลาอีกสิบกว่าปีกว่าที่ลายเซ็นดิจิทัลจะปรากฏในแอปพลิเคชันที่แพร่หลาย: การเปิดตัว Lotus Notes 1.0 ของ IBM จากนั้นเป็นต้นมาลายเซ็นดิจิทัลเริ่มเห็นการยอมรับที่กว้างขึ้นเมื่อมีเทคนิคใหม่ ๆ เกิดขึ้นและความต้องการการรับรองความถูกต้องออนไลน์และการตรวจสอบความสมบูรณ์ก็เพิ่มขึ้น.

คำแนะนำเบื้องต้นเกี่ยวกับการเข้ารหัสรหัสสาธารณะ

ก่อนที่เราจะกระโดดสู่ลายเซ็นดิจิทัลเราควรจะครอบคลุมบางส่วนที่สำคัญของการเข้ารหัสรหัสสาธารณะ, รูปแบบพื้นฐานของการทำงานของลายเซ็นดิจิทัล.

หากคุณค่อนข้างใหม่ต่อการเข้ารหัสระบบที่คุณคุ้นเคยที่สุดคือการเข้ารหัสแบบสมมาตร – คีย์ นี่หมายถึงว่าคีย์เดียวกัน (ซึ่งคล้ายกับรหัสผ่าน แต่มีความแตกต่างบางอย่าง) ใช้ในการเข้ารหัสและถอดรหัสข้อมูล.

การเข้ารหัสคีย์สาธารณะเป็นการปฏิวัติเพราะเกี่ยวข้อง ใช้ปุ่มแยกต่างหากสำหรับกระบวนการเข้ารหัสและถอดรหัส, นำไปสู่แอพพลิเคชั่นเข้ารหัสลับที่หลากหลาย คีย์สองตัวนี้สร้างคู่ของคีย์ประกอบด้วยคีย์สาธารณะและคีย์ส่วนตัว รหัสสาธารณะสามารถแชร์กับสาธารณะได้อย่างชัดเจนในขณะที่รหัสส่วนตัวจะต้องถูกเก็บเป็นความลับเพื่อให้ระบบมีความปลอดภัย.

การใช้คีย์สาธารณะสองแบบที่พบบ่อยที่สุดคือการเข้ารหัสและลายเซ็นดิจิทัล.

การเข้ารหัสลับ

หนึ่งในคุณสมบัติที่ก้าวล้ำของการเข้ารหัสคีย์สาธารณะคือ อนุญาตให้ฝ่ายที่ไม่เคยพบเจอส่งข้อความถึงกันอย่างเป็นความลับ. ผู้ส่งค้นหาคีย์สาธารณะของผู้รับที่ต้องการ (สามารถพบได้ในเซิร์ฟเวอร์กุญแจสาธารณะบนเว็บไซต์ส่วนตัวหรือเพียงแค่ถามบุคคล) จากนั้นเข้ารหัสข้อความด้วยคีย์นี้ก่อนที่จะส่งไปยังผู้รับ.

ผู้รับเป็นบุคคลเพียงคนเดียวที่สามารถเข้าถึงข้อความได้ – สมมติว่ารหัสส่วนตัวไม่ได้ถูกบุกรุก – โดยการถอดรหัสด้วยกุญแจส่วนตัวของพวกเขา แม้ว่าจะใช้รหัสสาธารณะเพื่อเข้ารหัสข้อความ แต่ก็สามารถถอดรหัสได้ด้วยรหัสส่วนตัวเท่านั้น หากผู้รับต้องการที่จะตอบพวกเขาพบกุญแจสาธารณะของผู้ส่งเดิมจากนั้นทำซ้ำกระบวนการ.

ดูเพิ่มเติมที่: อธิบายประเภทการเข้ารหัสทั่วไป

ลายเซ็นดิจิทัลทำงานอย่างไร?

อย่างที่เราได้กล่าวไปแล้วลายเซ็นดิจิตอลนั้นใช้สำหรับการตรวจสอบเพื่อดูว่าข้อมูลได้รับการแก้ไขหรือไม่ มีกลไกที่แตกต่างหลากหลายที่สามารถใช้สำหรับลายเซ็นดิจิทัลและพวกเขาแต่ละคนมีการเปลี่ยนแปลงเล็กน้อยในวิธีการที่พวกเขามีโครงสร้าง.

โดยทั่วไปอัลกอริทึมเหล่านี้จะต้องประกอบด้วยอัลกอริธึมย่อยสามประการ:

• อัลกอริธึมการสร้างคีย์ – อัลกอริทึมนี้สร้างคู่ของคีย์แบบสุ่มสำหรับผู้ใช้ ตัวเลขที่เกี่ยวข้องในคู่คีย์จำเป็นต้องปฏิบัติตามพารามิเตอร์บางอย่างเพื่อให้ปลอดภัย สองสิ่งที่สำคัญที่สุดคือตัวเลขมีขนาดแบบสุ่มและขนาดที่เพียงพอ.
• อัลกอริทึมสำหรับการลงนามข้อมูล – เมื่อผู้ใช้มีกุญแจของพวกเขามีวิธีเฉพาะสำหรับวิธีที่พวกเขาใช้กับข้อมูลในกระบวนการลายเซ็น.
• อัลกอริทึมสำหรับตรวจสอบลายเซ็น – เช่นเดียวกันการยืนยันลายเซ็นต์จะเป็นไปตามกระบวนการที่กำหนดไว้ล่วงหน้า.

เพื่อให้ระบบลายเซ็นดิจิทัลมีประสิทธิภาพจะต้องมีโครงสร้างในลักษณะที่:

• ข้อมูลที่เซ็นชื่อด้วยรหัสส่วนตัวคือ ยืนยันด้วยรหัสสาธารณะที่ตรงกันของบุคคลเดียวกัน.
• มันเป็นไปไม่ได้โดยพื้นฐานแล้ว (ใช้เทคโนโลยีและเทคนิคในปัจจุบัน) ในการปลอมแปลงลายเซ็นที่ถูกต้องโดยไม่ทราบว่ากุญแจส่วนตัวของแต่ละคน.

ชุดลายเซ็นดิจิตัลที่พบบ่อยที่สุด ได้แก่ RSA, DSA, EcDSA และ EdDSA.

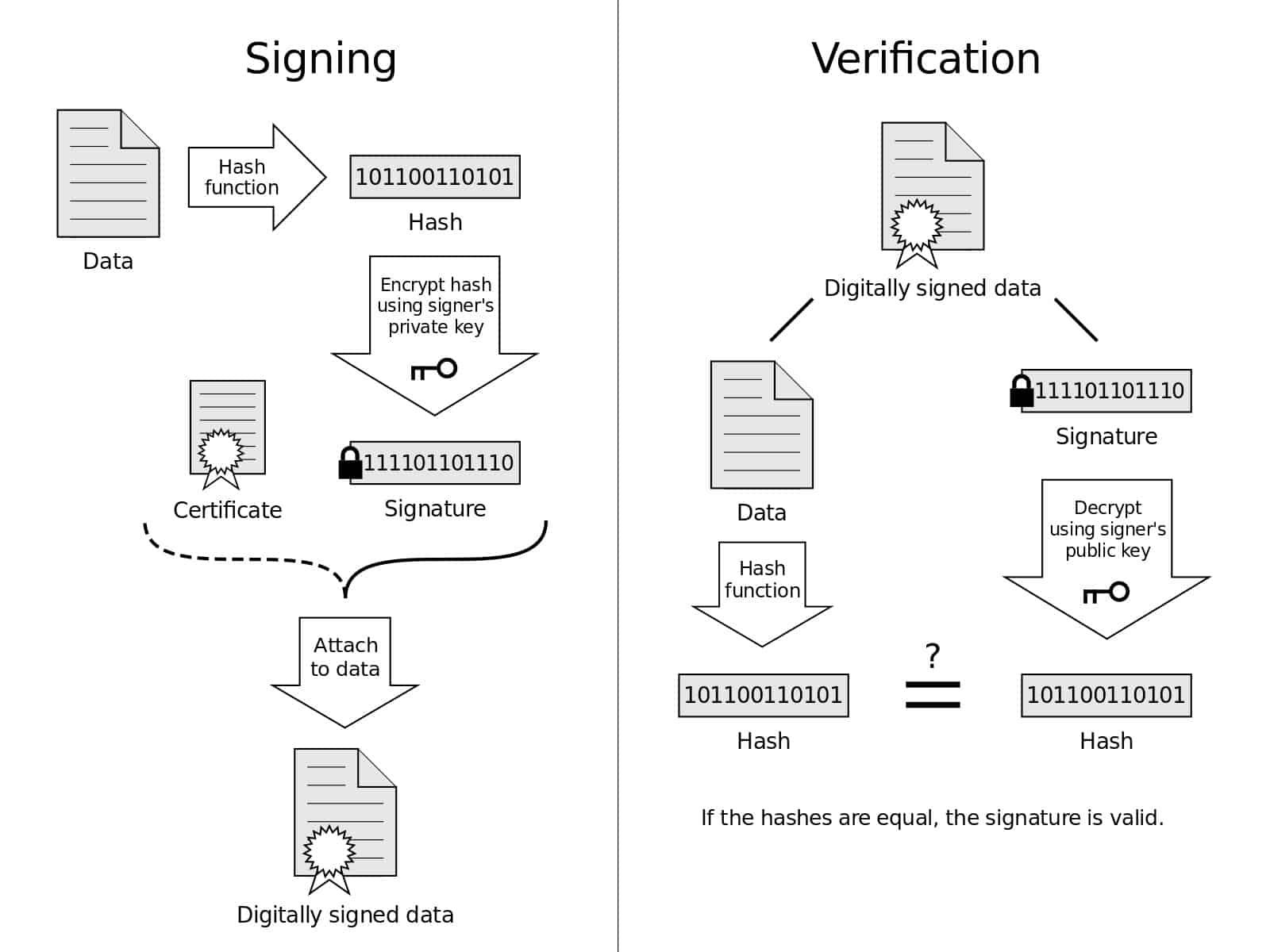
รูปภาพนี้ให้ภาพที่เป็นตัวแทนของกระบวนการเซ็นชื่อและการตรวจสอบ. แผนภาพลายเซ็นดิจิทัล โดย Acdx อนุญาตภายใต้ มอนส์ CC0

อาร์เอส

RSA เป็นอัลกอริธึมลายเซ็นดิจิตอลแรก แต่ก็สามารถใช้สำหรับการเข้ารหัสคีย์สาธารณะ ในบทความนี้เราจะข้ามไปด้านการเข้ารหัส แต่คุณสามารถหาข้อมูลเพิ่มเติมเกี่ยวกับมันในบทความที่ครอบคลุมของเราที่ครอบคลุม RSA คืออะไรและวิธีการทำงาน.

การสร้างคีย์ RSA

ในการใช้งานที่ปลอดภัยของ RSA โดยทั่วไปคู่คีย์จะถูกสร้างขึ้นโดยอัตโนมัติภายใต้กระบวนการต่อไปนี้:

รุ่นพิเศษ

เลือกหมายเลขเฉพาะบุคคลสองตัว, พี และ Q. ขนาดที่แน่นอนของจำนวนเฉพาะเหล่านี้จะแตกต่างกันไปขึ้นอยู่กับขนาดของคีย์ วันนี้เราแนะนำให้ใช้คีย์ RSA อย่างน้อย 2048 บิตเพื่อความปลอดภัยที่เพียงพอดังนั้นเราจึงพูดถึงตัวเลขสำคัญสองตัวที่คูณเพื่อสร้างหมายเลข 2048 บิต.

2048 บิตเป็นขนาดในระบบเลขฐานสอง หากจำนวนขนาดนี้ถูกแปลงเป็นระบบทศนิยมที่เราคุ้นเคยมากกว่ามันจะยาวประมาณ:

790279459827301874397592846209502937592870495029380589710393

7019019209839375970193850891039510730584153687576287365984259

3824756984376582763487912837582736592873684273684728938575872

4958729873958729835792875982795837529876348273685729843579348

7958458720948602984912837502948019371092482793857928739548772

3975928375924785938670358103799581093750193850791345986792384

7378267352673547623568734869386945673456827659493849024875809

6039429837592834759348759384759284780634701938091803984091804

9810938592873995710901985013984019835091835019830910791803958

1039519039518093581093850198401935801938401983409180938510983

09180019

จำนวนเฉพาะใน RSA จะต้องเลือกแบบสุ่มและควรมีความยาวใกล้เคียงกัน.

ในตัวอย่างของเราเราจะใช้ตัวเลขที่น้อยกว่ามากเพื่อทำให้เข้าใจง่ายขึ้น โปรดทราบว่าการใช้แป้นขนาดนี้จะทำให้ลายเซ็นดิจิทัลเป็นของปลอม นี่คือเหตุผลที่ใช้ค่าขนาดใหญ่ดังกล่าวในทางปฏิบัติ.

สมมติว่า:

พี = 13

Q = 17

ขั้นตอนแรกคือการคำนวณค่าโมดูลัส n ใช้สูตรต่อไปนี้:

n = pq

n = 13 x 17

n = 221

คุณค่าของ n ยังเป็นความยาวกุญแจ.

ฟังก์ชั่น Totient ของ Carmichael

ตอนนี้เรามีค่าสำหรับ n, ขั้นตอนต่อไปคือการใช้ฟังก์ชั่น Totient ของ Carmichael:

λ(n) = LCM (พี – 1, Q – 1)

มีบางสิ่งที่คุณต้องเข้าใจ:

• λ(n) หมายถึงผลรวมของ Carmichael สำหรับค่าของ n
• LCM แสดงถึงตัวคูณสามัญต่ำสุด นี่คือหมายเลขทั่วไปที่ต่ำที่สุดที่ทั้งคู่ P-1 และ Q-1 สามารถแบ่งออกเป็น

มาเสียบตัวเลขของเราเข้ากับสมการ:

λ(221) = LCM (13 – 1, 17 – 1)

λ(221) = LCM (12, 16)

หากคุณเก่งคณิตศาสตร์ทางจิตคุณก็อาจจะคิดได้ 48 เป็นตัวคูณร่วมที่ต่ำที่สุดของทั้งสอง 12 และ 16. นี่เป็นเพราะ 48 เป็นจำนวนที่เล็กที่สุดที่ทั้งสองหมายเลขสามารถใส่ได้ (12 x 4 = 48, 16 x 3 = 48) ดังนั้น:

λ(221) = 48

มาพร้อมกับรหัสสาธารณะ

ใน RSA คีย์สาธารณะประกอบด้วยค่า n (ซึ่งเราคำนวณมาแล้วเป็น 221) และ อี. เนื่องจากคีย์สาธารณะถูกแชร์อย่างอิสระค่าสำหรับ อี ไม่จำเป็นต้องเป็นความลับ ในความเป็นจริงมันมักจะถูกตั้งค่าไว้ที่ 65,537 ในทางปฏิบัติเพราะตัวเลขที่มากขึ้นจะทำให้กระบวนการเข้ารหัสช้าลง ในตัวอย่างของเราเราจะตั้งค่า อี ถึง 5, เพียงเพื่อให้มันเป็นจำนวนน้อยและง่ายต่อการทำงานกับ.

ดังนั้นกุญแจสาธารณะสำหรับตัวอย่างนี้ประกอบด้วย 221 และ 5. เราจะครอบคลุมเฉพาะวิธีการใช้รหัสสาธารณะในส่วนต่อไปนี้.

การหาคีย์ส่วนตัว

เช่นเดียวกับกุญแจสาธารณะของเราประกอบด้วยสองตัวเลขดังนั้นกุญแจส่วนตัวของเราก็คือ คีย์ส่วนตัวประกอบด้วย d และ อี. เรารู้คุณค่าแล้ว อี (5), และเราสามารถใช้สูตรต่อไปนี้เพื่อค้นหา d:

d = 1 /อี พอควร λ(n)

สังเกตได้ว่า พอควร เพียงแค่สัญลักษณ์การดำเนินการโมดูโลซึ่งโดยปกติจะหมายความว่าคุณต้องค้นหาส่วนที่เหลือเมื่อคุณแบ่งด้านซ้ายทางขวา ตัวอย่างเช่น:

17 mod 3 = 2

นี่เป็นเพราะ 3 พอดีกับ 17 รวม 5 ครั้งส่วนที่เหลือ 2.

ตัวอย่างของเรานั้นแตกต่างกันเล็กน้อย “1 /อี พอควร” ส่วนของสมการอาจบอกให้คุณแบ่ง 1 โดย อี, แต่จริงๆแล้วมันไม่ได้เป็น มันสับสน แต่นี่เป็นวิธีการแทน โมดูลผกผัน. สมการนี้บอกให้เราคำนวณค่าผกผันแบบแยกส่วนของ อี และ λ(n).

โดยทั่วไปการผกผันโมดูลาร์ได้มาจากการใช้อัลกอริทึมแบบยุคลิดแบบขยาย แต่เราจะไม่ครอบคลุมในบทความนี้ แต่เราเพียงแค่ใช้เครื่องคิดเลขออนไลน์เพื่อทำให้สิ่งต่าง ๆ ง่ายขึ้น.

ตอนนี้เราได้รับสิ่งนั้นแล้วให้ป้อนค่าของเราลงในสูตร:

d = 1/5 mod 48

การค้นหา d, สิ่งที่เราต้องทำคือป้อนค่าของเราสำหรับ อี (5) เป็นเครื่องคิดเลขออนไลน์ที่มันบอกว่า จำนวนเต็ม, แล้วคุณค่าของเราสำหรับ λ(n), ซึ่งเป็น 48, ที่มันบอกว่า โมดูโล.

สิ่งนี้ทำให้เราได้ผลลัพธ์จาก 29 ตามเครื่องคิดเลขออนไลน์ ดังนั้นรหัสส่วนตัวของเราจะประกอบด้วย:

อี = 5

d = 29.

ตอนนี้เราได้สร้างกุญแจทั้งสองของเราแล้วคำถามต่อไปคือ “เราจะทำอย่างไรกับพวกเขา” เราสามารถใช้พวกเขาในการเข้ารหัสและถอดรหัสข้อความผ่านการเข้ารหัสคีย์สาธารณะ แต่บทความนี้เกี่ยวกับลายเซ็นดิจิตอลดังนั้น เราจะมุ่งเน้นที่.

การเซ็นชื่อแบบดิจิทัลด้วย RSA

สมมติว่ามีคนต้องการส่งข้อความถึงเพื่อน แต่พวกเขาต้องการตรวจสอบให้แน่ใจว่าเพื่อนสามารถยืนยันความถูกต้องและความสมบูรณ์ของข้อความได้ พวกเขาสามารถทำได้โดยใช้ลายเซ็นดิจิทัล RSA เพื่อเซ็นข้อความ.

ขั้นตอนแรกคือการ เรียกใช้ข้อความทั้งหมดผ่านฟังก์ชั่นแฮช. เหล่านี้เป็นฟังก์ชั่นทางเดียวซึ่งจะส่งสัญญาณเอาต์พุตเดียวกันสำหรับอินพุตที่กำหนด ฟังก์ชั่นแฮชที่ปลอดภัยนั้นเป็นไปไม่ได้ที่จะกลับด้านซึ่งหมายความว่าไม่สามารถใช้เอาต์พุตเพื่อหาอินพุตได้ นอกจากนี้ยังเป็นไปไม่ได้ที่ข้อความสองข้อความที่แยกกันจะมีเอาต์พุตเดียวกัน.

คุณสามารถค้นหาข้อมูลเพิ่มเติมเกี่ยวกับฟังก์ชันแฮชได้ใน สิ่งที่คร่ำครวญ? ส่วนของบทความของเรา, การเข้ารหัส, การแปลงแป้นพิมพ์, การเติมเกลือ – สิ่งที่แตกต่าง?

สมมติว่าเราต้องการเซ็นข้อความแบบดิจิทัล“วันนี้ร้อน” เพื่อให้ผู้รับของเราสามารถรู้ได้ว่าข้อความนั้นเป็นของจริงหรือไม่และหากได้รับการดัดแปลง ดังนั้นเราจะเรียกใช้“วันนี้ร้อน” ผ่านฟังก์ชั่นแฮช.

ทำความเข้าใจเกี่ยวกับฟังก์ชั่นแฮช

วันนี้ฟังก์ชั่นแฮชที่ใช้บ่อยที่สุดคือ SHA-256 เมื่อเราส่งข้อความของเราผ่านเครื่องคิดเลข SHA-256 ออนไลน์มันจะให้ผลลัพธ์ดังนี้:

efbcf22b4cd04d49daa87cfbda7d2313cc665c35bc9e18954af16c104a731952

นี่ทำให้เกิดปัญหาเล็กน้อยสำหรับตัวอย่างของเรา ข้อแรกคือมันไม่ใช่เลขทศนิยมเหมือนที่คนส่วนใหญ่คุ้นเคย คุณอาจสังเกตเห็นว่ามีตัวอักษรในหมายเลขนี้และพวกเขาเท่านั้นไปถึง ฉ. นี่ทำให้เรารู้ว่ามันเป็นเลขฐานสิบหก.

ระบบเลขฐานสิบหกอาศัยฐาน 16 แทนฐาน 10, เช่นระบบตัวเลขที่ปกติเราใช้ ซึ่งหมายความว่าแทนที่จะนับเป็นทวีคูณของ 10 จะนับเป็นทวีคูณของ 16 และตัวอักษร 6 ตัวแรกของเราถูกนำมาใช้เพื่อสร้างตัวเลขพิเศษเหล่านี้ จำนวนนี้สามารถแปลงเป็นระบบทศนิยมของเราทุกวัน แต่ไม่เกินขอบเขตของบทความนี้.

ประเด็นที่สองที่เรามีคือมันเป็นจำนวนมากจริงๆ ถ้ามันถูกแปลงเป็นทศนิยมมันจะยิ่งนานขึ้น เนื่องจากเรามีเป้าหมายเพื่อความเรียบง่ายในคู่มือนี้การใช้การคำนวณด้วยจำนวนที่มากเช่นนี้จะทำให้สิ่งต่าง ๆ สับสนเกินกว่าที่จะรับแนวคิดพื้นฐานทั่ว.

ด้วยแนวคิดในการแสดงให้เห็นว่าลายเซ็นดิจิทัล RSA ทำงานอย่างไรในลักษณะที่เข้าใจง่ายเราจะไม่ใช้ค่าแฮชขนาดใหญ่ในตัวอย่างต่อไปนี้ แต่เราจะทำเป็นว่าค่าแฮชของ“ แทน”วันนี้ร้อน” เป็นเพียงแค่ 10.

เราจะต้องแสร้งว่าเช่นเดียวกับแฮชจริงทุกครั้งที่เราใส่ข้อมูล“ มันร้อนวันนี้” ผ่านฟังก์ชั่นแฮชมันจะคืนค่าของ 10. เพื่อให้สอดคล้องกับวิธีการทำงานของแฮชตามปกติเราจะต้องแกล้งทำเป็นว่าไม่น่าเป็นไปได้ที่อินพุตอื่นจะให้ค่าเดียวกัน ในทำนองเดียวกันเราต้องแสร้งว่ามันเป็นไปไม่ได้ที่จะเข้าใจว่าข้อมูลต้นฉบับของเราจากค่านี้ คุณสมบัติเหล่านี้คือสิ่งที่ทำให้แฮชมีประโยชน์อย่างมาก.

วิธีใช้ไพรเวตคีย์ของผู้ส่งเพื่อเซ็นค่าแฮชแบบดิจิทัล

ผู้ส่งของเราพิมพ์ข้อความของพวกเขาแล้วใส่มันผ่านฟังก์ชั่นแฮชซึ่งเราทำท่าจะคืนค่าเป็น 10. เมื่อผู้ส่งมีแฮชของข้อความพวกเขาสามารถสร้างลายเซ็นดิจิทัลโดยใช้ไพรเวตคีย์ของพวกเขากับค่าแฮชด้วยสูตรต่อไปนี้:

ม. (ค) = คd พอควร n

นี่เป็นสูตรสำหรับถอดรหัสข้อมูลที่เข้ารหัสด้วยรหัสสาธารณะของผู้รับ แต่ก็ใช้สำหรับการเซ็นเอกสารแบบดิจิทัล.

เมื่อพูดถึงลายเซ็นดิจิทัล:

• คุณค่าของ ม. (ค) จะเป็นลายเซ็นต์.
• คุณค่าของ ค เป็นแฮชของข้อความ (10).
• คุณค่าของ d เป็นส่วนหนึ่งของรหัสส่วนตัวของผู้ส่งซึ่งเราได้รับมาก่อนหน้านี้ (29).
• พอควร function เป็นการดำเนินการที่เหลือเหมือนกับที่เรากล่าวถึงก่อนหน้านี้.
• คุณค่าของ n เป็นอีกส่วนหนึ่งของรหัสส่วนตัวของผู้ส่งซึ่งเราคำนวณเมื่อเริ่มต้น (221).

ดังนั้นเอามาเป็นสูตรของเรา:

ม. (ค) = 1029 mod 221

    ม. (ค) = 100,000,000,000,000,000,000,000,000,000 mod 221

มาทำงานด้วยเครื่องคิดเลขโมดูโลต่อไปนี้ (เราอธิบายว่าการทำงานเหล่านี้ทำงานภายใต้ การหากุญแจสาธารณะ มาตรา). เพื่อให้ทำงานได้อย่างถูกต้องเราต้องตั้งค่าอินพุตของเราเป็น:

• จำนวน ประเภท – ทศนิยม
• จำนวน ค่า – 100000000000000000000000000000
• จำนวน ข ประเภท – ทศนิยม
• จำนวน ข ค่า – 221
• การคำนวณสมการ mod (A, B)

หากคุณทำสิ่งต่างๆอย่างถูกต้องควรมีลักษณะดังนี้:

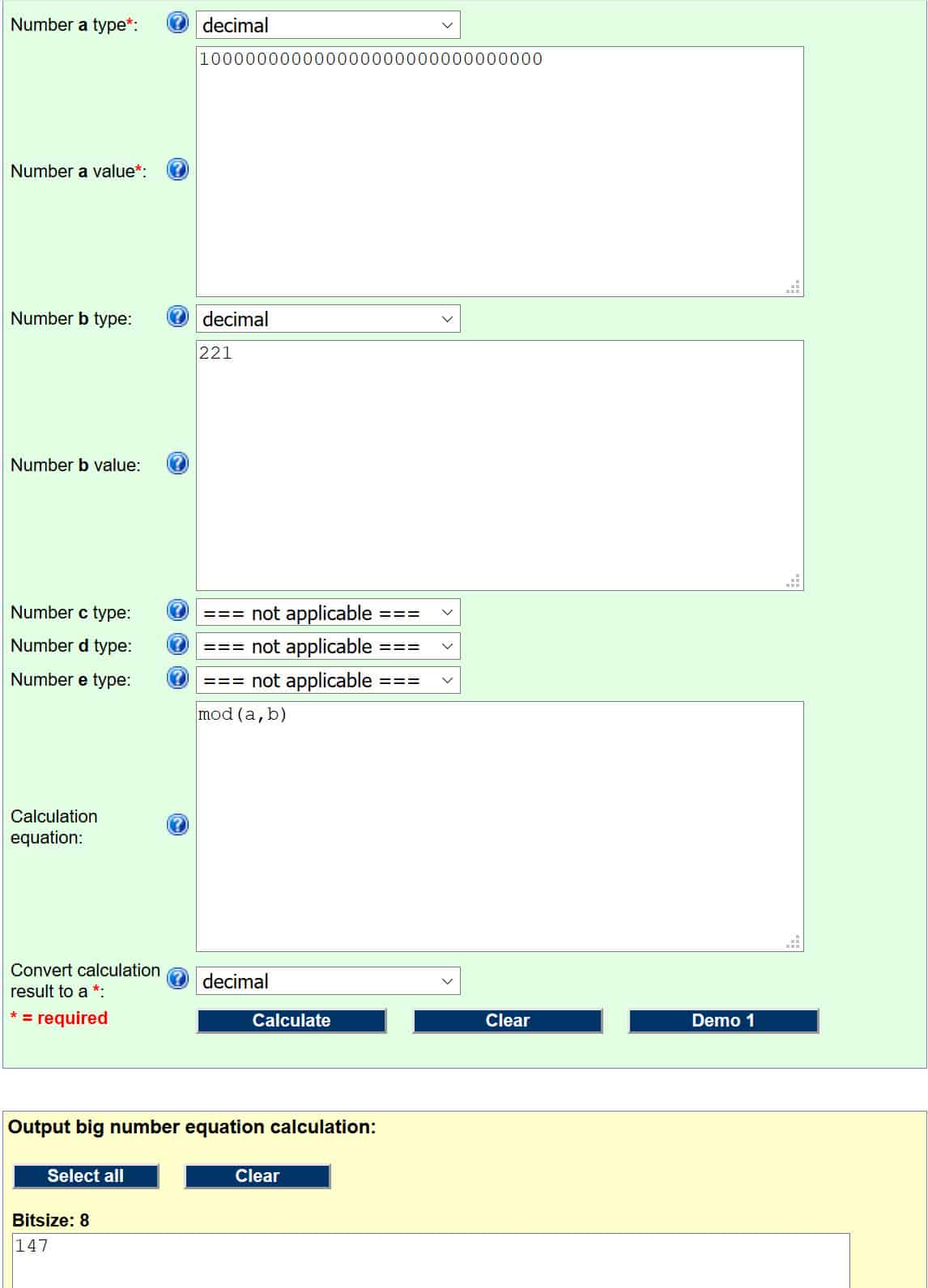
หมายเลขในกล่องสีเหลืองคือคำตอบของเราดังนั้นลายเซ็นดิจิทัลสำหรับการแฮชของข้อความคือ 147.

เพื่อพิสูจน์ความถูกต้องและความสมบูรณ์ของข้อความรวมถึงการไม่ปฏิเสธผู้ส่งของเราจะส่งข้อความ“วันนี้ร้อน” ควบคู่ไปกับลายเซ็นดิจิตอลของ 147 ถึงผู้รับที่ต้องการ เพียงจำไว้ว่าเราใช้ค่าเล็กน้อยสำหรับแฮชเพื่อทำให้สิ่งต่าง ๆ ง่ายขึ้นแทนที่จะเป็นแฮชจริงของข้อความ.

การตรวจสอบลายเซ็นดิจิทัล

ลายเซ็นดิจิทัลมีประโยชน์ก็ต่อเมื่อเราสามารถตรวจสอบได้ว่าถูกต้องหรือไม่ ตราบใดที่คีย์ส่วนตัวของผู้ส่งยังไม่ได้รับอันตรายผู้รับสามารถทดสอบว่าข้อความนั้นเป็นของแท้หรือไม่

    C (เมตร) = ม.อี พอควร n

ในการกลับรายการของกระบวนการเซ็นชื่อนี่เป็นสูตรที่ใช้ในการเข้ารหัสข้อมูลใน RSA เมื่อเราใช้สูตรนี้เพื่อตรวจสอบลายเซ็น:

• คุณค่าของ ค (m) จะเป็นค่าแฮชของผู้ส่งในเวลาที่พวกเขาลงนาม (เนื่องจากโครงสร้างของอัลกอริทึมคีย์สาธารณะของ RSA การใช้กุญแจสาธารณะของผู้ส่งผ่านสูตรนี้จะยกเลิกการดำเนินการลงนามที่เราเพิ่งดำเนินการ ).
• คุณค่าของ ม. คือลายเซ็นดิจิตอล (147).
• คุณค่าของ อี เป็นส่วนหนึ่งของรหัสสาธารณะของผู้ส่งซึ่งเราได้รับมาก่อนหน้านี้ (5).
• พอควร function เป็นการดำเนินการที่เหลือเหมือนกับที่เรากล่าวถึงก่อนหน้านี้.
• คุณค่าของ n เป็นอีกส่วนหนึ่งของรหัสสาธารณะของผู้ส่งซึ่งเราคำนวณเมื่อเริ่มต้น (221).

มาโยนลงในสูตรทั้งหมด:

    C (เมตร) = 1475 mod 221

    C (เมตร) = 68,641,485,507 mod 221

ให้ใช้เครื่องคิดเลขแบบโมดูโลเหมือนเดิมและเก็บทุกอย่างไว้เหมือนกันยกเว้น:

• จำนวน ค่า – 68641485507

หากคุณป้อนข้อมูลถูกต้องคุณควรได้รับผลลัพธ์ดังนี้:

C (เมตร) = 10

ตอนนี้ผู้รับได้คำนวณค่าแฮชจากลายเซ็นดิจิทัลขั้นตอนต่อไปคือการคำนวณค่าแฮชของข้อความที่พวกเขาได้รับ“วันนี้ร้อน” หากคุณจำจากก่อนหน้านี้เราไม่ได้ใช้แฮช SHA-256 จริงของข้อความเพราะจำนวนจะใหญ่เกินไปและทำให้ตัวอย่างซับซ้อนเกินไป.

แต่เราแสร้งว่าฟังก์ชันแฮชทำให้เรามีจำนวนน้อย, 10, สำหรับการป้อนข้อมูลของเรา เนื่องจากฟังก์ชันแฮชจะให้ผลลัพธ์เหมือนกันเสมอสำหรับอินพุตที่กำหนดเมื่อผู้รับของเราใส่“วันนี้ร้อน” ผ่านฟังก์ชั่นแฮชจำนวนจินตภาพของพวกเขาพวกเขาก็จะได้รับคุณค่าของ 10.

กระบวนการตรวจสอบลายเซ็นส่งผลให้มีสองค่า ค่าแรกคือแฮชเหมือนเดิมเมื่อผู้ส่งเซ็นชื่อแบบดิจิทัลด้วยรหัสส่วนตัวของพวกเขา เราคำนวณสิ่งนี้ด้านบนโดยใช้รหัสสาธารณะของผู้ส่ง.

ค่าที่สองคือแฮชของข้อความที่ผู้รับได้รับ คำนวณโดยใช้ฟังก์ชันแฮชเดียวกันกับที่ผู้ส่งเคยใช้แฮชข้อความดั้งเดิม จากนั้นจะเปรียบเทียบค่าทั้งสองนี้และหากค่าเหมือนกันเราสามารถสันนิษฐานได้ว่าข้อความดังกล่าวเป็นของแท้รักษาความสมบูรณ์ของข้อความและไม่สามารถปฏิเสธได้ แน่นอนนี่ถือว่ากุญแจส่วนตัวของผู้ส่งไม่ได้ถูกบุกรุก.

เนื่องจากตัวอย่างของเราคืนค่าเป็น 10 สำหรับแฮชเมื่อมีการลงชื่อโดยผู้ส่งรวมถึงค่า 10 เมื่อแฮชของข้อความที่ได้รับเราสามารถสรุปได้ว่าข้อความ“วันนี้ร้อน” มาจากบุคคลที่อ้างว่าส่งมาและไม่ได้ทำการเปลี่ยนแปลงนับตั้งแต่ถูกส่งมา.

หากผู้รับต้องการตอบสนองเพื่อให้ผู้สื่อข่าวสามารถตรวจสอบข้อความของพวกเขาในลักษณะเดียวกันกระบวนการทั้งหมดจะถูกทำซ้ำยกเว้นกุญแจส่วนตัวและกุญแจสาธารณะของผู้รับจะถูกใช้สำหรับกระบวนการเซ็นชื่อและการตรวจสอบตามลำดับ.

คณิตศาสตร์ทั้งหมดนี้อาจทำให้คุณหมดความคิดในเรื่องของลายเซ็นดิจิทัล ไม่ต้องกังวลเพราะการติดตั้ง RSA จะทำให้กระบวนการนี้เป็นไปโดยอัตโนมัติดังนั้นคุณจึงไม่จำเป็นต้องกระทืบตัวเลขใด ๆ.

ข้อดี RSA & ข้อเสีย

RSA เป็นหนึ่งในอัลกอริธึมลายเซ็นดิจิตอลที่ได้รับการสนับสนุนอย่างกว้างขวางที่สุดแม้ว่าจะมีการพัฒนาไปสู่อัลกอริธึมใหม่ที่มีประสิทธิภาพและปลอดภัยยิ่งขึ้นเช่น ECDSA และ EdDSA.

เมื่อเปรียบเทียบกับ DSA (ซึ่งเราจะกล่าวถึงในส่วนถัดไป) RSA นั้นเร็วกว่าในการตรวจสอบลายเซ็น แต่ช้ากว่าในการสร้างพวกเขา เนื่องจากลายเซ็นมีแนวโน้มที่จะสร้างครั้งเดียวและตรวจสอบหลายครั้ง RSA จึงเป็นที่ต้องการมากกว่า DSA.

DSA

ความปลอดภัยของอัลกอริธึมลายเซ็นดิจิตอลขึ้นอยู่กับแนวคิดทางคณิตศาสตร์สองประการปัญหาลอการิทึมแบบไม่ต่อเนื่องและคุณสมบัติบางอย่างของการยกกำลังแบบแยกส่วน สำหรับบางกลุ่มมันเป็นไปไม่ได้ที่จะคำนวณลอการิทึมแบบไม่ต่อเนื่องของพวกเขาด้วยเทคนิคและเทคโนโลยีในปัจจุบัน.

การสร้างคีย์ DSA

ในการสร้างคีย์ DSA ขั้นตอนแรกคือการเลือกพารามิเตอร์ที่กลุ่มผู้ใช้ในระบบเดียวกันสามารถใช้เพื่อสร้างคู่คีย์.

การสร้างพารามิเตอร์

• การเลือก ฟังก์ชันแฮช – SHA-256 เป็นตัวเลือกที่พบบ่อยที่สุดเพื่อตอบสนองความต้องการด้านความปลอดภัยที่ทันสมัย.
• การตกลงกับความยาวของคีย์, L และ ยังไม่มีข้อความ – วันนี้, L ควรมีความยาวอย่างน้อย 2,048 บิตในขณะที่ ยังไม่มีข้อความ ควรมีอย่างน้อย 256 บิต.
• ตัดสินใจเลือกนายก, Q, นั่นคือความยาวเท่ากัน ยังไม่มีข้อความ.
• เลือกเฉพาะ, พี, ที่ไหน พี-1 คือตัวคูณของ Q.
• เลือกตัวเลข, ก., ใช้สูตรต่อไปนี้ (ที่ไหน ชั่วโมง เป็นจำนวนที่กำหนดเองระหว่าง 1 ถึง P-1):

ก. = ชั่วโมง(พี – 1) /Q พอควร พี

โดยทั่วไปค่าเหล่านี้เป็นตัวเลขที่มีขนาดใหญ่มากเพื่อให้อัลกอริทึมมีความปลอดภัย เพื่อให้ตัวอย่างของเราไม่สามารถคำนวณหรืออธิบายได้ยากเกินไปเราจะใช้ตัวเลขจำนวนน้อยมากที่ไม่ปลอดภัย สมมติว่า:

    Q = 5

    พี = 11

การค้นหา ก., เราเสียบตัวเลขของเราลงในสูตร เราจะใช้ 3 เป็นค่าของเราสำหรับ ชั่วโมง:

ก. = 3 (11-1) / 5 mod 11

ก. = 32 mod 11

ก. = 9 mod 11

เราจะใช้เครื่องคิดเลขแบบโมดูโลเหมือนกับใน วิธีใช้ไพรเวตคีย์ของผู้ส่งเพื่อเซ็นค่าแฮชแบบดิจิทัล มาตรา. พารามิเตอร์จะเหมือนกันยกเว้น:

• จำนวน ค่า – 9
• จำนวน ข ค่า – 11

หากคุณป้อนทุกอย่างถูกต้องแล้วมันจะให้ผลลัพธ์แก่คุณ ก. ของ 9.

สร้างรหัสผู้ใช้

จากนั้นผู้ใช้แต่ละคนจะใช้พารามิเตอร์เหล่านี้และใช้พวกเขาในการสร้างคู่คีย์ของพวกเขา:

• กุญแจส่วนตัว (x) เป็นตัวเลขที่อยู่ระหว่าง 0 และ Q, ซึ่งเราตั้งไว้ที่ 5 สำหรับตัวอย่างของเราเราจะเลือก 2 เป็น x, กุญแจส่วนตัวของเรา.
• กุญแจสาธารณะ (Y) คำนวณโดยใช้สูตรต่อไปนี้:

    Y = ก.x พอควร พี

ดังนั้น:

Y = 92 mod 11

Y = 81 mod 11

เราจะใช้เครื่องคิดเลขแบบโมดูโลเดียวกันอีกครั้ง พารามิเตอร์จะเหมือนกันยกเว้น:

• จำนวน ค่า – 81
• จำนวน ข ค่า – 11

หากคุณป้อนข้อมูลถูกต้องคุณควรได้รับผลลัพธ์ y = 4. ดังนั้นกุญแจสาธารณะจึงเป็น 4.

ตอนนี้เราได้สร้างคุณค่าทั้งหมดของเรามาแล้วให้คุณสรุปอย่างรวดเร็ว พารามิเตอร์สำหรับระบบคือ:

• พี = 11
• Q = 5
• ก. = 9

คู่กุญแจของเราประกอบด้วย:

• คีย์ส่วนตัว, x = 2
• กุญแจสาธารณะ, Y = 4

การเซ็นชื่อแบบดิจิทัลด้วย DSA

ผู้ส่งสามารถใช้รหัสส่วนตัวของ DSA ในการเซ็นชื่อแบบดิจิทัลซึ่งช่วยให้ผู้รับสามารถตรวจสอบได้ว่าข้อความนั้นเป็นของแท้หรือไม่และยังคงความสมบูรณ์อยู่ นอกจากนี้ยังป้องกันไม่ให้ผู้ส่งสามารถปฏิเสธข้อความได้.

กระบวนการลายเซ็นเริ่มต้นด้วยการสร้างค่าสุ่ม k, ซึ่งอยู่ระหว่าง 1 และ Q. สำหรับตัวอย่างนี้มาเลือกกัน 3 เป็นหมายเลข “สุ่ม” ของเรา, k.

จากนั้นเราปฏิบัติตามสูตรต่อไปนี้เพื่อสร้างรหัสบุคคล (R) สำหรับข้อความ:

R = (ก.k พอควร พี) mod q

มาโยนตัวเลขของเรา:

R = (93 mod 11) mod 5

R = (729 mod 11) mod 5

เราใช้เครื่องคำนวณโมดูโลของเราอีกครั้งเพื่อเข้าสู่ 729 และ 11, ซึ่งทำให้เรามีผลมาจาก 3. ดังนั้น:

R = 3 mod 5

จากนั้นเราก็ทำซ้ำการดำเนินการแบบโมดูโลอีกครั้งด้วยค่าใหม่เพื่อให้เรา:

R = 3

คุณค่าของเราสำหรับ R ถูกใช้เป็นกุญแจสำคัญสำหรับข้อความ.

เราเกิดขึ้นกับส่วนอื่น ๆ ของลายเซ็นดิจิทัล, s, ด้วยสูตรดังต่อไปนี้:

s = k-1(H(ม.) + XR) mod Q

k-1 ไม่ได้แสดงถึงการใช้พลังงานเชิงลบ k, แต่แทนที่จะคำนวณโมดุลผกผันเหมือนกับในของเรา การหาส่วนย่อยของคีย์ส่วนตัว ในส่วนก่อนหน้าของบทความที่เราพูดคุยเกี่ยวกับ RSA.

H(ม.) คือค่าแฮชสำหรับข้อความที่ผู้ส่งกำลังเซ็นชื่อ โดยปกตินี่จะเป็นค่าแฮชแบบยาวที่ได้มาจากข้อความเช่นเดียวกับใน ทำความเข้าใจกับค่าแฮช หมวดย่อยข้างต้นซึ่งเรากล่าวถึงเมื่อเราพูดถึงอัลกอริทึม RSA.

สำหรับตัวอย่างนี้เราจะทำให้สิ่งต่าง ๆ ง่ายขึ้น เช่นเดียวกับในส่วนของ RSA เราจะบอกว่าข้อความของเรา, ม., คือ “วันนี้ร้อน” และแฮชของข้อความ H(ม.) คือ 10.

ดังนั้นให้ป้อนค่าทั้งหมดของเราลงในสูตร:

s = 3-1 (10 + 2 x 3) (mod 5)

s = 3-1 (10 + 6) (mod 5)

s = 3-1 (16) (mod 5)

ตอนนี้เราใช้อินเวอร์สโมดูลของ 3 สำหรับคำสั่งของ 5 (เพราะ 5 คือคุณค่าของเราสำหรับ Q) ใช้เครื่องคิดเลขผกผันโมดูลาร์เดียวกันจากก่อนหน้านี้ เข้าสู่ 3 เป็นจำนวนเต็มและ 5 ในฐานะ modulo ซึ่งจะให้ผลลัพธ์ของคุณ 2. ดังนั้น:

s = 2 (16) (mod 5)

s = 32 (mod 5)

กลับไปที่เครื่องคิดเลขของเราเพื่อการทำงานแบบโมดูโลปกติโดยรักษาพารามิเตอร์เดียวกับที่เราใช้ก่อนหน้านี้ยกเว้น:

• จำนวน ค่า – 32
• จำนวน ข ค่า – 5

หากคุณทำสิ่งนี้ถูกต้องแล้วมันจะให้ค่า s ของ 2. ลายเซ็นดิจิตอลประกอบด้วย R และ s (3 และ 2 ตามลำดับ). ผู้ส่งส่งลายเซ็นดิจิทัลไปยังผู้รับของพวกเขาพร้อมกับข้อความของพวกเขา“วันนี้ร้อน” พวกเขายังจะแบ่งปันค่าของ p, q, ก. และ Y กับผู้รับ.

การตรวจสอบลายเซ็นดิจิทัล

เมื่อผู้รับได้รับลายเซ็นดิจิทัลข้างข้อความพวกเขาสามารถตรวจสอบความถูกต้องและความถูกต้องของข้อความด้วยชุดการคำนวณต่อไปนี้.

ขั้นตอนแรกคือค้นหาแฮชของข้อความที่ได้รับ ผู้รับทำได้โดยการเรียกใช้ข้อความทั้งหมดผ่านฟังก์ชั่นแฮช เพื่อให้ทุกอย่างเรียบง่ายและสอดคล้องกันสมมติว่าแฮชของข้อความ, H(ม.) คือ 10.

ผู้รับยังได้รับการส่งค่าต่อไปนี้ซึ่งพวกเขาใช้ในกระบวนการตรวจสอบ:

• ลายเซ็นดิจิตอล (r, s) – 3, 2
• หน้า – 1
• q – 5
• g – 9
• y – 4

การคำนวณครั้งแรกคือการหา W:

W = s-1 ตัว Q

อีกครั้ง s-1 หมายถึงการใช้อินเวอร์สโมดูลาร์ ลองป้อนค่าของเรา:

W = 2-1 mod 5

เราจะใช้เครื่องคิดเลขผกผันแบบแยกส่วนจากก่อนหน้านี้ เข้าสู่ 2 เป็นจำนวนเต็มและ 5 ในฐานะ modulo ซึ่งจะให้ผลลัพธ์ของคุณ 3 สำหรับ W. ขั้นตอนต่อไปคือการหา ยู1 ที่มีสูตรดังต่อไปนี้:

ยู1 = H(ม.) x W พอควร Q

มาแสดงในค่านิยมของเรา:

ยู1 = 10 x 3 mod 5

ยู1 = 30 mod 5

กลับไปที่เครื่องคิดเลขแบบโมดูโลปกติรักษาพารามิเตอร์เดียวกันกับที่เราใช้ก่อนหน้านี้ยกเว้น:

• จำนวน ค่า – 30
• จำนวน ข ค่า – 5

สิ่งนี้ทำให้เราได้ผลลัพธ์จาก 0 สำหรับ ยู1.

เราใช้สูตรต่อไปที่จะเกิดขึ้นกับ ยู2:

ยู2 = R x W พอควร Q

ลองป้อนหมายเลขของเรา:

ยู2 = 3 x 3 mod 5

ยู2 = 9 mod 5

จากนั้นเรามุ่งหน้ากลับไปที่เครื่องคิดเลขแบบโมดูโลปกติโดยใช้พารามิเตอร์เดียวกันกับก่อนหน้านี้ยกเว้น:

• จำนวน ค่า – 9
• จำนวน ข ค่า – 5

หากคุณป้อนอย่างถูกต้องมันจะให้ผลลัพธ์แก่คุณ ยู2 ของ 4.

ตอนนี้เรามีค่าของเราสำหรับ ยู1 และ ยู2, เราสามารถหา โวลต์, ด้วยสูตรดังต่อไปนี้:

v = (ก.u1Yu2 พอควร พี) mod Q

มาโยนตัวเลขของเรา:

โวลต์ = (90 x 44 mod 11) mod 5

โวลต์ = (1 x 256 mod 11) mod 5

โวลต์ = (256 mod 11) mod 5

เรากลับไปที่เครื่องคำนวณโมดูโลแบบปกติโดยใช้พารามิเตอร์เดียวกันกับก่อนหน้านี้ยกเว้น:

• จำนวน ค่า – 256
• จำนวน ข ค่า – 11

สิ่งนี้ทำให้เราได้ผลลัพธ์จาก 3. ดังนั้น:

โวลต์ = 3 mod 5

จากนั้นเราใช้เครื่องคิดเลขแบบโมดูโลปกติหนึ่งครั้งสุดท้ายอีกครั้งด้วยพารามิเตอร์เดียวกันยกเว้น:

• จำนวน ค่า – 256
• จำนวน ข ค่า – 11

สิ่งนี้ทำให้เราได้ผลลัพธ์ โวลต์ ของ 3.

หากข้อความเป็นข้อความจริงและไม่ได้รับการแก้ไข v จะเท่ากับ r:

    v = 3

    r = 3

    3 = 3

ดังนั้นข้อความถูกส่งโดยเจ้าของคีย์ส่วนตัวและข้อความไม่ได้ถูกแก้ไขตั้งแต่มันถูกเซ็นชื่อ.

ข้อดีของ DSA & ข้อเสีย

ความปลอดภัยของ DSA นั้นขึ้นอยู่กับว่ามันใช้ตัวเลขที่เพียงพอหรือไม่ นอกจาก p, q และ ก. ปฏิบัติตามพารามิเตอร์ที่ถูกต้องค่าของ k ยังต้องสุ่ม ไม่ควรเป็นค่าที่คาดเดาได้หรือค่าที่ใช้หลายครั้ง หากไม่เป็นไปตามข้อกำหนดเหล่านี้ผู้โจมตีสามารถเรียกคืนกุญแจได้.

แม้จะมีความเป็นไปได้นี้, โดยทั่วไปถือว่ามีความปลอดภัย DSA ตราบใดที่มีการนำไปใช้อย่างถูกต้องและใช้ค่าที่เพียงพอ. แม้ว่าจะค่อนข้างปลอดภัย แต่ DSA ก็ไม่ได้มีแนวโน้มที่จะนำมาใช้มากนักเมื่อเทียบกับ RSA หรือวิธีการเซ็นชื่อแบบดิจิทัลอื่น ๆ เมื่อเปรียบเทียบกับ RSA มันสามารถสร้างคีย์ได้เร็วขึ้นและเร็วขึ้นในการสร้างลายเซ็นดิจิทัล แต่ช้ากว่าเมื่อตรวจสอบได้.

เวอร์ชัน 7.0 ของ OpenSSH หยุดการสนับสนุนคีย์ DSA โดยค่าเริ่มต้นซึ่งเป็นสัญญาณว่าโลกกำลังเคลื่อนผ่าน DSA ที่ผ่านมาและไปสู่อัลกอริธึมอื่น ๆ.

ECDSA & EdDSA

RSA และ DSA ไม่ใช่อัลกอริธึมลายเซ็นดิจิตอลเพียงอย่างเดียวและไม่เหมาะสำหรับทุกสถานการณ์ มีช่วงอื่น ๆ เช่น ECDSA และ EdDSA, ซึ่งมีคุณสมบัติที่ทำให้เป็นที่นิยมในบางสถานการณ์.

น่าเสียดายที่สิ่งเหล่านี้ขึ้นอยู่กับคณิตศาสตร์ที่ซับซ้อนยิ่งขึ้นเช่นเส้นโค้งรูปไข่และการเข้ารหัสเส้นโค้ง Edwards เราจะไม่ครอบคลุมรายละเอียดในวันนี้เนื่องจากความซับซ้อนที่เพิ่มขึ้นนี้ แต่เราจะพูดถึงข้อดีและข้อเสียที่อาจเกิดขึ้น.

ECDSA

อัลกอริทึมลายเซ็นดิจิตอล Elliptic Curve เป็นรูปแบบของ DSA ที่รวมการเข้ารหัสแบบวงรีรูปไข่ มันให้ระดับความปลอดภัยที่คล้ายกับ RSA แต่มีคีย์ที่เล็กกว่ามาก สิ่งนี้ทำให้มีประสิทธิภาพมากกว่า RSA หรือ DSA ในด้านประสิทธิภาพส่วนใหญ่.

EdDSA

นี่เป็นอีกทางเลือกหนึ่งของ DSA ยกเว้นว่าจะขึ้นอยู่กับเส้นโค้ง Twisted Edwards มันค่อนข้างใหม่เท่าที่ขั้นตอนวิธีไปซึ่งมีทั้งข้อดีและข้อเสีย ในด้านบวกจะใช้เทคนิคใหม่ที่เพิ่มประสิทธิภาพ.

น่าเสียดายที่อัลกอรึทึมที่ใหม่กว่านั้นยังไม่ได้รับการตรวจสอบอย่างละเอียดมากนักดังนั้นหลายคนจึงระมัดระวังเมื่อตัดสินใจว่าจะใช้งานหรือไม่.

อย่างไรก็ตามเรื่องนี้การใช้ EdDSA มอบประสิทธิภาพระดับสูง, ความต้านทานต่อการโจมตีช่องทางด้านข้างและไม่จำเป็นต้องมีหมายเลขสุ่มเฉพาะในแต่ละลายเซ็น ในขั้นตอนนี้ EdDSA ดูมีแนวโน้มและเริ่มเห็นการใช้งานที่กว้างขึ้น แต่เราจะต้องรอดูว่าการศึกษาในอนาคตจะพบช่องโหว่ด้านความปลอดภัยหรือไม่.

ใบรับรองดิจิทัล

ทุกคนสามารถสร้างคู่คีย์ได้อย่างง่ายดายแม้แต่ผู้โจมตี ดังนั้นสิ่งที่ทำให้ใครบางคนจากการทำพวงกุญแจและแกล้งทำเป็นว่าพวกเขาเป็นประธานาธิบดีหรือวางตัวเป็นคนอื่น?

ไม่มีอะไรจะหยุดใครบางคนจากการอ้างว่าพวกเขาเป็นคนอื่น แต่มีระบบในสถานที่ที่อนุญาตให้ผู้อื่นตรวจสอบว่าบุคคลนั้นเป็นผู้ที่พวกเขาอ้างว่าเป็นจริงหรือไม่ มันถูกเรียกว่า โครงสร้างพื้นฐานกุญแจสาธารณะ (PKI), และมันเกี่ยวข้องกับ ใบรับรองดิจิทัลที่เชื่อมโยงกุญแจสาธารณะของบุคคลหรือนิติบุคคลกับตัวตนที่แท้จริงของพวกเขา. ใบรับรองเหล่านี้ลงนามโดยผู้อื่นเพื่อระบุจำนวนใบรับรองที่ควรเชื่อถือได้.

คุณสามารถเปรียบเทียบกระบวนการกับการใช้พรักานในการตรวจสอบเอกสาร หากใครบางคนมีสำเนาสูติบัตรคุณอาจสงสัยว่าถูกต้องหรือไม่ หากสูติบัตรเดียวกันนั้นลงนามและประทับตราโดยทนายความคุณจะมีแนวโน้มที่จะเชื่อว่าเป็นสำเนาจริง.

ทำไม?

เนื่องจากลายเซ็นและตราประทับแสดงให้เห็นว่าหน่วยงานสาธารณะที่เชื่อถือได้เห็นบุคคลและใบรับรองการเกิดดั้งเดิมของพวกเขาจากนั้นตรวจสอบว่าสำเนาถูกต้องตามกฎหมาย ทนายความตรวจสอบความถูกต้องของสำเนาสูติบัตรและเดิมพันชื่อเสียงของพวกเขาด้านหลังด้วยลายเซ็นและตราประทับของพวกเขา.

ความไว้วางใจที่เรามีต่อทนายความจะถูกโอนไปยังสำเนาสูติบัตรทำให้เราเชื่อใจได้มากกว่าหนึ่งซึ่งไม่ได้รับการรับรอง.

การรับรองมีสองประเภทใหญ่ ๆ cหน่วยงานผู้ออกใบรับรอง (CA) และเว็บที่เชื่อถือได้.

ผู้ออกใบรับรอง

ผู้ออกใบรับรองคือ องค์กรที่เชื่อถือได้ซึ่งเรียกใช้การตรวจสอบบุคคลหรือนิติบุคคลเพื่อตรวจสอบว่าพวกเขาเป็นเจ้าของที่ถูกต้องของคีย์สาธารณะ. หากการตรวจสอบแสดงให้เห็นว่าบุคคลนั้นเป็นเจ้าของที่แท้จริงหน่วยงานผู้ออกใบรับรองจะลงนามใบรับรองด้วยรหัสของตัวเองซึ่งแสดงว่าการตรวจสอบเสร็จสมบูรณ์และเชื่อว่าการเชื่อมโยงของบุคคลและกุญแจสาธารณะนั้นถูกต้องตามกฎหมาย.

ตราบใดที่เราเชื่อถือหน่วยงานผู้ออกใบรับรองและกระบวนการตรวจสอบความถูกต้องของคีย์จากนั้นเราสามารถเชื่อถือใบรับรองที่ลงนามโดยพวกเขา, และทำให้คีย์สาธารณะแสดงถึงบุคคลนั้นอย่างแท้จริง.

ขึ้นอยู่กับประเภทของใบรับรองและแอปพลิเคชันระดับต่าง ๆ สามารถมีกระบวนการตรวจสอบที่แตกต่างกันดังนั้นจึงเป็นตัวแทนระดับความน่าเชื่อถือที่สูงขึ้นหรือต่ำลง.

เว็บแห่งความไว้วางใจ

เว็บแห่งความน่าเชื่อถือดำเนินงานภายใต้สถานที่เดียวกันยกเว้น tที่นี่ไม่มีหน่วยงานกลาง เช่นผู้ออกใบรับรองที่ทำกระบวนการตรวจสอบและลงนามใบรับรอง.

แต่เว็บแห่งความไว้วางใจนั้นอาศัยบุคคลอื่น ๆ เพื่อลงนามใบรับรองโดยวางเดิมพันชื่อเสียงในลิงก์ระหว่างบุคคลและรหัสสาธารณะ ระบบนี้ส่วนใหญ่จะใช้กับ PGP ซึ่งผู้ใช้สามารถสร้างใบรับรองของตนเองได้อย่างง่ายดาย.

มันทำงานได้เช่นนี้:

สมมติว่าคุณมีเพื่อนสองคนที่ต้องการลงชื่อใบรับรองเพื่อพิสูจน์ว่าพวกเขาเป็นเจ้าของที่ถูกต้องตามกฎหมายของกุญแจสาธารณะนั้น ๆ คุณรู้จักคนเหล่านี้เป็นอย่างดีและพวกเขาแสดงรหัสรัฐบาลของพวกเขาซึ่งทำให้คุณมั่นใจอย่างแน่นอนว่าพวกเขาคือคนที่พวกเขาบอกว่าพวกเขาเป็นใครและเป็นเจ้าของที่แท้จริงของกุญแจสาธารณะที่พวกเขาอ้างสิทธิ์.

เนื่องจากคุณรู้ว่าพวกเขาเป็นเจ้าของที่ถูกต้องตามกฎหมายของกุญแจสาธารณะของพวกเขาคุณมีความสุขที่จะใช้กุญแจส่วนตัวของคุณเพื่อลงนามในใบรับรองของพวกเขา, staking ชื่อเสียงของคุณกับพวกเขาและเป็นหลักพูดว่า “ใช่ พวกเขาอ้างว่าเป็น” เพื่อนสองคนนี้สามารถทำสิ่งเดียวกันกับคุณได้.

สมมติว่าเพื่อนสองคนของคุณแต่ละคนมีเพื่อนอีกสองคนที่ต้องการลงชื่อใบรับรอง หากเพื่อนของคุณสองคนลงนามใบรับรองอื่น ๆ เหล่านี้คุณสามารถใช้ความเชื่อมั่นที่คุณมีในเพื่อนของคุณเพื่อยอมรับว่าคนอื่น ๆ เหล่านี้เป็นคนที่พวกเขาบอกว่าพวกเขาเป็นอย่างแท้จริง.

จากนั้นเพื่อนของเพื่อนของคุณสามารถลงชื่อใบรับรองของคนที่พวกเขาเชื่อถือได้และในที่สุดก็สร้างเครือข่ายขนาดใหญ่ของบุคคลที่เชื่อถือได้ เมื่อเว็บเหล่านี้มีขนาดใหญ่พอและเชื่อมต่อกับเว็บอื่นได้แล้ว, พวกเขาสามารถใช้เป็นวิธีการที่เชื่อถือคนอื่นในเครือข่าย.

ยิ่งลายเซ็นบนใบรับรองโดยเฉพาะถ้าเป็นลายเซ็นจากบุคคลที่เชื่อถือได้สูง, ยิ่งคุณสามารถเชื่อถือใบรับรองดิจิทัลของใครบางคนและลิงก์ระหว่างกุญแจสาธารณะและตัวตนของพวกเขา.

ผู้ใช้ PGP มักจะจัดงานปาร์ตี้เซ็นชื่อที่สำคัญซึ่งผู้คนรวมตัวกันเพื่อตรวจสอบข้อมูลประจำตัวและลงนามใบรับรองดิจิทัล การชุมนุมเหล่านี้ช่วยนำผู้คนใหม่เข้าสู่เครือข่าย.

แม้ว่ามันจะมาพร้อมกับความซับซ้อนบางอย่าง แต่ข้อดีของเว็บของระบบความน่าเชื่อถือก็คือไม่มีหน่วยงานกลางที่สามารถเสียหายได้.

มีลายเซ็นดิจิทัลที่ปลอดภัย?

ในความหมายทั่วไป, ลายเซ็นดิจิทัลมีความปลอดภัยเว้นแต่ว่าคีย์ส่วนตัวของผู้รับได้รับอันตราย. หากเจ้าของแจ้งให้บุคคลอื่นฝากกุญแจส่วนตัวที่ถูกเขียนลงไปหรือถูกขโมยไปในทางอื่นก็เป็นไปได้ที่ผู้โจมตีจะสามารถเซ็นข้อความด้วยระบบดิจิตอลเสมือนว่าพวกเขาเป็นเจ้าของ.

สิ่งนี้สามารถนำไปสู่การโจมตีของปลอมแปลงเหยื่อหรือแก้ไขข้อมูลของพวกเขา นี่เป็นปัญหาด้านความปลอดภัยที่ยิ่งใหญ่และใครก็ตามที่สงสัยว่ากุญแจของพวกเขาถูกบุกรุกจะต้องเพิกถอนใบรับรองดิจิทัลที่เชื่อมโยงพวกเขากับกุญแจสาธารณะของพวกเขาและได้ออกใบรับรองใหม่.

มีข้อแม้อื่น ๆ อีกเล็กน้อยเมื่อพูดถึงความปลอดภัยของลายเซ็นดิจิทัล ควรใช้อัลกอริธึมลายเซ็นดิจิทัลที่เหมาะสมและต้องดำเนินการอย่างถูกต้องด้วย นอกจากนี้ยังต้องมีการเชื่อมโยงกุญแจสาธารณะกับเจ้าของโดยทั่วไปผ่านใบรับรองดิจิทัล.

ตราบใดที่ปฏิบัติตามข้อกำหนดเหล่านี้คุณก็จะปฏิบัติตามหลักปฏิบัติที่ดีที่สุดในอุตสาหกรรมและรหัสส่วนตัวของคุณจะไม่ถูกบุกรุก ลายเซ็นดิจิทัลเป็นวิธีที่ยอดเยี่ยมในการมอบความถูกต้องความสมบูรณ์และการปฏิเสธข้อมูล.

ข้อมูลที่มีโครงสร้าง โดย Kai Stachowiak ได้รับใบอนุญาตภายใต้ มอนส์ CC0