การเข้ารหัส RSA คืออะไรและทำงานอย่างไร

การเข้ารหัส RSA เป็นระบบที่แก้ปัญหาที่เคยเป็นหนึ่งในปัญหาที่ใหญ่ที่สุดในการเข้ารหัส: คุณจะส่งข้อความที่เข้ารหัสได้อย่างไร โดยไม่ต้องมีโอกาสแบ่งปันรหัสก่อนหน้ากับพวกเขา?

บทความนี้จะสอนทุกสิ่งที่คุณจำเป็นต้องรู้ วิธีการเข้ารหัส RSA ได้รับการพัฒนา, มันทำงานอย่างไร, คณิตศาสตร์ที่อยู่เบื้องหลัง, มันใช้สำหรับอะไร เช่นเดียวกับบางส่วนของ ปัญหาด้านความปลอดภัยที่ใหญ่ที่สุดที่มันต้องเผชิญ. การเรียนรู้เกี่ยวกับ RSA จะให้ความรู้พื้นฐานที่จะช่วยให้คุณเข้าใจว่าชีวิตออนไลน์ของเรามีความปลอดภัยมากเพียงใด.

การเข้ารหัส RSA คืออะไร?

สมมติว่าคุณต้องการบอกความลับกับเพื่อนของคุณ หากคุณอยู่ติดกับพวกเขาคุณสามารถกระซิบได้ หากคุณอยู่ฝั่งตรงข้ามของประเทศนั่นจะไม่ได้ผลแน่นอน คุณสามารถจดบันทึกและส่งไปยังพวกเขาหรือใช้โทรศัพท์ แต่ ช่องทางการสื่อสารแต่ละช่องเหล่านี้ไม่ปลอดภัย และใครก็ตามที่มีแรงจูงใจมากพอจะสามารถดักจับข้อความได้ง่าย.

หากความลับมีความสำคัญมากพอคุณจะไม่เสี่ยงที่จะเขียนลงไปตามปกติ – สายลับหรือพนักงานไปรษณีย์โกงอาจดูจดหมายของคุณได้ ในทำนองเดียวกันบางคนอาจแตะโทรศัพท์ของคุณโดยที่คุณไม่รู้และบันทึกการโทรทุกครั้งที่คุณโทร.

ทางออกหนึ่งในการป้องกันผู้ดักฟังจากการเข้าถึงเนื้อหาข้อความคือ เข้ารหัสมัน. โดยทั่วไปหมายถึงการเพิ่มรหัสลงในข้อความที่เปลี่ยนเป็นระเบียบที่สับสน หากรหัสของคุณซับซ้อนเพียงพอผู้คนเท่านั้นที่จะสามารถเข้าถึงข้อความต้นฉบับได้คือผู้ที่สามารถเข้าถึงรหัสได้.

หากคุณมีโอกาสที่จะแบ่งปันรหัสกับเพื่อนของคุณก่อนแล้ว คุณสามารถส่งข้อความที่เข้ารหัสได้ตลอดเวลา, รู้ว่าคุณทั้งสองเป็นคนเดียวที่มีความสามารถในการอ่านเนื้อหาข้อความ แต่ถ้าคุณไม่มีโอกาสแชร์รหัสล่วงหน้า?

นี่เป็นหนึ่งในปัญหาพื้นฐานของการเข้ารหัสซึ่งได้รับการแก้ไขโดย รูปแบบการเข้ารหัสคีย์สาธารณะ (หรือเรียกอีกอย่างว่าการเข้ารหัสแบบไม่สมมาตร) เช่น RSA.

ภายใต้การเข้ารหัส RSA ข้อความจะถูกเข้ารหัสด้วยรหัสที่เรียกว่า กุญแจสาธารณะ, ซึ่งสามารถแบ่งปันได้อย่างเปิดเผย เนื่องจากคุณสมบัติทางคณิตศาสตร์ที่แตกต่างกันของอัลกอริทึม RSA, เมื่อข้อความได้รับการเข้ารหัสด้วยกุญแจสาธารณะจะสามารถถอดรหัสได้ด้วยกุญแจอื่นหรือที่รู้จักกันในชื่อไพรเวตคีย์เท่านั้น. ผู้ใช้ RSA แต่ละคนมีคู่ของคีย์ซึ่งประกอบด้วยกุญแจสาธารณะและกุญแจส่วนตัว ตามชื่อที่แนะนำคีย์ส่วนตัวจะต้องถูกเก็บเป็นความลับ.

รูปแบบการเข้ารหัสคีย์สาธารณะแตกต่างจาก การเข้ารหัสคีย์สมมาตรซึ่งทั้งกระบวนการเข้ารหัสและถอดรหัสใช้ไพรเวตคีย์เดียวกัน. ความแตกต่างเหล่านี้ทำให้การเข้ารหัสพับลิกคีย์เช่น RSA มีประโยชน์สำหรับการสื่อสารในสถานการณ์ที่ไม่มีโอกาสแจกจ่ายคีย์อย่างปลอดภัยล่วงหน้า.

อัลกอริธึม – คีย์สมมาตรมีแอปพลิเคชันของตนเองเช่นการเข้ารหัสข้อมูลสำหรับการใช้งานส่วนตัวหรือเมื่อมีแชนเนลที่ปลอดภัยที่คีย์ส่วนตัวสามารถแชร์ได้.

ดูสิ่งนี้ด้วย: การเข้ารหัสคีย์สาธารณะ

ใช้การเข้ารหัส RSA ที่ไหน?

การเข้ารหัส RSA มักใช้ ร่วมกับแผนการเข้ารหัสอื่น ๆ, หรือสำหรับ ลายเซ็นดิจิทัล ซึ่งสามารถพิสูจน์ความถูกต้องและความสมบูรณ์ของข้อความ โดยทั่วไปจะไม่ใช้ในการเข้ารหัสข้อความหรือไฟล์ทั้งหมดเนื่องจากมีประสิทธิภาพน้อยกว่าและใช้ทรัพยากรจำนวนมากกว่าการเข้ารหัสแบบ symmetric-key.

เพื่อทำให้สิ่งต่าง ๆ มีประสิทธิภาพมากขึ้น, โดยทั่วไปไฟล์จะถูกเข้ารหัสด้วยอัลกอริทึมแบบ symmetric-key จากนั้นคีย์ symmetric จะถูกเข้ารหัสด้วยการเข้ารหัส RSA. ภายใต้กระบวนการนี้เฉพาะเอนทิตีที่สามารถเข้าถึงคีย์ส่วนตัวของ RSA เท่านั้นที่จะสามารถถอดรหัสคีย์สมมาตรได้.

โดยไม่สามารถเข้าถึงคีย์สมมาตร ไฟล์ต้นฉบับไม่สามารถถอดรหัสได้. วิธีนี้สามารถใช้เพื่อรักษาข้อความและไฟล์ให้ปลอดภัยโดยไม่ต้องใช้เวลานานเกินไปหรือใช้ทรัพยากรการคำนวณมากเกินไป.

การเข้ารหัส RSA สามารถใช้ในระบบที่แตกต่างกันจำนวนหนึ่ง มันสามารถนำมาใช้ใน OpenSSL, wolfCrypt, cryptlib และจำนวนของห้องสมุดเข้ารหัสลับอื่น ๆ.

ในฐานะที่เป็นหนึ่งในแผนการเข้ารหัสลับรหัสสาธารณะที่ใช้กันอย่างแพร่หลาย RSA ได้วางรากฐานสำหรับการสื่อสารที่ปลอดภัยของเรา มันเป็น ใช้แบบดั้งเดิมใน TLS และยังเป็นอัลกอริทึมดั้งเดิมที่ใช้ในการเข้ารหัส PGP RSA ยังคงมีให้เห็นในเว็บเบราว์เซอร์อีเมล VPN แชทและช่องทางการสื่อสารอื่น ๆ.

RSA มักใช้ในการเชื่อมต่อที่ปลอดภัยระหว่างไคลเอนต์ VPN และเซิร์ฟเวอร์ VPN ภายใต้โปรโตคอลเช่น OpenVPN การจับมือ TLS สามารถใช้อัลกอริทึม RSA เพื่อแลกเปลี่ยนคีย์และสร้างแชนเนลที่ปลอดภัย.

พื้นหลังของการเข้ารหัส RSA

ดังที่เราได้กล่าวถึงในตอนเริ่มต้นของบทความนี้ก่อนการเข้ารหัสคีย์สาธารณะมันเป็นความท้าทายในการสื่อสารอย่างปลอดภัยหากไม่มีโอกาสแลกเปลี่ยนกุญแจอย่างปลอดภัยก่อน หากไม่มีโอกาสแบ่งปันรหัสล่วงหน้าหรือช่องทางที่ปลอดภัยซึ่งสามารถแจกจ่ายกุญแจได้ไม่มีทางสื่อสารโดยไม่มีการคุกคามจากศัตรูที่สามารถดักจับและเข้าถึงเนื้อหาข้อความได้.

มันไม่ใช่จนกระทั่งปี 1970 ที่สิ่งต่าง ๆ เริ่มเปลี่ยนไป การพัฒนาครั้งแรกที่สำคัญต่อสิ่งที่เราเรียกว่าการเข้ารหัสแบบพับลิกคีย์ได้รับการเผยแพร่เมื่อต้นทศวรรษโดย James H. Ellis เอลลิสไม่สามารถหาวิธีที่จะนำผลงานของเขาไปใช้ได้ แต่เพื่อนร่วมงานของเขาก็ขยายตัวมากขึ้นเมื่อ Clifford Cocks กลายเป็นสิ่งที่เรารู้กันในตอนนี้ การเข้ารหัส RSA.

ชิ้นส่วนสุดท้ายของตัวต่อคือสิ่งที่เราเรียกว่า การแลกเปลี่ยนคีย์ Diffie-Hellman. Malcolm J. Williamson ผู้ร่วมงานอีกคนหนึ่งได้คิดหารูปแบบที่อนุญาตให้ทั้งสองฝ่ายแบ่งปันคีย์การเข้ารหัสแม้ว่าช่องสัญญาณจะถูกตรวจสอบโดยฝ่ายตรงข้าม.

งานทั้งหมดนี้ดำเนินการที่สำนักข่าวกรองแห่งสหราชอาณาจักรซึ่งเป็นที่ทำการสื่อสารของรัฐบาล (GCHQ) ซึ่ง เก็บการค้นพบที่จำแนก. ส่วนหนึ่งเนื่องจากข้อ จำกัด ทางเทคโนโลยี GCHQ ไม่เห็นการใช้รหัสลับสาธารณะในเวลานั้นการพัฒนาจึงนั่งเฉยๆบนชั้นรวบรวมฝุ่น. มันไม่ได้จนกว่าปี 1997 ว่างานถูกยกเลิกการจำแนกประเภทและนักประดิษฐ์ดั้งเดิมของ RSA ได้รับการยอมรับ.

หลายปีต่อมาแนวคิดที่คล้ายกันเริ่มพัฒนาในพื้นที่สาธารณะ Ralph Merkle สร้างรูปแบบแรกของ การเข้ารหัสคีย์สาธารณะ, ซึ่งมีอิทธิพลต่อ Whitfield Diffie และ Martin Hellman ในการออกแบบการแลกเปลี่ยนกุญแจ Diffie-Hellman.

ความคิดของ Diffie และ Hellman หายไปสิ่งสำคัญอย่างหนึ่งที่จะทำให้งานของพวกเขาเป็นรากฐานของการเข้ารหัสคีย์สาธารณะ นี่คือ ฟังก์ชั่นทางเดียวที่ยากต่อการกลับด้าน. ในปี 1977, Ron Rivest, Adi Shamir และ Leonard Adleman, ชื่อสุดท้ายของรูปแบบ RSA ย่อมาจากคำตอบหลังจากหนึ่งปีของการทำงานกับปัญหา.

นักวิชาการจาก MIT ได้ทำการพัฒนาหลังจากปาร์ตี้ปัสกาในปี 1977 หลังจากดื่มคืนหนึ่ง Rivest กลับบ้าน แต่แทนที่จะนอนหลับเขาใช้เวลาช่วงเย็นเขียนหนังสือที่ทำให้ความคิดของเขาเป็นทางการสำหรับฟังก์ชั่นทางเดียวที่จำเป็น.

แนวคิดดังกล่าวได้รับการจดสิทธิบัตรในปี 1983 โดย MIT แต่มันไม่ได้เป็นจนถึงวันแรกของอินเทอร์เน็ตที่อัลกอริทึม RSA เริ่มเห็นการยอมรับอย่างกว้างขวางว่าเป็นเครื่องมือรักษาความปลอดภัยที่สำคัญ.

การเข้ารหัส RSA ทำงานอย่างไร?

ต่อไปนี้จะเป็นเรื่องง่ายเพราะผู้อ่านจำนวนมากอาจมีรอยแผลเป็นจากครูคณิตศาสตร์ระดับมัธยม เพื่อไม่ให้คณิตศาสตร์ออกนอกมือเราจะเป็น ลดความซับซ้อนของแนวคิดและใช้ตัวเลขที่น้อยกว่ามาก. ในความเป็นจริงการเข้ารหัส RSA ใช้ตัวเลขสำคัญที่มีขนาดใหญ่กว่ามากและมีความซับซ้อนอื่น ๆ.

มีแนวคิดที่แตกต่างกันหลายประการที่คุณจะต้องเข้าใจก่อนที่เราจะอธิบายว่ามันเข้ากันได้อย่างไร เหล่านี้ ได้แก่ ฟังก์ชั่นประตูกลสร้างช่วงเวลา, ฟังก์ชั่น Totient ของ Carmichael และกระบวนการแยกต่างหากที่เกี่ยวข้องกับ คำนวณคีย์สาธารณะและส่วนตัว ใช้ในกระบวนการเข้ารหัสและถอดรหัส.

ฟังก์ชั่นประตูกับดัก

การเข้ารหัส RSA ทำงานภายใต้สมมติฐานว่าอัลกอริทึมนั้น ง่ายต่อการคำนวณในทิศทางเดียว แต่แทบจะเป็นไปไม่ได้ในทางกลับกัน. ตัวอย่างเช่นหากคุณได้รับแจ้งว่า 701,111 เป็นผลผลิตของตัวเลขสองตัวคุณจะสามารถคิดได้ว่าตัวเลขสองตัวนั้นคืออะไร?

แม้จะมีเครื่องคิดเลขหรือคอมพิวเตอร์พวกเราส่วนใหญ่ก็ยังไม่รู้ว่าจะเริ่มจากตรงไหนให้คนเดียวสามารถหาคำตอบได้ แต่ถ้าเราพลิกสิ่งต่าง ๆ มันจะง่ายขึ้นมาก ผลลัพธ์ของ:

907 x 773

หากคุณเบื่อพอคุณจะสามารถตีโทรศัพท์ของคุณหรืออาจคำนวณในหัวของคุณเพื่อค้นหาว่าคำตอบคือ 701,111 ที่กล่าวถึงก่อนหน้านี้ 907 และ 773 นี้เป็นตัวเลขเฉพาะที่ตอบคำถามแรกของเราซึ่งแสดงให้เราเห็นว่าสมการบางอย่างสามารถหาทางเดียวได้ แต่ดูเหมือนจะเป็นไปไม่ได้ในทางกลับกัน.

อีกแง่มุมที่น่าสนใจของสมการนี้คือมันง่ายที่จะหาหนึ่งในจำนวนเฉพาะถ้าคุณมีอีกหนึ่งรวมทั้งผลิตภัณฑ์ หากคุณได้รับแจ้งว่า 701,111 เป็นผลลัพธ์ของ 907 คูณด้วยจำนวนเฉพาะอีกตัวหนึ่งคุณสามารถหานายกอื่นด้วยสมการต่อไปนี้:

701,111 ÷ 907 = 773

เนื่องจากความสัมพันธ์ระหว่างตัวเลขเหล่านี้ง่ายต่อการคำนวณในทิศทางเดียว แต่กลับยากอย่างไม่น่าเชื่อสมการจึงเป็นที่รู้จักกันในชื่อ ฟังก์ชั่นประตูกับดัก. โปรดทราบว่าในขณะที่ตัวอย่างข้างต้นนั้นยากสำหรับคนที่จะคิดออกคอมพิวเตอร์สามารถดำเนินการในระยะเวลาเล็กน้อย.

ด้วยเหตุนี้ RSA จึงใช้ตัวเลขที่มากกว่านี้ ขนาดของจำนวนเฉพาะในการนำไปใช้งานจริงของ RSA นั้นแตกต่างกันไป แต่ในปี 2048 บิตพวกเขาจะรวมตัวกันเพื่อสร้างกุญแจที่มีความยาว 617 หลัก เพื่อช่วยให้คุณมองเห็นภาพได้รหัสจะมีขนาดเท่านี้:

99999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999999

สร้างช่วงเวลา

ฟังก์ชั่นประตูกับดักที่กล่าวถึงข้างต้นเป็นพื้นฐานสำหรับการทำงานของรูปแบบการเข้ารหัสคีย์สาธารณะและส่วนตัว. คุณสมบัติของพวกเขาอนุญาตให้ใช้กุญแจสาธารณะร่วมกันโดยไม่ทำอันตรายต่อข้อความหรือเปิดเผยรหัสส่วนตัว. พวกเขายังอนุญาตให้มีการเข้ารหัสข้อมูลด้วยคีย์เดียวในวิธีที่สามารถถอดรหัสโดยคีย์อื่นจากคู่.

ขั้นตอนแรกของการเข้ารหัสข้อความด้วย RSA คือ สร้างกุญแจ. ในการทำเช่นนี้เราต้องการ ตัวเลขสองตัวที่สำคัญ (พี และ Q) ซึ่งถูกเลือกด้วยการทดสอบเบื้องต้น การทดสอบแบบดั้งเดิมนั้นเป็นอัลกอริทึมที่สามารถค้นหาจำนวนเฉพาะได้อย่างมีประสิทธิภาพเช่นการทดสอบแบบดั้งเดิมของ Rabin-Miller.

ตัวเลขสำคัญใน RSA จะต้องมีขนาดใหญ่มากและค่อนข้างห่างกันมาก ตัวเลขที่เล็กหรือใกล้กันมากจะแตกง่ายขึ้น อย่างไรก็ตามเรื่องนี้ตัวอย่างของเราจะใช้ตัวเลขที่น้อยลงเพื่อให้ง่ายต่อการติดตามและคำนวณ.

สมมติว่าการทดสอบแบบดั้งเดิมให้ตัวเลขที่สำคัญที่เราใช้ด้านบน 907 และ 773 ขั้นตอนต่อไปคือการค้นพบโมดูลัสn) ใช้สูตรต่อไปนี้:

n = พี x Q

ที่ไหน พี = 907 และ Q = 773

ดังนั้น:

n = 907 x 773

n = 701,111

ฟังก์ชั่น Totient ของ Carmichael

เมื่อเรามี n, เราใช้ ฟังก์ชั่นทั้งหมดของ Carmichael:

    λ(n) = LCM (พี – 1, Q – 1)

หากผ่านไปสักพักหนึ่งหลังจากที่คุณอ่านตำราคณิตศาสตร์สิ่งต่างๆข้างต้นอาจดูน่ากลัวนิดหน่อย คุณสามารถข้ามส่วนนี้และเพียงแค่เชื่อมั่นว่าการคำนวณทางคณิตศาสตร์นั้นไม่เช่นนั้นเราจะทำการคำนวณอีกเล็กน้อย ทุกอย่างจะถูกอธิบายในรายละเอียดให้มากที่สุดเท่าที่จะเป็นไปได้เพื่อช่วยให้คุณได้รับข้อมูลเบื้องต้น.

สำหรับผู้ที่ไม่ทราบ, λ (n) แสดงถึงผลรวมของ Carmichael สำหรับ n, ในขณะที่ LCM หมายถึงตัวคูณร่วมน้อย, ซึ่งเป็นจำนวนที่ต่ำที่สุดที่ทั้งคู่ พี และ Q สามารถแบ่งออกเป็น มีวิธีที่แตกต่างกันไม่กี่อย่างในการค้นหาสิ่งนี้ แต่วิธีที่ง่ายที่สุดคือการเชื่อถือเครื่องคิดเลขออนไลน์เพื่อทำสมการให้คุณ ดังนั้นให้เราใส่ตัวเลขลงในสมการ:

    λ(701111) = LCM (907 – 1, 773 – 1)

    λ(701111) = LCM (906, 772)

   ด้วยการใช้เครื่องคิดเลขที่ลิงก์ข้างบนสิ่งนี้ทำให้เรา

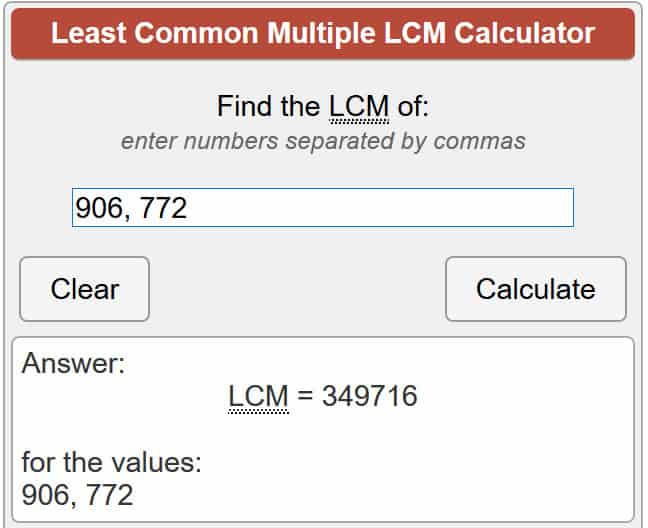
    λ(701111) = 349,716

สร้างกุญแจสาธารณะ

ตอนนี้เรามียอดรวมของจำนวนเฉพาะของ Carmichael แล้ว ได้เวลาคิดกุญแจสาธารณะของเราแล้ว. ภายใต้ RSA, กุญแจสาธารณะถูกสร้างขึ้นจากจำนวนเฉพาะ อี, เช่นกัน n. จำนวน อี สามารถเป็นอะไรก็ได้ระหว่าง 1 ถึงค่า λ(n) ซึ่งในตัวอย่างของเราคือ 349,716.

เนื่องจากรหัสสาธารณะถูกเปิดเผยอย่างเปิดเผยจึงไม่สำคัญสำหรับ อี เพื่อเป็นตัวเลขสุ่ม ในทางปฏิบัติ, อี โดยทั่วไปตั้งไว้ที่ 65537, เพราะเมื่อมีการสุ่มเลือกตัวเลขจำนวนมากมันจะทำให้การเข้ารหัสมีประสิทธิภาพน้อยลง สำหรับตัวอย่างของวันนี้เราจะทำให้ตัวเลขมีขนาดเล็กเพื่อให้การคำนวณมีประสิทธิภาพ สมมติว่า:

อี = 11

ข้อมูลที่เข้ารหัสสุดท้ายของเราเรียกว่า ciphertext (ค) เราได้รับมาจากข้อความธรรมดาของเรา (ม.) โดยใช้คีย์สาธารณะด้วยสูตรต่อไปนี้:

ค = ม.อี mod n

เราได้เกิดขึ้นแล้ว อี และเรารู้ n เช่นกัน สิ่งเดียวที่เราต้องอธิบายคือ พอควร. บทความนี้ค่อนข้างลึก แต่ก็อ้างถึง การทำงานแบบโมดูโล, ซึ่งก็หมายถึงส่วนที่เหลือที่เหลืออยู่เมื่อคุณแบ่งด้านหนึ่งโดยด้านอื่น ตัวอย่างเช่น:

10 พอควร 3 = 1

นี่เป็นเพราะ 3 เข้าสู่ 10 สามครั้งโดยที่เหลือ 1.

กลับไปที่สมการของเรา เพื่อให้สิ่งต่าง ๆ เรียบง่ายสมมติว่าอย่างนั้น ข้อความ (ม.) ที่เราต้องการเข้ารหัสและเก็บเป็นความลับเป็นเพียงหมายเลขเดียว, 4. มาเสียบทุกอย่างใน:

ค = ม.อี พอควร n

ค = 411 พอควร 701111

ค = 4,194,304 พอควร 701111

อีกครั้งเพื่อให้ การทำงานแบบโมดูโล ง่าย ๆ เราจะใช้เครื่องคิดเลขออนไลน์ แต่คุณสามารถคิดออกเองได้ ด้วยการป้อน 4,194,304 ลงในเครื่องคิดเลขออนไลน์มันทำให้เรา:

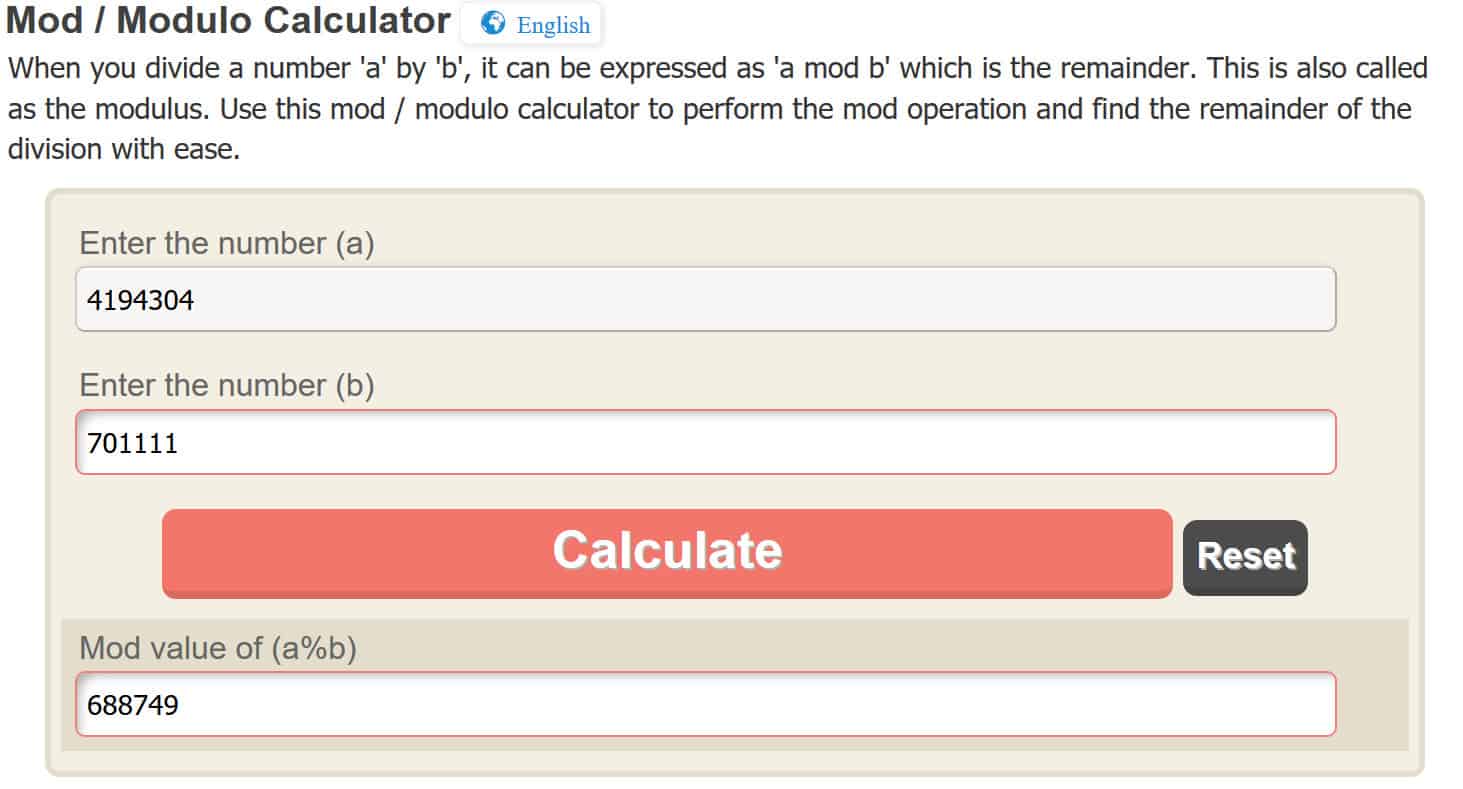
c = 688,749

ดังนั้นเมื่อเราใช้ RSA ในการเข้ารหัสข้อความของเรา, 4, ด้วยรหัสสาธารณะของเรามันทำให้เรา ไซเฟอร์เท็กซ์ของ 688,749. ขั้นตอนก่อนหน้าอาจดูเหมือนหนักเกินไป แต่ก็สำคัญที่จะต้องย้ำสิ่งที่เกิดขึ้นจริง.

เรามี ข้อความจาก 4, ซึ่งเราต้องการเก็บเป็นความลับ เราใช้กุญแจสาธารณะกับกุญแจซึ่งทำให้เรา ผลลัพธ์ที่เข้ารหัสของ 688,749. ตอนนี้มันถูกเข้ารหัส, เราสามารถส่งหมายเลข 688,749 ไปให้เจ้าของกุญแจได้อย่างปลอดภัย. พวกเขาเป็นคนเดียวเท่านั้นที่จะสามารถถอดรหัสได้ด้วยรหัสส่วนตัวของพวกเขา เมื่อพวกเขาถอดรหัสพวกเขาจะเห็นข้อความที่เราส่งจริงๆ, 4.

การสร้างคีย์ส่วนตัว

ในการเข้ารหัส RSA เมื่อข้อมูลหรือข้อความถูกเปลี่ยนเป็น ciphertext ด้วยรหัสสาธารณะจะสามารถถอดรหัสได้โดยกุญแจส่วนตัวจากคู่คีย์เดียวกันเท่านั้น. คีย์ส่วนตัวประกอบด้วย d และ n. เรารู้อยู่แล้ว n, และใช้สมการต่อไปนี้เพื่อค้นหา d:

d = 1 /อี mod λ(n)

ใน สร้างกุญแจสาธารณะ ส่วนด้านบนเราได้ตัดสินใจแล้วว่าในตัวอย่างของเรา, อี จะเท่ากับ 11 ในทำนองเดียวกันเรารู้ว่า λ(n) เท่ากับ 349,716 จากการทำงานก่อนหน้าของเราภายใต้ ฟังก์ชั่น Totient ของ Carmichael. สิ่งต่าง ๆ มีความซับซ้อนเพิ่มขึ้นเล็กน้อยเมื่อเราเจอส่วนนี้ของสูตร:

1 /อี พอควร

สมการนี้อาจดูเหมือนว่าขอให้คุณหาร 1 ด้วย 11 แต่นั่นไม่ใช่กรณี แต่นี่เป็นเพียงสัญลักษณ์ที่เราจำเป็นต้องคำนวณ โมดูลผกผัน ของ อี (ซึ่งในกรณีนี้คือ 11) และ λ(n) (ซึ่งในกรณีนี้คือ 349,716).

สิ่งนี้หมายความว่า แทนที่จะทำการโมดูโลแบบมาตรฐานเราจะใช้อินเวอร์สแทน. โดยปกติแล้วจะพบกับอัลกอริทึม Extended Euclidean แต่มันอยู่นอกขอบเขตเล็กน้อยของบทความนี้ดังนั้นเราจะโกงและใช้เครื่องคิดเลขออนไลน์แทน ตอนนี้เราเข้าใจทุกอย่างที่เกิดขึ้นแล้วให้เสียบข้อมูลของเราเข้ากับสูตร

d = 1 /11 พอควร 349716

ในการดำเนินการนี้ให้ป้อน 11 (หรือค่าใด ๆ ที่คุณอาจมี อี หากคุณพยายามทำสิ่งนี้ด้วยตัวอย่างของคุณเอง) ซึ่งมันบอกว่า จำนวนเต็ม และ 349,716 (หรือค่าใด ๆ ที่คุณอาจมี λ(n) ถ้าคุณพยายามทำสิ่งนี้ด้วยตัวอย่างของคุณเอง) ซึ่งมันบอกว่า modulo ในเครื่องคิดเลขออนไลน์ที่เชื่อมโยงด้านบน หากคุณทำอย่างถูกต้องคุณควรได้รับผลที่:

d = 254, 339

ตอนนี้เรามีค่าสำหรับ d, เราสามารถถอดรหัสข้อความที่เข้ารหัสด้วยกุญแจสาธารณะของเราโดยใช้สูตรต่อไปนี้:

ม. = คd mod n

ตอนนี้เราสามารถกลับไปที่ไซเฟอร์เท็กซ์ที่เราเข้ารหัสภายใต้ การสร้างคีย์ส่วนตัว มาตรา. เมื่อเราเข้ารหัสข้อความด้วยรหัสสาธารณะมันทำให้เรามีค่าสำหรับ ค จาก 688,749. จากด้านบนเรารู้ว่า d เท่ากับ 254,339. เราก็รู้ว่า n เท่ากับ 701,111. สิ่งนี้ทำให้เรา:

ม. = 688,749254339 พอควร 701111.

ดังที่คุณอาจสังเกตเห็นว่าการพยายามใช้ตัวเลขเป็นกำลัง 254,339 อาจมีค่าเล็กน้อยสำหรับเครื่องคิดเลขทั่วไปส่วนใหญ่ แต่เราจะใช้เครื่องคำนวณการถอดรหัส RSA ออนไลน์ หากคุณต้องการใช้วิธีอื่นคุณจะต้องใช้พลังตามปกติและดำเนินการโมดูลัสเหมือนกับวิธีที่เราทำ สร้างกุญแจสาธารณะ มาตรา.

ในเครื่องคิดเลขที่ลิงก์ด้านบนให้ป้อน 701,111 ตำแหน่งที่ระบุ อุปทานโมดูลัส: N, 254,399 ที่มันบอกว่า รหัสถอดรหัส: D, และ 688,749 ที่มันบอกว่า Ciphertext Message ในรูปแบบตัวเลข, ที่แสดงด้านล่าง:

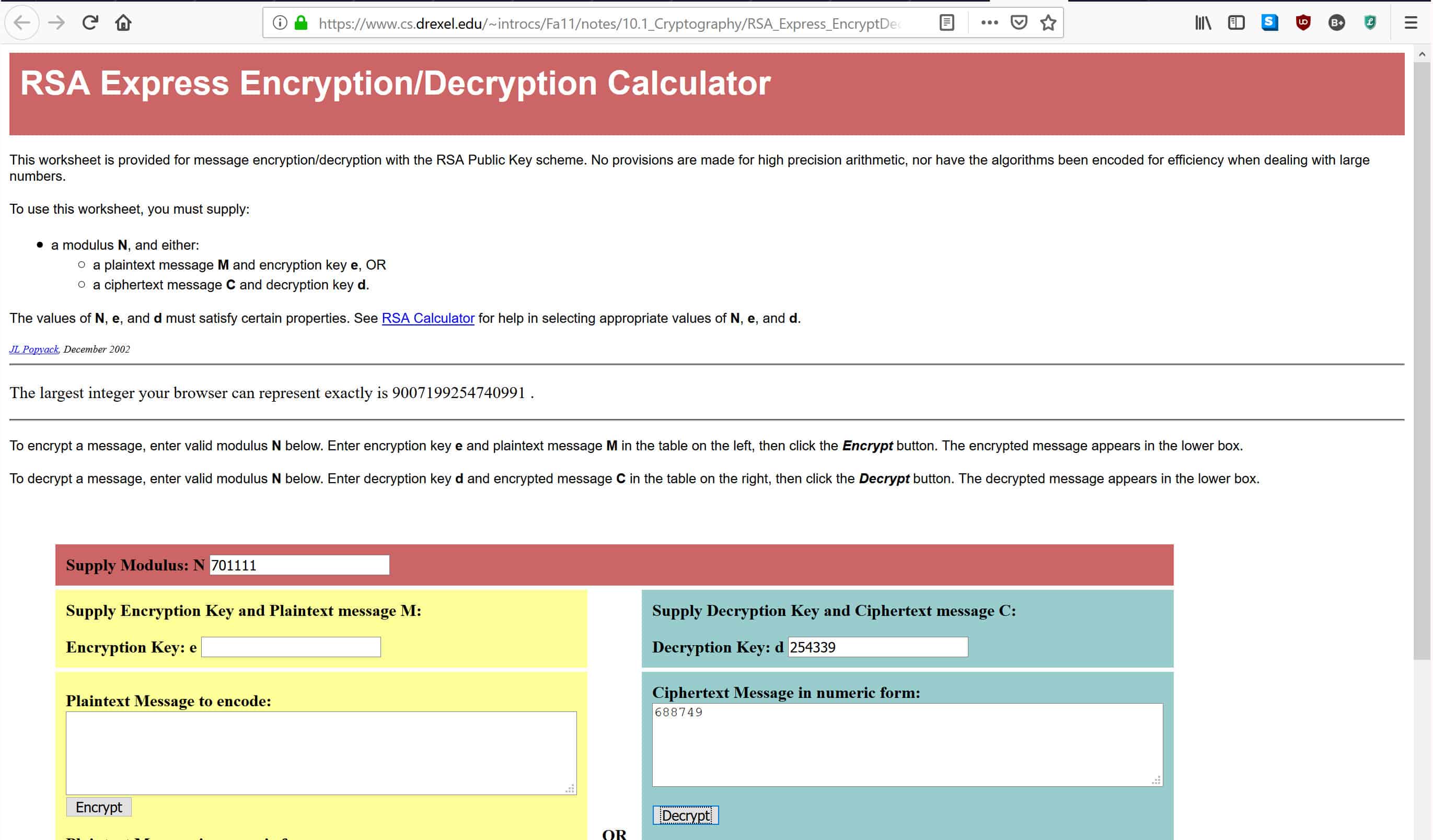
เมื่อคุณป้อนข้อมูลให้กด ถอดรหัส, ซึ่งจะใส่ตัวเลขผ่านสูตรถอดรหัสที่ระบุไว้ข้างต้น นี่จะให้ข้อความต้นฉบับในกล่องด้านล่าง หากคุณทำทุกอย่างถูกต้องคุณควรได้รับคำตอบ 4, ซึ่งเป็นข้อความต้นฉบับที่เราเข้ารหัสด้วยกุญแจสาธารณะของเรา.

การเข้ารหัส RSA ทำงานอย่างไร

ส่วนด้านบนควรให้คุณเข้าใจอย่างสมเหตุสมผลว่าวิธีการทางคณิตศาสตร์ที่อยู่เบื้องหลังการเข้ารหัสคีย์สาธารณะทำงานอย่างไร อาจสร้างความสับสนเล็กน้อย แต่ผู้ที่ไม่เข้าใจความซับซ้อนของสมการสามารถนำข้อมูลสำคัญบางอย่างเกี่ยวกับกระบวนการไปใช้.

ในขั้นตอนข้างต้นเราได้แสดงให้เห็นว่าทั้งสองเอนทิตีสามารถสื่อสารอย่างปลอดภัยได้อย่างไรโดยไม่ต้องแชร์รหัสล่วงหน้ามาก่อน ครั้งแรกพวกเขาแต่ละคนต้อง ตั้งค่าคู่กุญแจของตนเอง และ แบ่งปันกุญแจสาธารณะกับอีกคนหนึ่ง. เอนทิตีทั้งสองต้องเก็บกุญแจส่วนตัวของพวกเขาเป็นความลับเพื่อให้การสื่อสารของพวกเขาปลอดภัย.

เมื่อผู้ส่งมีรหัสสาธารณะของผู้รับพวกเขาสามารถใช้เพื่อเข้ารหัสข้อมูลที่พวกเขาต้องการรักษาความปลอดภัย. เมื่อมันถูกเข้ารหัสด้วยกุญแจสาธารณะมันจะถูกถอดรหัสโดยกุญแจส่วนตัวจากคู่กุญแจเดียวกันเท่านั้น. แม้แต่รหัสสาธารณะอันเดียวกันก็ไม่สามารถใช้ถอดรหัสข้อมูลได้ นี่คือสาเหตุที่คุณสมบัติของ ฟังก์ชั่นประตูกับดัก ที่เรากล่าวถึงข้างต้น.

เมื่อผู้รับได้รับข้อความเข้ารหัสพวกเขาใช้กุญแจส่วนตัวของพวกเขาในการเข้าถึงข้อมูล หากผู้รับต้องการส่งคืนการสื่อสารด้วยวิธีที่ปลอดภัย, พวกเขาสามารถเข้ารหัสข้อความของพวกเขาด้วยกุญแจสาธารณะของบุคคลที่พวกเขากำลังสื่อสารด้วย. อีกครั้งเมื่อมันถูกเข้ารหัสด้วยกุญแจสาธารณะวิธีเดียวที่ข้อมูลนั้นสามารถเข้าถึงได้คือผ่านกุญแจส่วนตัวที่ตรงกัน.

ด้วยวิธีนี้การเข้ารหัส RSA สามารถใช้งานโดยบุคคลที่ไม่รู้จักก่อนหน้านี้เพื่อส่งข้อมูลอย่างปลอดภัยระหว่างกัน ส่วนสำคัญของช่องทางการสื่อสารที่เราใช้ในชีวิตออนไลน์ของเราถูกสร้างขึ้นจากรากฐานนี้.

ข้อความที่ซับซ้อนจะถูกเข้ารหัสด้วย RSA อย่างไร?

ในตัวอย่างของเราเราทำให้สิ่งต่างๆง่ายขึ้นเพื่อให้เข้าใจง่ายขึ้นซึ่งเป็นสาเหตุที่เราเข้ารหัสข้อความของ“ 4” เท่านั้น ความสามารถในการเข้ารหัสหมายเลข 4 ดูเหมือนจะไม่มีประโยชน์อย่างยิ่งดังนั้นคุณอาจสงสัย วิธีที่คุณสามารถเข้ารหัสชุดข้อมูลที่ซับซ้อนมากขึ้น, เช่นคีย์สมมาตร (ซึ่งเป็นการใช้งานทั่วไปของ RSA) หรือแม้แต่ข้อความ.

บางคนอาจงงว่าคีย์เช่น“ n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” หรือข้อความเช่น“ ซื้อฉันแซนวิช” สามารถเข้ารหัสด้วยอัลกอริทึมเช่น RSA ซึ่งเกี่ยวข้องกับตัวเลขและตัวอักษรไม่ได้ ความจริงก็คือข้อมูลทั้งหมดที่กระบวนการคอมพิวเตอร์ของเราจัดเก็บในไบนารี (1s และ 0s) และเราใช้มาตรฐานการเข้ารหัสเช่น ASCII หรือ Unicode เพื่อเป็นตัวแทนของพวกเขาในรูปแบบที่มนุษย์สามารถเข้าใจ (ตัวอักษร).

ซึ่งหมายความว่า แป้นเช่น“ n38cb29fkbjh138g7fqijnf3kaj84f8b9f …” และข้อความเช่น“ ซื้อแซนวิชฉัน” มีอยู่แล้วเป็นตัวเลข, ซึ่งสามารถคำนวณได้ง่ายในอัลกอริธึม RSA ตัวเลขที่พวกเขาแสดงออกมานั้นใหญ่กว่าและยากกว่าสำหรับเราที่จะจัดการซึ่งเป็นสาเหตุที่เราต้องการจัดการกับตัวอักษรและตัวเลขมากกว่าความสับสนของเลขฐานสอง.

หากคุณต้องการ เข้ารหัสเซสชั่นคีย์ที่ยาวขึ้นหรือข้อความที่ซับซ้อนมากขึ้นด้วย RSA มันจะเกี่ยวข้องกับจำนวนที่มากขึ้น.

การขยายความ

เมื่อใช้งาน RSA จะใช้สิ่งที่เรียกว่า padding เพื่อช่วยป้องกันการโจมตีเป็นจำนวนมาก. เพื่ออธิบายวิธีการทำงานเราจะเริ่มด้วยตัวอย่าง สมมติว่าคุณกำลังส่งข้อความรหัสให้เพื่อน:

เรียนชาวกะเหรี่ยง,

    หวังว่าเธอสบายดี. พวกเรายังคงทานอาหารเย็นในวันพรุ่งนี้หรือเปล่า?

    ขอแสดงความนับถือ,

    เจมส์

สมมติว่าคุณเขียนข้อความในวิธีที่ง่ายโดย การเปลี่ยนตัวอักษรแต่ละตัวเป็นตัวอักษรที่ตามมาในตัวอักษร. สิ่งนี้จะเปลี่ยนข้อความเป็น:

Efbs Lbsfo,

    J ipqf zpv bsf xfmm Bsf xf tujmm ibwjoh ejoofs upnpsspx?

    Zpvst tjodfsfmz,

    Kbnft

หากศัตรูของคุณดักจดหมายฉบับนี้มีเคล็ดลับที่พวกเขาสามารถใช้เพื่อลองและถอดรหัสรหัส พวกเขาสามารถ ดูรูปแบบจดหมายของคุณแล้วลองเดาว่าข้อความนั้นอาจพูดอะไร. พวกเขารู้ว่าคนทั่วไปมักเริ่มจดหมายด้วย“ สวัสดี”“ สวัสดี”“ รัก” หรืออนุสัญญาอื่น ๆ.

หากพวกเขาพยายามใช้คำว่า“ สวัสดี” หรือ“ สวัสดี” เป็นคำแรกพวกเขาจะเห็นว่ามันไม่เหมาะกับจำนวนตัวอักษร จากนั้นพวกเขาสามารถลองใช้“ ที่รัก” มันเข้ากันได้ดี แต่นั่นไม่ได้แปลว่าอะไร ผู้โจมตีจะลองและดูว่ามันนำพวกเขาไปที่ไหน ดังนั้นพวกเขาจะเปลี่ยนตัวอักษร “e”, “f”, “b” และ “s” ด้วย “d”, “e”, “a” และ “r” ตามลำดับ สิ่งนี้จะทำให้พวกเขา:

เรียน Laseo,

    J ipqe zpv เป็น xemm มี xe tujmm iawjoh djooes upnpsspx?

    Zpvrt tjoderemz,

    Kanet

มันยังดูสับสนอยู่ดีดังนั้นผู้โจมตีอาจลองดูอนุสัญญาอื่น ๆ, ชอบวิธีที่เราสรุปจดหมายของเรา. ผู้คนมักจะเพิ่ม“ จาก” หรือ“ ขอแสดงความนับถือ” ในตอนท้าย แต่สิ่งเหล่านี้ไม่เหมาะกับรูปแบบ ผู้โจมตีอาจลองใช้ “ของคุณด้วยความจริงใจ” แทนจดหมายอื่นเพื่อดูว่าพวกเขาได้รับจากที่ไหน โดยการเปลี่ยน“ z”,“ p”,“ v”,“ t”,“ j”“ o”,“ d” และ“ m” ด้วย“ y”,“ o”,“ u”,“ s”,“ i”,“ n”,“ c” และ“ l” ตามลำดับพวกเขาจะได้:

เรียนคุณ Lasen,

    ฉัน ioqe คุณเป็น xell xe tuill iawinh dinnes uonossox คือ?

    ขอแสดงความนับถือ,

    Kanet

หลังจากการปรับเปลี่ยนนั้นดูเหมือนว่าผู้โจมตีเริ่มที่จะได้รับที่ไหนสักแห่ง พวกเขาพบคำว่า “ฉัน”, “คุณ” และ “เป็น”, นอกเหนือจากคำที่ประกอบการเดาเริ่มต้นแล้ว.

เมื่อเห็นว่าคำพูดนั้นถูกต้องตามหลักไวยากรณ์ที่ถูกต้องผู้โจมตีสามารถมั่นใจได้ว่าพวกเขากำลังมุ่งหน้าไปในทิศทางที่ถูกต้อง โดยตอนนี้พวกเขาอาจจะตระหนักว่ารหัสที่เกี่ยวข้องกับตัวอักษรแต่ละตัวจะถูกเปลี่ยนเป็นตัวอักษรที่ตามมาในตัวอักษร. เมื่อพวกเขาตระหนักถึงสิ่งนี้ทำให้การแปลที่เหลือเป็นเรื่องง่ายและอ่านข้อความต้นฉบับ.

ตัวอย่างข้างต้นเป็นเพียงรหัสง่ายๆ แต่อย่างที่คุณเห็น, โครงสร้างของข้อความสามารถให้เบาะแสผู้โจมตีเกี่ยวกับเนื้อหา. แน่นอนว่ามันยากที่จะเข้าใจข้อความจากเพียงแค่โครงสร้างและใช้การคาดเดาที่มีการศึกษา แต่คุณต้องจำไว้ว่าคอมพิวเตอร์ทำสิ่งนี้ได้ดีกว่าเรา. ซึ่งหมายความว่าสามารถใช้เพื่อหารหัสที่ซับซ้อนมากขึ้นในเวลาที่สั้นลง, ขึ้นอยู่กับเบาะแสที่มาจากโครงสร้างและองค์ประกอบอื่น ๆ.

หากโครงสร้างสามารถนำไปสู่โค้ดที่ถอดรหัสและเปิดเผยเนื้อหาของข้อความเราจำเป็นต้องมีวิธีการซ่อนโครงสร้างเพื่อรักษาความปลอดภัยของข้อความ สิ่งนี้ทำให้เรา การขยายความ.

เมื่อข้อความมีเบาะ, มีการเพิ่มข้อมูลแบบสุ่มเพื่อซ่อนร่องรอยการจัดรูปแบบดั้งเดิมซึ่งอาจนำไปสู่ข้อความที่เข้ารหัสซึ่งใช้งานไม่ได้. ด้วย RSA สิ่งต่าง ๆ มีความซับซ้อนเล็กน้อยเนื่องจากคีย์เข้ารหัสไม่มีการจัดรูปแบบที่ชัดเจนของตัวอักษรที่ช่วยให้เรามีเงื่อนงำในตัวอย่างข้างต้น.

ฝ่ายตรงข้ามสามารถใช้การโจมตีจำนวนหนึ่งเพื่อใช้ประโยชน์จากคุณสมบัติทางคณิตศาสตร์ของรหัสและทำลายข้อมูลที่เข้ารหัส เนื่องจากภัยคุกคามนี้, การใช้งานของ RSA ใช้รูปแบบการขยายเช่น OAEP เพื่อฝังข้อมูลพิเศษลงในข้อความ. การเพิ่มการขยายนี้ก่อนที่ข้อความจะถูกเข้ารหัสทำให้ RSA ปลอดภัยยิ่งขึ้น.

การเซ็นข้อความ

RSA สามารถใช้งานได้มากกว่าการเข้ารหัสข้อมูล คุณสมบัติของมันยังทำให้มันเป็นระบบที่มีประโยชน์สำหรับ ยืนยันว่าข้อความถูกส่งโดยองค์กรที่อ้างว่าได้ส่งข้อความดังกล่าวรวมถึงการพิสูจน์ว่าข้อความนั้นไม่ได้รับการแก้ไขหรือดัดแปลง.

เมื่อมีคนต้องการที่จะพิสูจน์ความถูกต้องของข้อความของพวกเขาพวกเขาสามารถคำนวณ กัญชา (ฟังก์ชั่นที่รับข้อมูลขนาดที่กำหนดเองแล้วเปลี่ยนเป็นค่าความยาวคงที่) ของข้อความธรรมดาแล้วเซ็นชื่อด้วยรหัสส่วนตัวของพวกเขา พวกเขา เซ็นชื่อแฮชโดยใช้สูตรเดียวกันกับที่ใช้ในการถอดรหัส (m = cd mod n) เมื่อข้อความได้รับการลงนามพวกเขาส่งลายเซ็นดิจิตอลนี้ไปยังผู้รับพร้อมข้อความ.

หากผู้รับได้รับข้อความที่มีลายเซ็นดิจิทัลพวกเขาสามารถใช้ ลายเซ็นเพื่อตรวจสอบว่าข้อความได้รับการลงนามโดยกุญแจส่วนตัวของบุคคลที่อ้างว่าได้ส่ง. พวกเขายังสามารถดูว่าข้อความถูกเปลี่ยนแปลงโดยผู้โจมตีหลังจากที่ถูกส่ง.

ในการตรวจสอบลายเซ็นดิจิทัลผู้รับจะใช้ฟังก์ชันแฮชเดียวกันก่อนเพื่อค้นหาค่าแฮชของข้อความที่ได้รับ จากนั้นผู้รับใช้ กุญแจสาธารณะของผู้ส่ง เพื่อลายเซ็นดิจิตอล, ใช้สูตรการเข้ารหัส (c = mอี mod n), เพื่อให้แฮชของลายเซ็นดิจิทัล.

โดย เปรียบเทียบแฮชของข้อความที่ได้รับพร้อมกับแฮชจากลายเซ็นดิจิตอลที่เข้ารหัส, ผู้รับสามารถบอกได้ว่าข้อความนั้นเป็นของแท้หรือไม่. หากทั้งสองค่าเหมือนกันข้อความจะไม่ถูกเปลี่ยนตั้งแต่ลงนาม โดยผู้ส่งต้นฉบับ หากข้อความได้รับการแก้ไขโดยแม้แต่อักขระเดียวค่าแฮชจะแตกต่างกันโดยสิ้นเชิง.

ความปลอดภัย RSA & การโจมตี

เช่นเดียวกับ cryptosystems ส่วนใหญ่ความปลอดภัยของ RSA ขึ้นอยู่กับวิธีการนำไปใช้และการใช้งาน ปัจจัยหนึ่งที่สำคัญคือขนาดของกุญแจ ยิ่งจำนวนของบิตในคีย์มากขึ้น (โดยหลักจะใช้เวลานานแค่ไหนในการคีย์) ยิ่งยากที่จะถอดรหัสผ่านการโจมตี เช่นเดรัจฉานบังคับและแฟ.

เนื่องจากอัลกอริธึมที่ไม่สมมาตรของคีย์เช่น RSA สามารถถูกทำลายได้ด้วยการแยกตัวประกอบจำนวนเต็มในขณะที่อัลกอริธึมของคีย์ที่สมมาตรเช่น AES ไม่สามารถทำได้คีย์ RSA จะต้องใช้เวลานานกว่ามากในการรักษาความปลอดภัยระดับเดียวกัน.

ปัจจุบัน ขนาดคีย์ที่ใหญ่ที่สุดที่ได้รับการแฟ็กเตอริ่งคือ 768 บิต. สิ่งนี้ทำโดยทีมงานวิชาการในช่วงเวลาสองปีโดยใช้เครื่องจักรหลายร้อยเครื่อง.

เนื่องจากแฟคตอริ่งเสร็จสมบูรณ์ภายในสิ้นปี 2009 และพลังการประมวลผลได้เพิ่มขึ้นอย่างมากตั้งแต่นั้นมาจึงสามารถสันนิษฐานได้ว่าความพยายามของความเข้มที่คล้ายกัน สามารถแยกคีย์ RSA ที่ใหญ่กว่านี้ได้แล้ว.

อย่างไรก็ตามเรื่องนี้เวลาและทรัพยากรที่จำเป็นสำหรับการโจมตีประเภทนี้ทำให้พ้นแฮ็กเกอร์ส่วนใหญ่และเข้าสู่อาณาจักรของรัฐ ความยาวคีย์ที่ดีที่สุดที่จะใช้จะขึ้นอยู่กับรุ่นภัยคุกคามส่วนบุคคลของคุณ สถาบันมาตรฐานและเทคโนโลยีแห่งชาติ แนะนำขนาดหลักขั้นต่ำของ 2048 บิต, แต่ก็ใช้คีย์ 4096 บิต ในบางสถานการณ์ที่ระดับการคุกคามสูงขึ้น.

แฟคตอริ่งเป็นเพียงหนึ่งวิธีที่ RSA สามารถถูกทำลายได้ การโจมตีอื่น ๆ จำนวนมากมีแนวโน้มที่จะทำลายการเข้ารหัสด้วยทรัพยากรจำนวนน้อย แต่สิ่งเหล่านี้ขึ้นอยู่กับการใช้งานและปัจจัยอื่น ๆ ซึ่งไม่จำเป็นต้องเป็น RSA บางส่วนของเหล่านี้รวมถึง:

เป็นช่วงเวลาที่สุ่มสุ่มจริงๆ?

การใช้งานบางอย่างของ RSA ใช้ตัวสร้างตัวเลขสุ่มที่อ่อนแอเพื่อให้ได้จำนวนเฉพาะ หากตัวเลขเหล่านี้ไม่ได้สุ่มอย่างเพียงพอจะทำให้ผู้โจมตีแยกแยะได้ง่ายขึ้นและทำลายการเข้ารหัส ปัญหานี้ สามารถหลีกเลี่ยงได้โดยใช้ตัวสร้างตัวเลขสุ่มหลอกแบบเข้ารหัสลับที่ปลอดภัย.

การสร้างคีย์ไม่ดี

คีย์ RSA ต้องอยู่ในพารามิเตอร์ที่กำหนดเพื่อความปลอดภัย. ถ้ามีเฉพาะช่วงเวลา พี และ Q อยู่ใกล้กันเกินไปกุญแจสามารถค้นพบได้ง่าย. ในทำนองเดียวกันจำนวน d ที่ทำให้ส่วนหนึ่งของคีย์ส่วนตัวต้องไม่เล็กเกินไป. ค่าต่ำทำให้ง่ายต่อการแก้ไข สิ่งสำคัญคือหมายเลขเหล่านี้มีความยาวเพียงพอที่จะทำให้กุญแจของคุณปลอดภัย.

การโจมตีช่องทางด้านข้าง

นี่เป็นประเภทของการโจมตีที่จะไม่ทำลาย RSA โดยตรง แต่ควรใช้ข้อมูลจากการนำไปปฏิบัติเพื่อให้คำแนะนำแก่ผู้โจมตีเกี่ยวกับกระบวนการเข้ารหัส การโจมตีเหล่านี้อาจรวมถึงสิ่งต่าง ๆ เช่น การวิเคราะห์ปริมาณพลังงานที่ใช้, หรือ การวิเคราะห์การทำนายสาขา, ซึ่งใช้การวัดเวลาดำเนินการเพื่อค้นหาคีย์ส่วนตัว.

การโจมตีช่องทางอีกประเภทหนึ่งเรียกว่าการโจมตีแบบกำหนดเวลา หากผู้โจมตีมีความสามารถในการวัดเวลาถอดรหัสในคอมพิวเตอร์เป้าหมายของพวกเขาสำหรับจำนวนข้อความเข้ารหัสที่แตกต่างกัน, ข้อมูลนี้สามารถทำให้ผู้โจมตีสามารถตรวจสอบคีย์ส่วนตัวของเป้าหมายได้.

การใช้งานส่วนใหญ่ของ RSA หลีกเลี่ยงการโจมตีนี้โดยการเพิ่มค่าครั้งเดียวในระหว่างกระบวนการเข้ารหัสซึ่งจะลบความสัมพันธ์นี้ กระบวนการนี้เรียกว่า ทำให้ไม่เห็นการเข้ารหัสลับ.

การเข้ารหัส RSA ปลอดภัยสำหรับอนาคตหรือไม่?

ข่าวดีก็คือว่า RSA นั้นปลอดภัยสำหรับการใช้งานแม้จะมีการโจมตีที่เป็นไปได้ ข้อแม้คือ จำเป็นต้องดำเนินการอย่างถูกต้องและใช้คีย์ที่อยู่ภายในพารามิเตอร์ที่ถูกต้อง. ดังที่เราได้กล่าวไปแล้วการใช้งานที่ไม่ใช้การขยายใช้ช่วงเวลาที่ไม่เหมาะสมหรือมีช่องโหว่อื่น ๆ ไม่สามารถพิจารณาได้ว่าปลอดภัย.

หากคุณต้องการใช้การเข้ารหัส RSA, ตรวจสอบให้แน่ใจว่าคุณกำลังใช้คีย์อย่างน้อย 1024 บิต. ผู้ที่มีรูปแบบการคุกคามที่สูงกว่าควรยึดติดกับคีย์ของ 2048 หรือ 4096 บิตหากพวกเขาต้องการใช้ RSA ด้วยความมั่นใจ ตราบใดที่คุณตระหนักถึงจุดอ่อนที่ RSA มีและใช้อย่างถูกต้องคุณควรรู้สึกปลอดภัยที่จะใช้ RSA สำหรับการแชร์คีย์และงานอื่น ๆ ที่คล้ายกันซึ่งต้องการการเข้ารหัสคีย์สาธารณะ.

ดูสิ่งนี้ด้วย: อธิบายประเภทการเข้ารหัสทั่วไป